Entrar Página Discusión Historial Go to the site toolbox

Fusión de hielo en un recipiente

De Laplace

(Diferencias entre revisiones)
(→Superficie de contacto)
Línea 28: Línea 28:
En resumen, tal como se explicó en clase:
En resumen, tal como se explicó en clase:
-
:''Eel nivel del agua con hielo flotando no cambia cuando el hielo se derrite y es igual al que habría si toda el agua fuera líquida.''
+
:''El nivel del agua con hielo flotando no cambia cuando el hielo se derrite y es igual al que habría si toda el agua fuera líquida.''
Si tenemos que el agua ocupa un volumen de 1000 cm³ la altura a la que llega la obtenemos dividiendo por el área
Si tenemos que el agua ocupa un volumen de 1000 cm³ la altura a la que llega la obtenemos dividiendo por el área
Línea 37: Línea 37:
Una vez que tenemos la altura a la que llega el área, calculamos la superficie de contacto como la suma de la base (un círculo) + más la cara lateral (un rectángulo), lo que nos da
Una vez que tenemos la altura a la que llega el área, calculamos la superficie de contacto como la suma de la base (un círculo) + más la cara lateral (un rectángulo), lo que nos da
-
<center><math>A = \pi r^2 + 2\pi r h \simeq 450\,\mathrm{cm}^2</math></center>
+
<center><math>A = \pi r^2 + 2\pi r h \simeq 451\,\mathrm{cm}^2</math></center>
===Flujo de calor===
===Flujo de calor===
-
 
+
El calor entra en el sistema desde el baño por conducción:
-
==Flujo de calor==
+
-
Podemos obtener la cantidad de calor que entra por segundo a partir de la expresión para la conducción de calor
+
<center><math>\dot{Q}=k A\frac{\Delta T}{\Delta x}</math></center>
<center><math>\dot{Q}=k A\frac{\Delta T}{\Delta x}</math></center>
-
 
-
En este caso A es el área lateral del recipiente. Este área es la de la base, más la parte de cara lateral hasta la altura a la que llega el agua. hallamos primero esta altura
 
-
 
-
<center><math>h = \frac{V}{\pi a^2}=\frac{1000\,\mathrm{cm}^3}{\pi (8\,\mathrm{cm})^2} = 4.97\,\mathrm{cm}</math></center>
 
-
 
-
Nótese que no hace falta distinguir entre agua e hielo, ya que por tratarse de la misma sustancia, el principio de Arquímedes nos dice que el volumen desalojado de agua por 0.5&thinsp;kg de hielo es justamente 0.5 litros.
 
-
 
-
La superficie de agua en contacto con el vidrio es
 
-
 
-
<center><math>A = \pi r^2 + 2\pi r h = \pi r (2+h) = 0.0451\,\mathrm{m}^2</math></center>
 
En la expresión del flujo de calor <math>\Delta T</math> la diferencia de temperaturas entre las dos caras (20&thinsp;K) y <math>\Delta x</math> el espesor del recipiente (0.01&thinsp;m). Por tanto
En la expresión del flujo de calor <math>\Delta T</math> la diferencia de temperaturas entre las dos caras (20&thinsp;K) y <math>\Delta x</math> el espesor del recipiente (0.01&thinsp;m). Por tanto
Línea 60: Línea 48:
<center><math>\dot{Q}=1.1\,\frac{\mathrm{W}}{\mathrm{K}\cdot\mathrm{m}}\times 0.0451\mathrm{m}^2\times \frac{20\,\mathrm{K}}{0.01\,\mathrm{m}} = 99.2\,\mathrm{W}</math></center>
<center><math>\dot{Q}=1.1\,\frac{\mathrm{W}}{\mathrm{K}\cdot\mathrm{m}}\times 0.0451\mathrm{m}^2\times \frac{20\,\mathrm{K}}{0.01\,\mathrm{m}} = 99.2\,\mathrm{W}</math></center>
-
==Hielo fundido por segundo==
+
==Fusión del hielo==
 +
===Hielo fundido por segundo===
La cantidad de hielo que se funde por segundo la hallamos dividiendo la cantidad de calor que entra en este tiempo por la cantidad de calor necesaria para fundir un kilogramo de hielo
La cantidad de hielo que se funde por segundo la hallamos dividiendo la cantidad de calor que entra en este tiempo por la cantidad de calor necesaria para fundir un kilogramo de hielo
<center><math>\dot{m}=\frac{\dot{Q}}{\Delta h_f}=\frac{99.23\,\mathrm{W}}{333.55\,\mathrm{kJ}/\mathrm{kg}}=0.298\,\frac{\mathrm{g}}{\mathrm{s}}</math></center>
<center><math>\dot{m}=\frac{\dot{Q}}{\Delta h_f}=\frac{99.23\,\mathrm{W}}{333.55\,\mathrm{kJ}/\mathrm{kg}}=0.298\,\frac{\mathrm{g}}{\mathrm{s}}</math></center>
 +
===Tiempo total de fusión===
A este ritmo se necesita un tiempo
A este ritmo se necesita un tiempo
<center><math>T = \frac{M}{\dot{m}}= \frac{500\,\mathrm{g}}{0.298\,\mathrm{g}/\mathrm{s}} = 1680\,\mathrm{s}=28\,\mathrm{min}</math></center>
<center><math>T = \frac{M}{\dot{m}}= \frac{500\,\mathrm{g}}{0.298\,\mathrm{g}/\mathrm{s}} = 1680\,\mathrm{s}=28\,\mathrm{min}</math></center>
 +
para fundir el hielo por completo. La cantidad de calor que entra en ese tiempo es
 +
 +
<center><math>\dot{Q}T = M\,\Delta h_f = 167\,\mathrm{kJ}</math></center>
==Variación de entropía==
==Variación de entropía==
En este problema tenemos una variación de entropía en el agua/hielo y otra en el ambiente. Ambas ocurren a temperatura constante y de forma reversible
En este problema tenemos una variación de entropía en el agua/hielo y otra en el ambiente. Ambas ocurren a temperatura constante y de forma reversible

Revisión de 16:54 22 jun 2010

Contenido

1 Enunciado

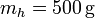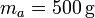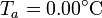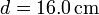Se tiene un bloque de hielo de masa m_h = 500\,\mathrm{g} de hielo sumergido en un volumen de agua de masa m_a = 500\,\mathrm{g}, ambos a una temperatura T_a = 0.00 ^\circ\mathrm{C} . El conjunto está contenido en un recipiente cilíndrico de vidrio, de diámetro d = 16.0\,\mathrm{cm} y espesor 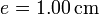e = 1.00\,\mathrm{cm}, abierto por arriba al aire (que se puede suponer un aislante térmico perfecto). 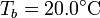El recipiente está sumergido en un baño de agua a T_b = 20.0 ^\circ \mathrm{C}.

  1. Calcula la superficie de agua en contacto con el recipiente y la cantidad de calor que entra en él en 1.00 s.
  2. Halla la cantidad de hielo que se funde en el mismo tiempo. ¿Cuánto tiempo tardará en derretirse por completo?
  3. Calcula la variación de entropía en el sistema, en el ambiente y la variación de entropía total en la fusión completa del hielo.
  4. Supón que en lugar de permitir que el calor fluya directamente desde el baño al sistema se hace pasar por una máquina térmica reversible que opera entre las dos temperaturas. ¿Qué trabajo puede producirse hasta que el hielo se funde completamente? ¿Cuánto calor sale del baño en ese caso? Calcula la variación de entropía del Universo en este proceso.

Datos: Densidad de masa del agua líquida 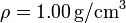\rho = 1.00\,\mathrm{g}/\mathrm{cm}^3; Conductividad térmica del vidrio 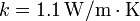k= 1.1\,\mathrm{W}/\mathrm{m}\cdot\mathrm{K}; Entalpía específica de fusión: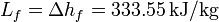 L_f = \Delta h_f = 333.55\,\mathrm{kJ}/\mathrm{kg}

2 Flujo de calor

2.1 Altura del agua

La altura a la que llega el agua la obtenemos por simple aplicación del principio de Arquímedes. Tenemos 500 g de agua, que ocupan 500 cm³, y 500 g de hielo.

Este trozo de hielo desaloja una cantidad de agua que pesa 500 g (pues el hielo está en equilibrio y su peso se compensa por el empuje del agua). El volumen correspondiente al agua desalojada será por tanto 500 cm³ y el volumen total de agua más volumen desalojado es

500 cm³ + 500 cm³ = 1000 cm³

A medida que el hielo se derrita, ¿el nivel de agua subirá o bajará? Ninguna de las dos cosas.

Supongamos que se ha derretido parcialmente y en un momento dado quedan 200 g de hielo. Los 300 g restantes se habrán convertido en agua, con lo que ahora tendremos 800 g de agua. Por su parte, los 200 g de hielo restante desalojan 200 g de agua, que ocupan 200 cm³, con lo que el volumen total es

800 cm³ + 200 cm³ = 1000 cm³

Obviamente, cuando el hielo se funda por completo, tendremos 1000 g de agua que ocupan 1000 cm³.

En resumen, tal como se explicó en clase:

El nivel del agua con hielo flotando no cambia cuando el hielo se derrite y es igual al que habría si toda el agua fuera líquida.

Si tenemos que el agua ocupa un volumen de 1000 cm³ la altura a la que llega la obtenemos dividiendo por el área

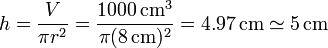
h = \frac{V}{\pi r^2}=\frac{1000\,\mathrm{cm}^3}{\pi (8\,\mathrm{cm})^2}=4.97\,\mathrm{cm}\simeq 5\,\mathrm{cm}

2.2 Superficie de contacto

Una vez que tenemos la altura a la que llega el área, calculamos la superficie de contacto como la suma de la base (un círculo) + más la cara lateral (un rectángulo), lo que nos da

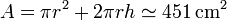
A = \pi r^2 + 2\pi r h \simeq 451\,\mathrm{cm}^2

2.3 Flujo de calor

El calor entra en el sistema desde el baño por conducción:

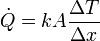
\dot{Q}=k A\frac{\Delta T}{\Delta x}

En la expresión del flujo de calor ΔT la diferencia de temperaturas entre las dos caras (20 K) y Δx el espesor del recipiente (0.01 m). Por tanto

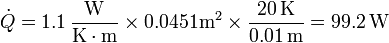
\dot{Q}=1.1\,\frac{\mathrm{W}}{\mathrm{K}\cdot\mathrm{m}}\times 0.0451\mathrm{m}^2\times \frac{20\,\mathrm{K}}{0.01\,\mathrm{m}} = 99.2\,\mathrm{W}

3 Fusión del hielo

3.1 Hielo fundido por segundo

La cantidad de hielo que se funde por segundo la hallamos dividiendo la cantidad de calor que entra en este tiempo por la cantidad de calor necesaria para fundir un kilogramo de hielo

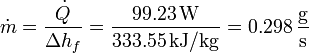
\dot{m}=\frac{\dot{Q}}{\Delta h_f}=\frac{99.23\,\mathrm{W}}{333.55\,\mathrm{kJ}/\mathrm{kg}}=0.298\,\frac{\mathrm{g}}{\mathrm{s}}

3.2 Tiempo total de fusión

A este ritmo se necesita un tiempo

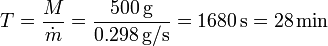
T = \frac{M}{\dot{m}}= \frac{500\,\mathrm{g}}{0.298\,\mathrm{g}/\mathrm{s}} = 1680\,\mathrm{s}=28\,\mathrm{min}

para fundir el hielo por completo. La cantidad de calor que entra en ese tiempo es

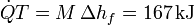
\dot{Q}T = M\,\Delta h_f = 167\,\mathrm{kJ}

4 Variación de entropía

En este problema tenemos una variación de entropía en el agua/hielo y otra en el ambiente. Ambas ocurren a temperatura constante y de forma reversible

4.1 Variación en el agua

La variación de entropía por segundo será

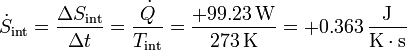
\dot{S}_\mathrm{int}= \frac{\Delta S_\mathrm{int}}{\Delta t} = \frac{\dot{Q}}{T_\mathrm{int}}= \frac{+99.23\,\mathrm{W}}{273\,\mathrm{K}}=+0.363\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{s}}

Esta variación es positiva, como corresponde a que esté aumentando el desorden en el sistema, al pasar de sólido a líquido.

4.2 Variación en el ambiente

En el ambiente tenemos una salida de calor (que va al recipiente). La variación de entropía por segundo será

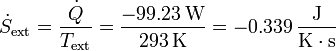
\dot{S}_\mathrm{ext}= \frac{\dot{Q}}{T_\mathrm{ext}}= \frac{-99.23\,\mathrm{W}}{293\,\mathrm{K}}=-0.339\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{s}}

4.3 Variación neta

Sumando ambas variaciones

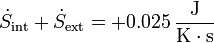
\dot{S}_\mathrm{int}+\dot{S}_\mathrm{ext} = +0.025\,\frac{\mathrm{J}}{\mathrm{K}\cdot\mathrm{s}}

la variación es positiva, lo que quiere decir que el proceso es posible e irreversible.

El problema puede aparecer a la hora de ubicar esta producción de entropía. Si el combinado agua/hielo recibe de calor de forma reversible (pues lo hace a temperatura constante) y el baño térmico lo cede también de forma isoterma y reversible, ¿dónde está la irreversibilidad que implica este aumento de entropía?

La respuesta es el único sitio que no se ha considerado: el recipiente. Éste no es solo una frontera ideal. Es un sistema en sí mismo, que toma calor a una temperatura (293 K) y lo cede a una inferior (273 K), siendo la producción de entropía correspondiente la que acabamos de calcular.

Obtenido de "http://tesla.us.es/wiki/index.php/Fusi%C3%B3n_de_hielo_en_un_recipiente"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace