Espira cuadrada en campo no uniforme
De Laplace
(Diferencias entre revisiones)
(→Corriente inducida) |
(→Corriente inducida) |
||
| Línea 24: | Línea 24: | ||
En este caso | En este caso | ||
| - | <center><math>\Phi_m = \int_{-a/2}^{a/2}\int_{v_0t}^{v_0t+a}(Cx^2\mathbf{u}_z)\cdot(\mathrm{d}x\,\mathrm{d}y\,\mathbf{u}_z)= | + | <center><math>\Phi_m = \int_{-a/2}^{a/2}\int_{v_0t}^{v_0t+a}(Cx^2\mathbf{u}_z)\cdot(\mathrm{d}x\,\mathrm{d}y\,\mathbf{u}_z)= </math></center> |
==Fuerza magnética== | ==Fuerza magnética== | ||
Revisión de 11:58 12 jun 2010
Contenido |
1 Enunciado
En una región del espacio existe un campo magnético

Una espira cuadrada de lado a y resistencia R se encuentra situada en el plano z = 0 con sus lados paralelos a los ejes. La espira se mueve de forma que su extremo trasero se encuentra en la posición x = v0t.
- Calcule la corriente que circula por la espira.
- Halle la fuerza que el campo magnético ejerce sobre la espira.
- Calcule la potencia disipada en la espira y la energía total disipada durante un tiempo T.
2 Corriente inducida
La corriente que circula por la espira se calcula por aplicación de la ley de Faraday
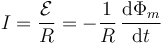
Calculamos el flujo magnético a través de un cuadrado apoyado en la espira. Asignamos un sentido de recorrido antihorario para la corriente, de forma que la normal a la superficie sobre la que calculamos el flujo va en la dirección de  .
.
El campo magnético en todos los puntos de esta superficie vale
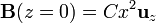
En este caso