Frenado de espira cuadrada
De Laplace
(→Cálculo de la corriente) |
(→Cálculo de la fuerza) |
||
| Línea 26: | Línea 26: | ||
===Cálculo de la fuerza=== | ===Cálculo de la fuerza=== | ||
| + | Al circular una corriente por la espira y encontrarse ésta en el seno de un campo magnético, aparece una fuerza sobre la espira, dada por la ley de Lorentz para una corriente | ||
| + | |||
| + | <center><math\mathbf{F}=I\oint \mathrm{d}\mathbf{r}\times\mathbf{B}</math></center> | ||
| + | |||
| + | En este caso el campo magnético ejerce fuerza sobre tres de los lados, por estar el cuarto en el exterior. Asimismo, las fuerzas sobre los lados superior e inferior se cancelan, por ser iguales y opuestas. Queda la fuerza sobre la barra frontal, para la cual tenemos | ||
| + | |||
| + | <center><math\mathbf{F}=I\int \mathrm{d}\mathbf{r}\times\mathbf{B} = I\int_0^a \left(\mathrm{d}y\mathbf{u}_y\right)\times\left(B_0\mathbf{u}_z\right)= IaB_0\bu{x}</math></center> | ||
| + | |||
| + | Sustituyendo el valor de la corriente | ||
| + | |||
| + | <center><math>\mathbf{F}=-\frac{a^2B_0^2v}{R}\mathbf{u}_x=-\frac{a^2B_0^2}{R}\mathbf{v}</math></center> | ||
| + | |||
| + | Resulta una fuerza opuesta a la velocidad y proporcional a ella. Esta fuerza tiende a frenar la espira, funcionando como una fuerza de rozamiento viscoso. | ||
| + | |||
===Energía y potencia disipada=== | ===Energía y potencia disipada=== | ||
===Frenado magnético=== | ===Frenado magnético=== | ||
[[Categoría:Problemas de inducción electromagnética]] | [[Categoría:Problemas de inducción electromagnética]] | ||
Revisión de 09:59 25 may 2008
Contenido |
1 Enunciado
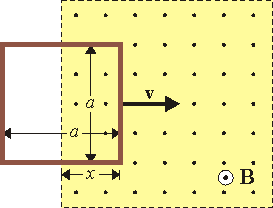
Una espira cuadrada de lado , hecha de un hilo de cobre de sección
, hecha de un hilo de cobre de sección 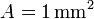 penetra en un campo magnético uniforme perpendicular al plano de la espira y de módulo
penetra en un campo magnético uniforme perpendicular al plano de la espira y de módulo 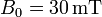 . La espira se mueve inicialmente con velocidad
. La espira se mueve inicialmente con velocidad 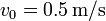 tangente a uno de sus lados y perpendicular al campo magnético. En t = 0 la espira entra en el campo.
tangente a uno de sus lados y perpendicular al campo magnético. En t = 0 la espira entra en el campo.
- Calcule la corriente que se induce en la espira cuando la espira ha avanzado una distancia
 y se está moviendo con velocidad
y se está moviendo con velocidad  .
.
- Halle la fuerza que el campo magnético ejerce con la espira.
- Si la velocidad de la espira se mantiene constante, halle la potencia disipada en la espira por efecto Joule. ¿De dónde proviene la energía disipada?
- Si se deja que la espira frene por acción del campo magnético, determine la evolución en el tiempo de la velocidad, así como la energía total disipada por efecto Joule.
2 Solución
2.1 Cálculo de la corriente
Como en otros problemas, obtenemos la corriente hallando la fuerza electromotriz por aplicación de la ley de Faraday y posteriormente calculamos la corriente aplicando la ley de ohm para un circuito.
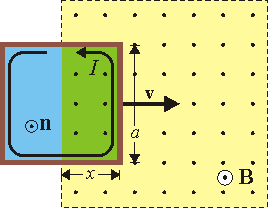
Suponemos un sentido de recorrido tal que la normal a la superficie apoyada en la curva va en el mismo sentido que el campo magnético. En esta superficie el flujo magnético es igual a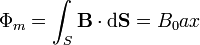
ya que aunque la espira es cuadrada, sólo el rectángulo de base a y altura x se encuentra dentro del campo magnético. La fuerza electromotriz en la espira es
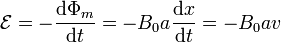
y la corriente que circula por ella

Vemos que, si la espira está entrando en el campo magnético, el sentido de la corriente es el contrario del que habíamos supuesto. Esto está de acuerdo con la ley de Lenz, pues la corriente inducida debe producir un flujo negativo para reducir el aumento del flujo magnético.
2.2 Cálculo de la fuerza
Al circular una corriente por la espira y encontrarse ésta en el seno de un campo magnético, aparece una fuerza sobre la espira, dada por la ley de Lorentz para una corriente
En este caso el campo magnético ejerce fuerza sobre tres de los lados, por estar el cuarto en el exterior. Asimismo, las fuerzas sobre los lados superior e inferior se cancelan, por ser iguales y opuestas. Queda la fuerza sobre la barra frontal, para la cual tenemos
Sustituyendo el valor de la corriente

Resulta una fuerza opuesta a la velocidad y proporcional a ella. Esta fuerza tiende a frenar la espira, funcionando como una fuerza de rozamiento viscoso.