Teoremas de conservación para una partícula
De Laplace
(→Constantes dependientes del tiempo) |
(→Constantes de movimiento) |
||
| Línea 13: | Línea 13: | ||
<center><math>C(\mathbf{r},\mathbf{v})=C(\mathbf{r}_0,\mathbf{v}_0)\,</math></center> | <center><math>C(\mathbf{r},\mathbf{v})=C(\mathbf{r}_0,\mathbf{v}_0)\,</math></center> | ||
| + | |||
| + | Las integrales primeras pueden tener una interpretación física directa (como la energía o el momento cinético) o ser combinaciones más o menos abstractas válidas para un solo problema concreto. Por ejemplo, en el movimiento planetario se conserva el llamado vector de Laplace-Runge-Lenz, que carece de interpretación sencilla. | ||
===Constantes dependientes del tiempo=== | ===Constantes dependientes del tiempo=== | ||
Revisión de 11:36 12 feb 2010
Contenido |
1 Constantes de movimiento
Una constante de movimiento o integral primera es una magnitud función de la posición, velocidad de la partícula (o de las partículas, si hay más de una), cuyo valores constante en el tiempo, pese a que la posición y la velocidad si son variables en el tiempo
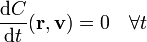
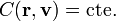
El ejemplo más intuitivo, que veremos más adelante, es el de la energía mecánica. Cuando un cuerpo cae, su posición varía y su velocidad aumenta, pero la energía mecánica, que es una cierta combinación de la posición y la velocidad, permanece constante.
Se denominan también integrales primeras, porque estas cantidades suelen obtenerse integrando una vez las ecuaciones de movimiento.
El hallazgo de una constante de movimiento en un problema simplifica la solución de éste, ya que permite establecer relaciones entre las variables y limita el número de soluciones posibles.
El valor concreto de una constante de movimiento puede calcularse a partir de las condiciones iniciales (o de los valores de la posicióin y velocidad en cualquier instante)
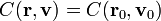
Las integrales primeras pueden tener una interpretación física directa (como la energía o el momento cinético) o ser combinaciones más o menos abstractas válidas para un solo problema concreto. Por ejemplo, en el movimiento planetario se conserva el llamado vector de Laplace-Runge-Lenz, que carece de interpretación sencilla.
1.1 Constantes dependientes del tiempo
Más en general, pueden encontrarse constantes de movimiento que además de la posición y velocidad, dependen del tiempo
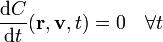
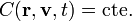
Su valor concreto lo da de nuevo la evaluación en un instante concreto
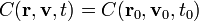
Puede parecer raro que se diga que una cantidad función del tiempo no depende del tiempo. Lo que se afirma es que aunque en la función puede aparecer la variable t, el valor de la función es constante.
Por ejemplo, consideremos el caso de una partícula libre (que se moverá en un movimiento rectilíneo y uniforme)
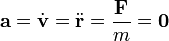
En este caso, la velocidad es una constante de movimiento
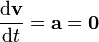
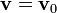
Si ahora construimos la cantidad vectorial, función del tiempo,
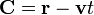
donde 
y 
son las velocidades instantáneas. ¿Cuánto vale su derivada respecto al tiempo?
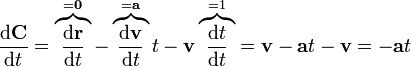
Para una partícula libre la aceleración es nula, así que
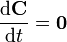
y por tanto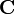 
tiene siempre el mismo valor, aunque sea una función del tiempo. Hallamos este valor a partir de las condiciones iniciales.
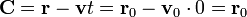
Y ahora, una vez que tenemos las dos constantes de movimiento, podemos depejar y escribir la solución
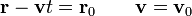
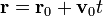
Hemos llegado al resultado conocido de que una partícula libre describe un movimiento rectilíneo y uniforme siguiendo un camino más complicado que el habitual. Sin embargo, en muchos problemas más complicados, el uso de integrales primeras es el método más sencillo e intuitivo.
