Diagrama T-S

De Laplace

(Diferencias entre revisiones)

última version al 19:54 1 jun 2009

Contenido

1 Definición
2 Procesos isotermos
3 Procesos adiabáticos
4 Ciclo de Carnot
5 Caso de un gas ideal
- 5.1 Procesos isóbaros
- 5.2 Procesos isócoros
6 Ciclos termodinámicos

1 Definición

Al definirse la entropía como una función de estado de un sistema, se hace posible describir el estado de dicho sistema, así como los procesos reversibles que en él ocurren, a través de un diagrama en el cual se representa la temperatura del sistema frente a su entropía.

Este es el llamado diagrama T-S en el cual se sitúa la entropía en el eje de abscisas y la temperatura en el de ordenadas. A menudo, en lugar de la entropía, como propiedad extensiva, se emplea la entropía específica (por unidad de masa o por mol) como variable en el eje de abscisas.

Este diagrama es análogo al diagrama PV para un gas ideal, con una diferencia esencial: mientras que un diagrama PV es específico para sistemas mecánicos y no puede aplicarse a otros sistemas termodinámicos, como un paramagnético (para el cual las variables son el campo magnético y la imanación), el diagrama TS posee validez universal, ya que se basa en dos propiedades fundamentales, la temperatura, establecida mediante el Principio Cero de la Termodinámica, y la entropía, definida a partir del Segundo Principio. Por ello, un ciclo de Carnot se representa de la misma forma en un diagrama TS, indpendientemente de que se trate de un gas ideal, un ciclo de agua y vapor, una sustancia paramagnética o cualquier otra.

No obstante, cuando se trata de un proceso específico en un sistema concreto (por ejemplo, un enfriamiento a presión constante en un gas ideal), la curva resultante en el diagrama TS será característica de dicho sistema y no aplicable a otros diferentes.

2 Procesos isotermos

Un proceso isotermo reversible mantiene, por definición, constante la temperatura del sistema. Puesto que en el diagrama TS la temperatura corresponde al eje de ordenadas, un proceso isotermo se representará como una línea y = cte, esto es, como un segmento horizontal.

3 Procesos adiabáticos

Un proceso adiabático es aquél en que el sistema no intercambia calor con el ambiente. Si además el proceso es reversible tenemos que

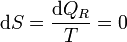
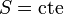
$\mathrm{d}S = \frac{\mathrm{d}Q_R}{T}=0$ $\Rightarrow$ $S=\mathrm{cte}\,$

Es decir, un proceso adiabático reversible es siempre isentrópico. Puesto que la entropía se mide en el eje de abscisas en un diagrama TS, un proceso adiabático reversible corresponde a un segmento vertical. Estará orientado hacia arriba si el sistema se está calentando y hacia abajo si se está enfriando.

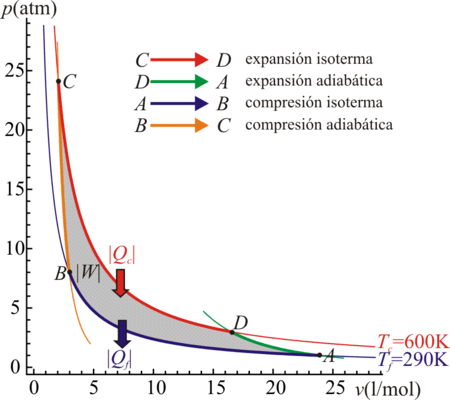
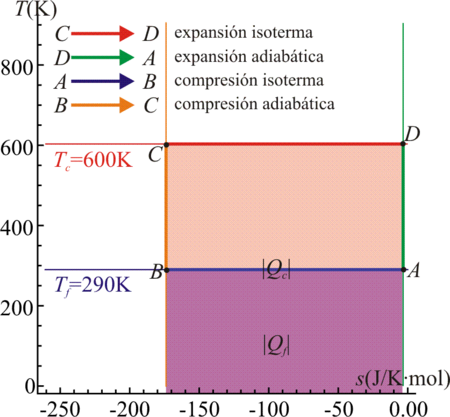
4 Ciclo de Carnot

Los dos procesos anteriores son independientes del sistema al que se apliquen. Por ello, un proceso compuesto de tramos isotermos y tramos adiabáticos se representará de la misma forma sea cual sea el sistema.

En particular, un ciclo de Carnot, formado por dos procesos isotermos y dos adiabáticos, presenta una representación especialmente sencilla.

El ciclo se compone de cuatro pasos:

C→D Absorción de calor $Q c$ en un proceso isotermo a temperatura $T c$ , que corresponde a un segmento horizontal hacia la derecha.

D→A Enfriamiento adiabático hasta la temperatura del foco frío, $T f$ , representable por un segmento vertical hacia abajo.

A→B Cesión de calor $| Q f |$ al foco frío a temperatura $T f$ , que corresponde a un segmento horizontal hacia la izquierda.

B→C Calentamiento adiabático desde la temperatura del foco frío, $T f$ a la temperatura del foco caliente, $T c$ . De nuevo obtenemos un segmento vertical, ahora hacia arriba.

El resultado completo es un rectángulo recorrido en sentido horario.

En este diagrama el calor absorbido $Q c$ es el área del rectángulo delimitado por el lado superior del ciclo y el eje de abscisas, mientras que el calor cedido $| Q f |$ es el área del rectángulo definido por el lado inferior del ciclo y el eje de abscisas. El calor neto, $| Q c | - | Q f |$ , que entra en el sistema es el área del rectángulo delimitado por el ciclo. Por el Primer Principio, este área equivale al trabajo neto efectuado por el sistema, $| W |$ .

Si en vez de una máquina de Carnot tenemos un refrigerador de Carnot, la figura es exactamente la misma, solo que se recorren en sentido opuesto.

5 Caso de un gas ideal

5.1 Procesos isóbaros

En el caso particular de un gas ideal, podemos trazar las curvas correspondientes a procesos a presión y a volumen constante, puesto que disponemos de expresiones explícitas para la entropía de un gas ideal.

En términos de la temperatura y la presión, la entropía de un gas ideal es igual a

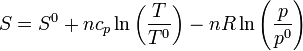
$S = S^0+ n c_p \ln\left(\frac{T}{T^0}\right)-n R \ln\left(\frac{p}{p^0}\right)$

siendo $T 0$ , $p 0$ y $S 0$ la temperatura, presión y entropía de un cierto estado de referencia.

Si en vez de la entropía total consideramos la específica, por mol, la ecuación anterior nos queda

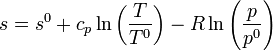
$s = s^0 + c_p \ln\left(\frac{T}{T^0}\right)- R \ln\left(\frac{p}{p^0}\right)$

Despejando de aquí la temperatura

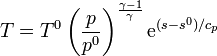
$T = T^0 \left(\frac{p}{p^0}\right)^\frac{\gamma-1}{\gamma}\mathrm{e}^{(s-s^0)/c_p}$

ya que

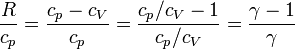
$\frac{R}{c_p} = \frac{c_p-c_V}{c_p}=\frac{c_p/c_V-1}{c_p/c_V}= \frac{\gamma-1}{\gamma}$

La ecuación anterior nos dice que en un diagrama TS un proceso a presión constante se representa por una curva exponencial creciente de la temperatura como función de la entropía.

5.2 Procesos isócoros

De manera análoga podemos representar los procesos a volumen constante. La entropía por mol de un gas ideal es, en función de la temperatura y el volumen molar $v = V / n$

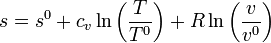
$s = s^0 + c_v \ln\left(\frac{T}{T^0}\right) + R \ln\left(\frac{v}{v^0}\right)$

Despejando la temperatura

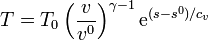
$T = T_0\left(\frac{v}{v^0}\right)^{\gamma-1} \mathrm{e}^{(s-s^0)/c_v}$

Vemos que las curvas isócoras son también exponenciales pero con un factor de crecimiento diferente. Puesto que $c v < c p$ esto quiere decir que las isócoras poseen una pendiente mayor que las isóbaras.

6 Ciclos termodinámicos

Combinando los procesos anteriores pueden trazarse procesos cíclicos en un diagrama TS. En todos los casos, el área encerrada por el ciclo, en valor absoluto, será el calor neto absorbido o cedido por el sistema que, por el Primer Principio de la termodinámica será igual al trabajo realizado por o sobre el sistema.

El caso más sencillo es el del ciclo de Carnot que ya hemos descrito anteriormente:

Ciclo de Carnot
Diagrama PV	Diagrama TS

Para un sistema de gases ideales podemos analizar otros procesos cíclicos de aplicación práctica, como el ciclo Otto (de los motores de explosión) el Diesel (usado en los motores diésel) y el Brayton (empleado en las turbinas de los aviones).

6.1 Ciclo Otto

Artículo completo: Ciclo Otto

Un ciclo Otto ideal se compone de cuatro procesos (más dos que se cancelan mutuamente):

Brarr;C Absorción de calor $Q c$ en un proceso a volumen constante, que se representa mediante una exponencial recorrida hacia la derecha.

C→D Enfriamiento adiabático, al que corresponde un segmento vertical hacia abajo.

D→A Cesión de calor $| Q f |$ al foco frío a volumen constante, al que le corresponde otra exponencial, ésta recorrida hacia la izquierda.

A→B Calentamiento adiabático desde el volumen máximo al mínimo. De nuevo obtenemos un segmento vertical, ahora hacia arriba.

Ciclo Otto
Diagrama PV	Diagrama TS
	Archivo:Ciclo-otto-ts.png

6.2 Ciclo Diesel

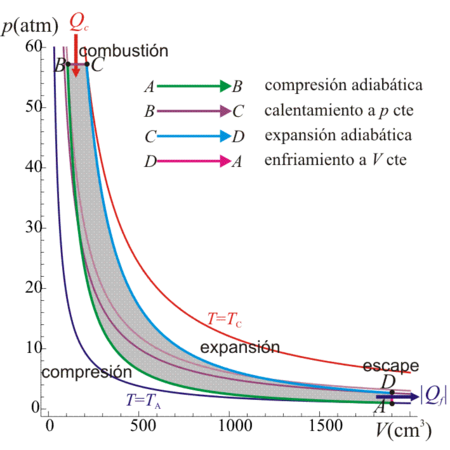
Artículo completo: Ciclo Diesel

Un ciclo Diesel ideal se compone también de cuatro procesos:

Brarr;C Absorción de calor $Q c$ en un proceso a presión constante, que se representa mediante una exponencial recorrida hacia la derecha. Éste es el único paso en que se diferencia del ciclo Otto. Puesto que en ambos casos tenemos exponenciales, es dificil distinguir ambos ciclos en un diagrama TS (mientras que en uno PV es evidente la diferencia).

C→D Enfriamiento adiabático, al que corresponde un segmento vertical hacia abajo.

D→A Cesión de calor $| Q f |$ al foco frío a volumen constante, al que le corresponde otra exponencial, ésta recorrida hacia la izquierda.

A→B Calentamiento adiabático desde el volumen máximo al mínimo. De nuevo obtenemos un segmento vertical, ahora hacia arriba.

Ciclo Diesel
Diagrama PV	Diagrama TS
	Archivo:Ciclo-diesel-ts.png

6.3 Ciclo Brayton

@@ Línea 39: / Línea 39: @@
 Si en vez de una máquina de Carnot tenemos un refrigerador de Carnot, la figura es exactamente la misma, solo que se recorren en sentido opuesto.
-==Procesos isóbaros==
+==Caso de un gas ideal==
-==Procesos isócoros==
+===Procesos isóbaros===
+En el caso particular de un gas ideal, podemos trazar las curvas correspondientes a procesos a presión y a volumen constante, puesto que disponemos de expresiones explícitas para la entropía de un gas ideal.
+En términos de la temperatura y la presión, la entropía de un gas ideal es igual a
+<center><math>S = S^0+ n c_p \ln\left(\frac{T}{T^0}\right)-n R \ln\left(\frac{p}{p^0}\right)</math></center>
+siendo <math>T^0</math>, <math>p^0</math> y <math>S^0</math> la temperatura, presión y entropía de un cierto estado de referencia.
+Si en vez de la entropía total consideramos la específica, por mol, la ecuación anterior nos queda
+<center><math>s = s^0 + c_p \ln\left(\frac{T}{T^0}\right)- R \ln\left(\frac{p}{p^0}\right)</math></center>
+Despejando de aquí la temperatura
+<center><math>T = T^0 \left(\frac{p}{p^0}\right)^\frac{\gamma-1}{\gamma}\mathrm{e}^{(s-s^0)/c_p}</math></center>
+ya que
+<center><math>\frac{R}{c_p} = \frac{c_p-c_V}{c_p}=\frac{c_p/c_V-1}{c_p/c_V}= \frac{\gamma-1}{\gamma}</math></center>
+La ecuación anterior nos dice que en un diagrama TS un proceso a presión constante se representa por una curva exponencial creciente de la temperatura como función de la entropía.
+===Procesos isócoros===
+De manera análoga podemos representar los procesos a volumen constante. La entropía por mol de un gas ideal es, en función de la temperatura y el volumen molar <math>v = V/n</math>
+<center><math>s = s^0 + c_v \ln\left(\frac{T}{T^0}\right) + R \ln\left(\frac{v}{v^0}\right)</math></center>
+Despejando la temperatura
+<center><math>T = T_0\left(\frac{v}{v^0}\right)^{\gamma-1} \mathrm{e}^{(s-s^0)/c_v}</math></center>
+Vemos que las curvas isócoras son también exponenciales pero con un factor de crecimiento diferente. Puesto que <math>c_v < c_p</math> esto quiere decir que las isócoras poseen una pendiente mayor que las isóbaras.
 ==Ciclos termodinámicos==
+Combinando los procesos anteriores pueden trazarse procesos cíclicos en un diagrama TS. En todos los casos, el área encerrada por el ciclo, en valor absoluto, será el calor neto absorbido o cedido por el sistema que, por el Primer Principio de la termodinámica será igual al trabajo realizado por o sobre el sistema.
+El caso más sencillo es el del ciclo de Carnot que ya hemos descrito anteriormente:
+<center>
+{|class="bordeado"
+|+ Ciclo de Carnot
+|-
+| [[Imagen:ciclo-carnot-pv.png|450px]]
+| [[Imagen:Ciclo-carnot-ts.png|450px]]
+|-
+! Diagrama PV
+! Diagrama TS
+|-
+|}
+</center>
+Para un sistema de gases ideales podemos analizar otros procesos cíclicos de aplicación práctica, como el ciclo Otto (de los motores de explosión) el Diesel (usado en los motores diésel) y el Brayton (empleado en las turbinas de los aviones).
 ===Ciclo Otto===
+{{ac|Ciclo Otto}}
+Un ciclo Otto ideal se compone de cuatro procesos (más dos que se cancelan mutuamente):
+* Brarr;C Absorción de calor <math>Q_c</math> en un proceso a volumen constante, que se representa mediante una exponencial recorrida hacia la derecha.
+* C&rarr;D Enfriamiento adiabático, al que corresponde un segmento vertical hacia abajo.
+* D&rarr;A Cesión de calor <math>|Q_f|</math> al foco frío a volumen constante, al que le corresponde otra exponencial, ésta recorrida hacia la izquierda.
+* A&rarr;B Calentamiento adiabático desde el volumen máximo al mínimo. De nuevo obtenemos un segmento vertical, ahora hacia arriba.
+<center>
+{|class="bordeado"
+|+ Ciclo Otto
+|-
+| [[Imagen:ciclo-otto-exacto.png|450px]]
+| [[Imagen:Ciclo-otto-ts.png|450px]]
+|-
+! Diagrama PV
+! Diagrama TS
+|-
+|}
+</center>
 ===Ciclo Diesel===
-===Ciclo de Stirling===
+{{ac|Ciclo Diesel}}
+Un ciclo Diesel ideal se compone también de cuatro procesos:
+* Brarr;C Absorción de calor <math>Q_c</math> en un proceso a presión constante, que se representa mediante una exponencial recorrida hacia la derecha. Éste es el único paso en que se diferencia del ciclo Otto. Puesto que en ambos casos tenemos exponenciales, es dificil distinguir ambos ciclos en un diagrama TS (mientras que en uno PV es evidente la diferencia).
+* C&rarr;D Enfriamiento adiabático, al que corresponde un segmento vertical hacia abajo.
+* D&rarr;A Cesión de calor <math>|Q_f|</math> al foco frío a volumen constante, al que le corresponde otra exponencial, ésta recorrida hacia la izquierda.
+* A&rarr;B Calentamiento adiabático desde el volumen máximo al mínimo. De nuevo obtenemos un segmento vertical, ahora hacia arriba.
+<center>
+{|class="bordeado"
+|+ Ciclo Diesel
+|-
+| [[Imagen:ciclo-diesel-exacto.png|450px]]
+| [[Imagen:Ciclo-diesel-ts.png|450px]]
+|-
+! Diagrama PV
+! Diagrama TS
+|-
+|}
+</center>
+===Ciclo Brayton===
 [[Categoría:Segundo Principio]]

Diagrama T-S

De Laplace

última version al 19:54 1 jun 2009

Contenido

1 Definición

2 Procesos isotermos

3 Procesos adiabáticos

4 Ciclo de Carnot

5 Caso de un gas ideal

5.1 Procesos isóbaros

5.2 Procesos isócoros

6 Ciclos termodinámicos

6.1 Ciclo Otto

6.2 Ciclo Diesel

6.3 Ciclo Brayton

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES