Posición aparente de un avión supersónico
De Laplace
(Nueva página: == Enunciado == Un avión supersónico vuela a Mach 1.8 a 3 km de altura. Determine el tiempo entre que pasa por la vertical de un observador situado en el suelo y que a éste...) |
(→Solución) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 4: | Línea 4: | ||
== Solución == | == Solución == | ||
| + | |||
| + | [[Imagen:Posicion_aparente_avion_supersonico.png|right]] | ||
| + | |||
| + | Un avión que viaja a velocidad supersónica emite una onda de choque en todo instante, no sólo cuando | ||
| + | rompe la barrera del sonido. La onda de choque se propaga con una ángulo <math>\theta</math> respecto | ||
| + | a la dirección de movimiento del avión (las líneas rojas en la figura). Éste es el ángulo de Mach. El | ||
| + | número de Mach se define como | ||
| + | <center> | ||
| + | <math> | ||
| + | M=\frac{1}{\mathrm{sen}\,\theta} | ||
| + | </math> | ||
| + | </center> | ||
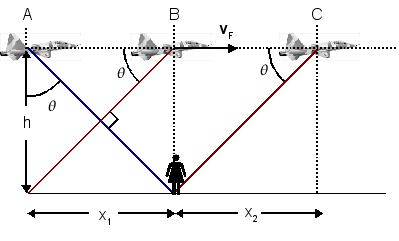
| + | La figura adjunta muestra la posición del avión cuando emitió la onda de choque que percibe el observador | ||
| + | (A), cuando está en la vertical del observador (B) y cuando la | ||
| + | onda de choque llega a la posición del observador (C). La línea azul, que indica el camino seguido por la onda | ||
| + | de choque detectada por el observador, es perpendicular a la onda de choque. En la figura se indica también | ||
| + | las otras apariciones del ángulo <math>\theta</math>. A partir de la definición del número de Mach tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{lcccr} | ||
| + | \displaystyle\mathrm{sen}\,\theta=\frac{1}{M},&& | ||
| + | \displaystyle\cos\theta=\frac{\sqrt{M^2-1}}{M},&& | ||
| + | \displaystyle\tan\theta=\frac{1}{\sqrt{M^2-1}} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Como tenemos el dato de la altura a la que viaja el avión, <math>h=3\,\mathrm{km}</math>, y el número de Mach, | ||
| + | <math>M=1.8</math>, podemos determinar las distancias <math>x_1</math> y <math>x_2</math> en el dibujo. | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{l} | ||
| + | \displaystyle x_1 = h\,\tan\theta=\frac{h}{\sqrt{M^2-1}}=2.00\,\mathrm{km}\\ \\ | ||
| + | \displaystyle x_2 = \frac{h}{\tan\theta}=h\sqrt{M^2-1}=4.49\,\mathrm{km} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Entre el instante en el que el el avión pasa por la vertical del observador y éste recibe la onda de choque | ||
| + | emitida por el avión en el punto A, el avión ha recorrido la distancia <math>x_2</math>. La velocidad del avión es | ||
| + | <center> | ||
| + | <math> | ||
| + | v_F=M\,c=617\,\mathrm{m/s}=2.22\times10^3\,\mathrm{km/h} | ||
| + | </math> | ||
| + | </center> | ||
| + | Por tanto, el tiempo que tarda el avión en recorrer la distancia <math>x_2</math> es | ||
| + | <center> | ||
| + | <math> | ||
| + | t_2=\frac{x_2}{v_f}=\frac{x_2}{M\,c}=\frac{h\sqrt{M^2-1}}{c\,M}=7.28\,\mathrm{s} | ||
| + | </math> | ||
| + | </center> | ||
| + | Cuando el observador recibe la onda de choque el avión está en el punto C. Por tanto, la distancia entre el observador | ||
| + | y el avión es | ||
| + | <center> | ||
| + | <math> | ||
| + | d=\frac{h}{\mathrm{sen}\theta}=M\,h=5.4\,\mathrm{km} | ||
| + | </math> | ||
| + | </center> | ||
| + | [[Categoría:Problemas de ondas sonoras]] | ||
última version al 20:40 2 may 2009
1 Enunciado
Un avión supersónico vuela a Mach 1.8 a 3 km de altura. Determine el tiempo entre que pasa por la vertical de un observador situado en el suelo y que a éste le llegue el frente de la onda de choque. Cuando llega este sonido, ¿dónde parece que se encuentra el avión, a juzgar por el ruido? ¿A qué distancia de su posición real en ese instante?
2 Solución
Un avión que viaja a velocidad supersónica emite una onda de choque en todo instante, no sólo cuando rompe la barrera del sonido. La onda de choque se propaga con una ángulo θ respecto a la dirección de movimiento del avión (las líneas rojas en la figura). Éste es el ángulo de Mach. El número de Mach se define como
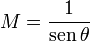
La figura adjunta muestra la posición del avión cuando emitió la onda de choque que percibe el observador (A), cuando está en la vertical del observador (B) y cuando la onda de choque llega a la posición del observador (C). La línea azul, que indica el camino seguido por la onda de choque detectada por el observador, es perpendicular a la onda de choque. En la figura se indica también las otras apariciones del ángulo θ. A partir de la definición del número de Mach tenemos
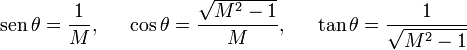
Como tenemos el dato de la altura a la que viaja el avión, 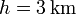 , y el número de Mach,
M = 1.8, podemos determinar las distancias x1 y x2 en el dibujo.
, y el número de Mach,
M = 1.8, podemos determinar las distancias x1 y x2 en el dibujo.
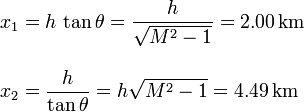
Entre el instante en el que el el avión pasa por la vertical del observador y éste recibe la onda de choque emitida por el avión en el punto A, el avión ha recorrido la distancia x2. La velocidad del avión es
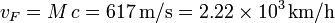
Por tanto, el tiempo que tarda el avión en recorrer la distancia x2 es
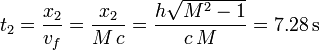
Cuando el observador recibe la onda de choque el avión está en el punto C. Por tanto, la distancia entre el observador y el avión es