Diamagnético
De Laplace
(→Comportamiento de un diamagnético. Levitación) |
(→Comportamiento de un diamagnético. Levitación) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 64: | Línea 64: | ||
<center><math>\mathbf{m}=\alpha\mathbf{B}</math></center> | <center><math>\mathbf{m}=\alpha\mathbf{B}</math></center> | ||
| - | con <math>\alpha</math> una constante de proporcionalidad, negativa en este caso (en el caso particular de una [[Partícula_magnética_en_un_campo_externo#Magnetizaci.C3.B3n_y_campo|partícula esférica]] su valor es <math>\alpha=3 | + | con <math>\alpha</math> una constante de proporcionalidad, negativa en este caso (en el caso particular de una [[Partícula_magnética_en_un_campo_externo#Magnetizaci.C3.B3n_y_campo|partícula esférica]] su valor es <math>\alpha=3\chi_m\tau/\mu_0(3+\chi_m)</math>). La [[Acción_de_un_campo_magnético_sobre_un_dipolo_magnético#Fuerza|fuerza]] sobre esta partícula será |
<center><math>\mathbf{F}=(\mathbf{m}\times\nabla)\times\mathbf{B})=\alpha(\mathbf{B}\times\nabla)\times\mathbf{B})</math></center> | <center><math>\mathbf{F}=(\mathbf{m}\times\nabla)\times\mathbf{B})=\alpha(\mathbf{B}\times\nabla)\times\mathbf{B})</math></center> | ||
| Línea 72: | Línea 72: | ||
<center><math>\mathbf{F}=-\nabla U</math>{{qquad}}{{qquad}}<math>U=-\frac{\alpha}{2}|\mathbf{B}|^2</math></center> | <center><math>\mathbf{F}=-\nabla U</math>{{qquad}}{{qquad}}<math>U=-\frac{\alpha}{2}|\mathbf{B}|^2</math></center> | ||
| - | (Obsérvese que en este caso, la energía potencial no coincide con [[Acción_de_un_campo_magnético_sobre_un_dipolo_magnético#Energ.C3.ADa| | + | (Obsérvese que en este caso, la energía potencial no coincide con la [[Acción_de_un_campo_magnético_sobre_un_dipolo_magnético#Energ.C3.ADa|energía de un dipolo fijo en un campo externo]]). La fuerza impulsa al dipolo en la dirección de la mínima energía potencial. Teniendo en cuenta que <math>\alpha</math> es negativo, esta energía se puede escribir |
<center><math>U=\frac{|\alpha|}{2}|\mathbf{B}|^2</math></center> | <center><math>U=\frac{|\alpha|}{2}|\mathbf{B}|^2</math></center> | ||
última version al 19:20 22 abr 2009
Contenido |
1 Definición
Poseen una susceptibilidad negativa. En estos materiales, el campo se ve reducido por efecto de la magnetización inducida, que se opone al campo externo. Para casi todos los diamagnéticos 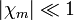 y puede aproximarse
y puede aproximarse 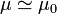 .
.
2 Valores típicos
Algunos ejemplos son
| Material | 105χm | Material | 105χm |
|---|---|---|---|
| Bismuto | -16.6 | Mercurio | -2.9 |
| Plata | -2.6 | Carbono (diamante) | -2.1 |
| Carbono (grafito) | -1.6 | Plomo | -1.8 |
| Cloruro sódico | -1.4 | Cobre | -1.0 |
| Agua | -0.91 | CO2 | -0.0012 |
3 Origen del diamagnetismo
Aunque una explicación correcta del diamagnetismo requiere el uso de mecánica cuántica, puede darse una interpretación cualitativa empleando electromagnetismo clásico.
Según el modelo atómico de Bohr, podemos imaginarnos cada electrón atómico como una pequeña espira de corriente, que llevará asociada un pequeño momento dipolar magnético. En ausencia de campo magnético, la contribución de los electrones que giran en un sentido se cancela con la de los que giran en sentido opuesto y la magnetización será nula.
Si se aplica un campo magnético externo, la variación del flujo a través de cada espira induce un cambio en la corriente, según la ley de Faraday. De acuerdo con la ley de Lenz, la corriente inducida será tal que se opone a la variación del flujo magnético. Puesto que éste ha aumentado, la corriente inducida produce un campo magnético en sentido opuesto. Esto es, el momento magnético debido a la corriente inducida va en sentido opuesto al campo aplicado. Esto es cierto tanto si los electrones giran en un sentido como si giran en el contrario. El resultado es que todos los átomos contribuyen con un dipolo opuesto al campo aplicado, y resulta una magnetización antiparalela al campo. El material se comportará como un diamagnético.
Si este principio es general, cabe entonces preguntarse por qué todos los materiales no se comportan como diamagnéticos. La razón es que el efecto descrito es muy pequeño. Si, superpuestos a él, existe paramagnetismo o ferromagnetismo, la contribución diamagnética es despreciable.
4 Comportamiento de un diamagnético. Levitación
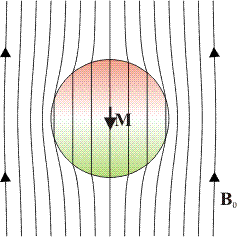
Cuando se coloca una partícula diamagnética en el seno de un campo magnético aparece una magnetización en sentido opuesto al campo magnético . Puesto que la susceptibilidad de un diamagnético es negativa, pero nunca supera el valor -1 (esto es, la permeabilidad siempre es positiva), la imanación también va en sentido opuesto al campo magnético
. Puesto que la susceptibilidad de un diamagnético es negativa, pero nunca supera el valor -1 (esto es, la permeabilidad siempre es positiva), la imanación también va en sentido opuesto al campo magnético  :
:
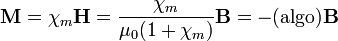
El campo magnético en el interior de un diamagnético será menor que el que campo aplicado: los diamagnéticos reducen el campo magnético.
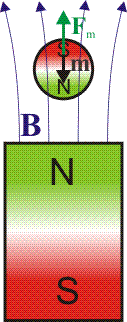
El que la magnetización vaya en sentido opuesto al campo aplicado hace que los materiales diamagnéticos sean repelidos por los imanes. Supongamos una partícula diamagnética situada encima del polo norte de un imán (o de una bobina). El campo aplicado va hacia arriba, por lo que el momento dipolar
aplicado va hacia arriba, por lo que el momento dipolar 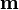 de la partícula va hacia abajo. Al enfrentarse los polos norte, la partícula se ve repelida. Lo mismo si es un polo sur.
de la partícula va hacia abajo. Al enfrentarse los polos norte, la partícula se ve repelida. Lo mismo si es un polo sur.
Aplicando campos muy intensos puede hacerse levitar objetos formados por agua, como una pequeña rana.
Mátematicamente, el dipolo magnético inducido en la partícula será de la forma
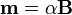
con α una constante de proporcionalidad, negativa en este caso (en el caso particular de una partícula esférica su valor es α = 3χmτ / μ0(3 + χm)). La fuerza sobre esta partícula será
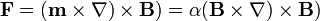
Con ayuda del cálculo vectorial esta fuerza se puede escribir
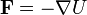
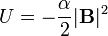
(Obsérvese que en este caso, la energía potencial no coincide con la energía de un dipolo fijo en un campo externo). La fuerza impulsa al dipolo en la dirección de la mínima energía potencial. Teniendo en cuenta que α es negativo, esta energía se puede escribir
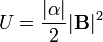
que nos dice que la energía será mínima cuando lo sea el módulo del campo magnético. En términos físicos, una partícula diamagnética tiende a moverse hacia donde el campo es más débil.
Puesto que la interacción entre imanes cumple la 3ª ley de Newton, del mismo modo que podemos decir que una partícula diamagnética tiende a levitar cuando se coloca sobre un imán, también podemos afirmar el recíproco: un imán tiende a levitar cuando se coloca sobre una superficie diamagnética. Este es el fundamento de la levitación en superconductores.