Trabajo en distintos procesos
De Laplace
(Nueva página: == Enunciado == Un mol de un gas ideal está contenido en un cilindro que tiene un émbolo móvil. La presión, volumen y temperatura iniciales son <math>P_i, V_i, T_i</math>, respe...) |
(→Proceso isotermo) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | __TOC__ | ||
== Enunciado == | == Enunciado == | ||
Un mol de un gas ideal está contenido en un cilindro que tiene un émbolo móvil. | Un mol de un gas ideal está contenido en un cilindro que tiene un émbolo móvil. | ||
La presión, volumen y temperatura iniciales son <math>P_i, V_i, T_i</math>, | La presión, volumen y temperatura iniciales son <math>P_i, V_i, T_i</math>, | ||
| - | respectivamente. | + | respectivamente. Calcula el trabajo realizado sobre el gas para los siguientes |
| - | procesos, y | + | procesos, y dibuja cada uno de ellos en un diagrama <math>PV</math> |
#Una compresión isobárica en la que el volumen final sea la mitad del volumen inicial | #Una compresión isobárica en la que el volumen final sea la mitad del volumen inicial | ||
| Línea 9: | Línea 10: | ||
#Un proceso isócoro en el que la presión final sea el triple de la inicial. | #Un proceso isócoro en el que la presión final sea el triple de la inicial. | ||
| - | == | + | ==Introducción == |
| + | |||
| + | En general, el trabajo realizado sobre un sistema hidrostático en un proceso | ||
| + | cuasiestático entre los estados 1 y 2 es | ||
| + | <center> | ||
| + | <math> | ||
| + | W_{12}=-\int\limits_1^2P\mathrm{d} V | ||
| + | </math> | ||
| + | </center> | ||
| + | Para poder calcular esta integral hay que saber como varía la presión en | ||
| + | función del volumen. Examinemos cada uno de los procesos propuestos en el | ||
| + | enunciado | ||
| + | == Proceso isobárico == | ||
| + | En este caso la presión se mantiene constante e igual a la inicial. Los estados | ||
| + | inicial y final son | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{c|c} | ||
| + | \begin{array}{c} | ||
| + | \mathrm{Estado\,1}\\P_1=P_i\\V_1=V_i\\T_1=T_i | ||
| + | \end{array}& | ||
| + | \begin{array}{c} | ||
| + | \mathrm{Estado\,2}\\P_2=P_i\\V_2=V_i/2\\T_2=? | ||
| + | \end{array} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | Como el proceso es a presión constante, ésta puede sacarse de la integral. | ||
| + | Tenemos entonces | ||
| + | <center> | ||
| + | <math> | ||
| + | W_{12}=-\int\limits_1^2P_i\mathrm{d}V=-P_i\int\limits_1^2\mathrm{d}V= | ||
| + | -P_i(V_2-V_1)=P_iV_i/2 | ||
| + | </math> | ||
| + | </center> | ||
| + | El trabajo es positivo, es decir, contribuye a aumentar la energía interna | ||
| + | del gas. Esto es siempre así en una compresión. | ||
| + | |||
| + | == Proceso isotermo == | ||
| + | En este caso la presión varía al realizar el proceso, pero la ecuación | ||
| + | de estado del gas ideal nos da la relación entre presión y volumen. Tenemos | ||
| + | <center> | ||
| + | <math> | ||
| + | PV=nRT\Rightarrow P=\frac{nRT}{V} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | Los estados inicial y final son | ||
| + | <center> | ||
| + | <math> | ||
| + | \begin{array}{c|c} | ||
| + | \begin{array}{c} | ||
| + | \mathrm{Estado\,1}\\P_1=P_i\\V_1=V_i\\T_1=T_i | ||
| + | \end{array}& | ||
| + | \begin{array}{c} | ||
| + | \mathrm{Estado\,2}\\P_2=4P_i\\V_2=?\\T_2=T_i | ||
| + | \end{array} | ||
| + | \end{array} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | EL trabajo es | ||
| + | <center> | ||
| + | <math> | ||
| + | W_{12}=-\int\limits_1^2P\mathrm{d}V=-\int\limits_1^2nRT_i\frac{\mathrm{d}V}{V}= | ||
| + | -nRT_i\int\limits_1^2\frac{\mathrm{d}V}{V}= | ||
| + | -nRT_i\ln\frac{V_2}{V_1} | ||
| + | </math> | ||
| + | </center> | ||
| + | Hemos usado que la temperatura es constante y por tanto puede salir de la | ||
| + | integral. No tenemos el volumen inicial, pero podemos expresar el trabajo | ||
| + | en función de las presiones usando la ley de Boyle. Como el proceso es | ||
| + | isotermo se cumple | ||
| + | <center> | ||
| + | <math> | ||
| + | P_1V_1=P_2V_2\Rightarrow \frac{V_2}{V_1}=\frac{P_1}{P_2} | ||
| + | </math> | ||
| + | </center> | ||
| + | y el trabajo se puede expresar como | ||
| + | <center> | ||
| + | <math> | ||
| + | W_{12}=-nRT_i\ln\frac{P_1}{P_2}=nRT_i\ln\frac{P_2}{P_1} | ||
| + | </math> | ||
| + | </center> | ||
| + | Para comparar con el resultado anterior usamos la ecuación de estado para | ||
| + | expresar la temperatura en función de la presión y volumen iniciales | ||
| + | <center> | ||
| + | <math> | ||
| + | W_{12}=P_iV_i\ln\frac{4P_i}{P_i}=2\ln2P_iV_i | ||
| + | </math> | ||
| + | </center> | ||
| + | De nuevo el trabajo es positivo y puede observarse que es mayor que el | ||
| + | obtenido en el proceso isobárico. | ||
| + | |||
| + | ==Proceso isócoro== | ||
| + | En este caso, al no haber cambio de volumen, no hay trabajo realizado sobre | ||
| + | el gas. Tenemos entonces | ||
| + | <center> | ||
| + | <math> | ||
| + | W_{12}=0 | ||
| + | </math> | ||
| + | </center> | ||
| + | [[Categoría:Problemas del gas ideal]] | ||
última version al 18:00 11 may 2010
Contenido |
1 Enunciado
Un mol de un gas ideal está contenido en un cilindro que tiene un émbolo móvil. La presión, volumen y temperatura iniciales son Pi,Vi,Ti, respectivamente. Calcula el trabajo realizado sobre el gas para los siguientes procesos, y dibuja cada uno de ellos en un diagrama PV
- Una compresión isobárica en la que el volumen final sea la mitad del volumen inicial
- Una compresión isotérmica en la que la presión final se cuatro veces la inicial
- Un proceso isócoro en el que la presión final sea el triple de la inicial.
2 Introducción
En general, el trabajo realizado sobre un sistema hidrostático en un proceso cuasiestático entre los estados 1 y 2 es
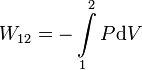
Para poder calcular esta integral hay que saber como varía la presión en función del volumen. Examinemos cada uno de los procesos propuestos en el enunciado
3 Proceso isobárico
En este caso la presión se mantiene constante e igual a la inicial. Los estados inicial y final son
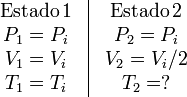
Como el proceso es a presión constante, ésta puede sacarse de la integral. Tenemos entonces
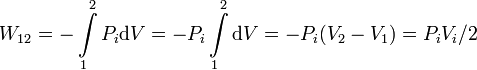
El trabajo es positivo, es decir, contribuye a aumentar la energía interna del gas. Esto es siempre así en una compresión.
4 Proceso isotermo
En este caso la presión varía al realizar el proceso, pero la ecuación de estado del gas ideal nos da la relación entre presión y volumen. Tenemos
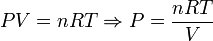
Los estados inicial y final son
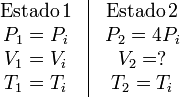
EL trabajo es
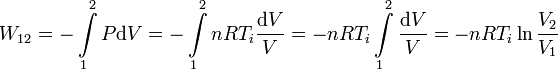
Hemos usado que la temperatura es constante y por tanto puede salir de la integral. No tenemos el volumen inicial, pero podemos expresar el trabajo en función de las presiones usando la ley de Boyle. Como el proceso es isotermo se cumple
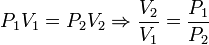
y el trabajo se puede expresar como
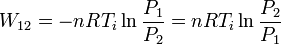
Para comparar con el resultado anterior usamos la ecuación de estado para expresar la temperatura en función de la presión y volumen iniciales
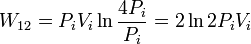
De nuevo el trabajo es positivo y puede observarse que es mayor que el obtenido en el proceso isobárico.
5 Proceso isócoro
En este caso, al no haber cambio de volumen, no hay trabajo realizado sobre el gas. Tenemos entonces
W12 = 0





