Dipolo magnético
De Laplace
(→Ejemplo: Una esfera rotante) |
(→Dipolos de Ampère y dipolos de Gilbert) |
||
| (28 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | == | + | ==Definición== |
| - | + | Un dipolo magnético es un elemento puntual que produce un campo magnético dipolar | |
| - | + | <center><math>\mathbf{B}=\frac{\mu_0}{4\pi}\,\frac{3(\mathbf{m}\cdot\mathbf{r})\mathbf{r}-r^2\mathbf{m}}{r^5}</math></center> | |
| - | + | (situando el origen de coordenadas en el elemento). Este campo corresponde a un potencial vector | |
| - | + | <center><math>\mathbf{A}=\frac{\mu_0}{4\pi}\,\frac{\mathbf{m}\times\mathbf{r}}{r^3}</math></center> | |
| - | + | Aunque lo habitual es definir el dipolo magnético como una pequeña espira o distribución de corriente, realmente lo que lo define es el campo que produce. Una partícula elemental, como el electrón, produce un campo magnético dipolar y por tanto es un dipolo magnético aunque no sea una corriente eléctrica. | |
| - | + | ==Distribución del campo magnético== | |
| + | El campo magnético de un dipolo magnético posee la misma estructura que el campo eléctrico de un dipolo eléctrico: líneas en forma de lóbulos que van del polo norte del dipolo hacia el polo sur. | ||
| - | + | En coordenadas esféricas, el potencial vector de un dipolo se escribe | |
| - | + | <center><math>\mathbf{A}=\frac{\mu_0m\,\mathrm{sen}\,\theta}{4\pi r^2}\mathbf{u}_\varphi</math></center> | |
| - | + | (tomando la dirección del eje Z como a la que apunta el dipolo). El campo correspondiente es | |
| - | + | <center><math>\mathbf{B}=\frac{\mu_0m}{4\pi r^3}(2\cos\theta\mathbf{u}_r+\,\mathrm{sen}\,\theta\mathbf{u}_\theta)</math></center> | |
| - | + | El campo magnético depende de la distancia como <math>1/r^3</math>, esto es, a doble de distancia, octava parte de campo. | |
| - | es | + | ==Momento dipolar magnético== |
| + | La cantidad que caracteriza a un dipolo es su ''momento magnético dipolar'', <math>\mathbf{m}</math>. | ||
| - | + | De las expresiones anteriores, se deduce que la unidad del momento magnético en el Sistema Internacional es 1 A·m² (o, equivalentemente 1 J/T). Este valor es muy grande para las situaciones habituales. Por ejemplo, los momentos de las partículas elementales son cantidades del orden de un [http://es.wikipedia.org/wiki/Magnetón_de_Bohr magnetón de Bohr] | |
| - | + | <center><math>\mu_\mathrm{B} = {{e \hbar} \over {2 m_\mathrm{e}c}}= 927.400 915(23)\times 10^{-26}\frac{\mathrm{A}}{\mathrm{m}^2}</math></center> | |
| - | + | Este momento dipolar puede provenir de la existencia de una corriente localizada, o ser una propiedad intrínseca del sistema, asociada al espín. | |
| - | + | ===Para una distribución de corriente=== | |
| + | {{ac|Desarrollo multipolar magnético}} | ||
| + | Al desarrollar el potencial vector magnético de una distribución localizada de corriente se obtiene que el primer término no nulo del desarrollo es el término dipolar. El valor de <math>\mathbf{m}</math> para una pequeña espira de corriente es | ||
| - | + | <center><math>\mathbf{m}=I\mathbf{S}=\frac{I}{2}\oint_\Gamma\mathbf{r}\times\mathrm{d}\mathbf{r}</math></center> | |
| - | + | siendo <math>\mathbf{S}</math> el [[vector superficie]] correspondiente a la curva. | |
| - | + | Las expresiones correspondientes a una distribución volumétrica y una superficial son | |
| - | == | + | <center><math>\mathbf{m}= \frac{1}{2}\int \mathbf{r}'\times\mathbf{J}\,\mathrm{d}\tau'</math>{{qquad}}{{qquad}}<math>\mathbf{m}= \frac{1}{2}\int \mathbf{r}'\times\mathbf{K}\,\mathrm{d}S'</math></center> |
| - | + | ||
| - | + | En caso de que tengamos varias distribuciones simultáneamente, el momento dipolar será la superposición de los momentos individuales. | |
| - | + | ====Ejemplo: espira==== | |
| + | * Para una espira plana, el momento magnético tiene por módulo el producto de la corriente por el área de la porción plana delimitado por la espira, y por sentido el normal a la superficie, según la regla de la mano derecha (si la corriente es positiva; en sentido opuesto en caso contrario). | ||
| - | + | <center>[[Imagen:momentom1.png]]</center> | |
| - | + | Como ejemplos elementales: | |
| - | + | ; Espira rectangular: En el caso más sencillo, de una espira rectangular de lados <math>a</math> y <math>b</math>, el momento magnético será | |
| - | <center><math> | + | <center><math>\mathbf{m}=Iab\mathbf{n}\,</math></center> |
| - | + | :Si consideramos los lados de la espira como vectores, esta expresión equivale a | |
| - | <center><math> | + | <center><math>\mathbf{m}=I\mathbf{a}\times\mathbf{b}\,</math></center> |
| - | + | ;Espira circular: Para una espira circular el momento es | |
| - | <center><math> | + | <center><math>\mathbf{m}=I\pi R^2\,\mathbf{n}</math></center> |
| - | + | ||
| - | El | + | * Para una espira alabeada el vector superficie tiene por componentes las áreas de las proyecciones de la superficie sobre los planos coordenados. El momento magnético es igual a este vector multiplicado por la corriente. |
| - | <center> | + | <center>[[Imagen:vectorsuperficie.png]]</center> |
| - | + | ; Espira tridimensional: Consideremos una espira alabeada formada por tres cuadrantes de circunferencia, de radio <math>R</math> que van de <math>R\mathbf{u}_x</math> a <math>R\mathbf{u}_y</math>, de ahí a <math>R\mathbf{u}_z</math>, y de vuelta a <math>R\mathbf{u}_x</math>. Tal como se ve en artículo sobre el [[vector superficie]], para esta superficie tenemos | |
| - | <center><math>\mathbf{ | + | <center><math>\mathbf{m}=I\mathbf{S}=\frac{I\pi R^2}{4}(\mathbf{u}_x+\mathbf{u}_y+\mathbf{u}_z)</math></center> |
| - | + | ====Ejemplo: esfera rotante==== | |
| + | {{ac|Momento magnético de una esfera en rotación}} | ||
| + | Un caso particular de corriente de volumen localizada en el espacio es el de una distribución de carga en rotación. Este modelo puede ayudar a describir el comportamiento de una partícula cargada, como un electrón, que se caracteriza por un momento angular (el espín), equivalente en ciertos aspectos a una rotación. | ||
| - | < | + | Supongamos una esfera de radio <math>R</math>, con una carga <math>q</math> distribuida uniformemente en el volumeny que gira en torno a un eje (que tomaremos como eje Z) con velocidad angular <math>\mathbf{w}</math>. Para este sistema la densidad de corriente es, en esféricas |
| - | + | <center><math>\mathbf{J}=\rho_0\mathbf{v}=\rho_0\mathbf{w}\times\mathbf{r}=\rho_0\omega r\,\mathrm{sen}\,\theta\,\mathbf{u}_\varphi</math>{{qquad}}{{qquad}}<math>\rho_0=\frac{q}{4\pi R^3/3}</math></center> | |
| - | + | llevando esto a la integral resulta el momento magnético | |
| - | <center><math> | + | <center><math>\mathbf{m}=\frac{q R^2}{5}\mathbf{w}</math></center> |
| - | que | + | Lo más destacado de este resultado es que es proporcional a la velocidad angular de la partícula. Puesto que lo mismo ocurre con el momento angular |
| - | <center><math> | + | <center><math>\mathbf{L}=\frac{2}{5}mR^2\mathbf{w}</math></center> |
| - | + | puede establecerse una relación de proporcionalidad entre el momento magnético y el momento angular | |
| - | <center><math> | + | <center><math>\mathbf{m}=\frac{q}{2m}\mathbf{L}=\gamma\mathbf{L}</math></center> |
| - | + | A la cantidad <math>\gamma</math> se la denomina razón giromagnética de la partícula. | |
| - | + | ===Momentos intrínsecos=== | |
| + | Además de los momentos asociados a corrientes, cada partícula elemental posee un momento dipolar intrínseco, proporcional a su espín, según la ley | ||
| - | + | <center><math>\mathbf{m}=g\frac{q}{2m}\mathbf{S}</math></center> | |
| - | + | Esta ley es exactamente la misma que la que se cumple para una esfera en rotación. La única diferencia es la aparición de una constante de proporcionalidad adicional llamada [http://en.wikipedia.org/wiki/G-factor factor-g] (que para un [http://physics.nist.gov/cgi-bin/cuu/Value?gem electrón] vale aproximadamente 2). Esto hace que, aunque un electrón no es una esfera rotante, se pueda hablar de su momento magnético como debido a su giro. | |
| - | + | ==Acción de un campo externo sobre un dipolo== | |
| + | {{ac|Acción de un campo magnético sobre un dipolo magnético}} | ||
| + | Las expresiones anteriores hablan del campo magnético causado por un dipolo magnético, pero no del efecto que un campo magnético externo produce sobre este dipolo. | ||
| - | + | Este efecto es análogo al caso de un dipolo eléctrico en el seno de un campo eléctrico. El dipolo experimenta una fuerza y un momento de una fuerza, y posee una cierta energía potencial | |
| + | ===Fuerza=== | ||
| + | La fuerza experimentada por un dipolo magnético en un campo externo es | ||
| - | + | <center><math>\mathbf{F}= \nabla(\mathbf{m}{\cdot}\mathbf{B}_\mathrm{ext})</math></center> | |
| - | + | ===Par y momento=== | |
| + | El momento sobre el dipolo se compone del momento de la fuerza aplicada, más un término intrínseco: | ||
| - | = | + | <center><math>\mathbf{M}=\mathbf{r}\times\mathbf{F} + \mathbf{m}\times\mathbf{B}_\mathrm{ext}</math></center> |
| - | + | ||
| - | + | ||
| - | + | El segundo término representa un par intrínseco. Cuando hay fuerzas de rozamiento, de forma que el dipolo termina por quedarse quieto, el resultado es que el dipolo se alinea con el campo magnético, lo que constituye el fundamento de las brújulas. | |
| - | + | ===Energía=== | |
| + | Tanto la fuerza como el momento pueden derivarse de la energía de un dipolo en un campo externo | ||
| - | + | <center><math>U_\mathrm{m}=-\mathbf{m}{\cdot}\mathbf{B}_\mathrm{ext}</math></center> | |
| - | + | Esta energía es mínima cuando el dipolo apunta en la misma dirección y sentido que el campo aplicado sobre él. | |
| - | + | ==Dipolos de Ampère y dipolos de Gilbert== | |
| + | Comparando la expresión del campo magnético con la con el campo eléctrico debido a | ||
| + | un dipolo eléctrico | ||
| - | <center> | + | <center><math>\mathbf{B}=\frac{\mu_0}{4\pi}\frac{3(\mathbf{m}\cdot\mathbf{r})\mathbf{r}-r^2\mathbf{m}}{r^5}</math>{{qquad}}{{qquad}}<math>\mathbf{E}=\frac{1}{4\pi\varepsilon_0}\frac{3(\mathbf{p}\cdot\mathbf{r})\mathbf{r}-r^2\mathbf{p}}{r^5}</math></center> |
| - | + | vemos que son formalmente idénticos. Según esto, una corriente eléctrica localizada produce en puntos alejados de ella un campo magnético idéntico al que producirían dos cargas (magnéticas, en este caso) muy próximas entre sí. | |
| - | + | ||
| - | + | Esto permite dos visiones de los dipolos magnéticos (que sólo son percibidos por el campo que producen). Una, debida a Ampère, considera que todos los dipolos magnéticos son pequeñas espiras de corriente. La otra, concebida por Gilbert, supone la existencia de polos magnéticos separados dentro de cada dipolo. | |
| - | : | + | <center> |
| + | {| class="bordeado" | ||
| + | |- | ||
| + | | [[Imagen:dipolo-ampere.png]] | ||
| + | | [[Imagen:dipolo-gilbert.png]] | ||
| + | |- | ||
| + | | Modelo de dipolo de Ampère | ||
| + | | Modelo de dipolo de Gilbert | ||
| + | |} | ||
| + | </center> | ||
| - | + | En el modelo de Gilbert, cada dipolo estaría formado por un polo norte (manantial de campo magnético) y un polo sur (sumidero). En el modelo de Ampère la espira define una cara norte (de la que salen las líneas de campo magnético) y una cara sur (por la que entran), obedeciendo la regla de la mano derecha. | |
| - | + | Desde el punto de vista del campo que producen, ambos modelos son casi indistinguibles (sólo se diferencian en su valor justo en el punto donde se encuentra el dipolo, que no suele ser accesible.). Es un hecho, además, que existen momentos dipolares, como el debido al | |
| + | espín -en particular, el del neutrón- que no están producidos por espiras de corriente. El problema es saber si estos momentos dipolares se comportan como los del tipo de Ampère o los de Gilbert. La principal diferencia estriba en la relación con el momento angular. Un dipolo de Ampère debe llevar aparejado siempre un momento angular, mientras que un dipolo de Gilbert no tiene por qué. La experiencia muestra que todos los dipolos, microscópicos o macroscópicos, corresponden a dipolos de Ampère y pueden ser tratados como espiras de corriente. | ||
| - | + | Esta asociación con el momento angular se pone de manifiesto al considerar el efecto de un campo magnético externo sobre un dipolo. El momento de las fuerzas sobre un dipolo magnético en un campo uniforme es | |
| - | + | <center><math>\mathbf{M}= \mathbf{m}\times\mathbf{B}\,</math></center> | |
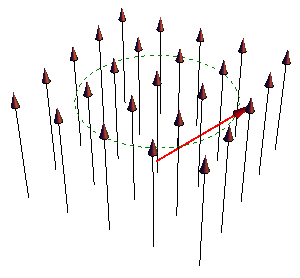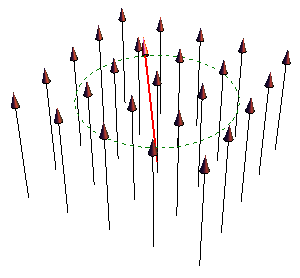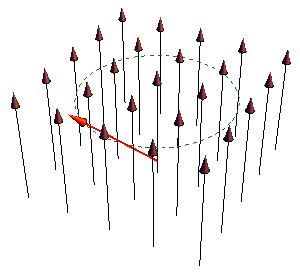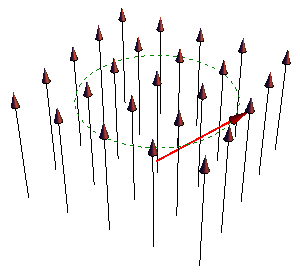
| - | + | [[Imagen:precesion.gif|right]] Conocido el momento, la variación del momento angular es | |
| - | = | + | <center><math>\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}=\mathbf{m}\times\mathbf{B}</math></center> |
| - | + | ||
| - | + | y, de acuerdo con la proporcionalidad entre el momento magnético y el momento angular resulta | |
| - | = | + | <center><math>\frac{\mathrm{d}\mathbf{m}}{\mathrm{d}t}=\gamma\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t} = \gamma \mathbf{m}\times\mathbf{B}</math></center> |
| - | {{ | + | |
| - | + | ||
| - | + | ecuación que predice que un dipolo magnético, en ausencia de fuerzas disipativas, no se orienta en la dirección del campo externo (como hace un dipolo eléctrico, o como haría un dipolo de Gilbert), sino que ''precesa'' en torno a el. Es éste fenómeno el que permite identificar a los momentos dipolares de las partículas como amperianos. | |
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
[[Categoría:Campo magnético de corrientes estacionarias]] | [[Categoría:Campo magnético de corrientes estacionarias]] | ||
| + | [[Categoría:Materiales magnéticos]] | ||
última version al 11:59 29 abr 2009
Contenido |
1 Definición
Un dipolo magnético es un elemento puntual que produce un campo magnético dipolar
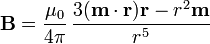
(situando el origen de coordenadas en el elemento). Este campo corresponde a un potencial vector
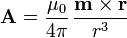
Aunque lo habitual es definir el dipolo magnético como una pequeña espira o distribución de corriente, realmente lo que lo define es el campo que produce. Una partícula elemental, como el electrón, produce un campo magnético dipolar y por tanto es un dipolo magnético aunque no sea una corriente eléctrica.
2 Distribución del campo magnético
El campo magnético de un dipolo magnético posee la misma estructura que el campo eléctrico de un dipolo eléctrico: líneas en forma de lóbulos que van del polo norte del dipolo hacia el polo sur.
En coordenadas esféricas, el potencial vector de un dipolo se escribe
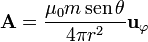
(tomando la dirección del eje Z como a la que apunta el dipolo). El campo correspondiente es
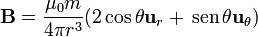
El campo magnético depende de la distancia como 1 / r3, esto es, a doble de distancia, octava parte de campo.
3 Momento dipolar magnético
La cantidad que caracteriza a un dipolo es su momento magnético dipolar, 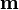 .
.
De las expresiones anteriores, se deduce que la unidad del momento magnético en el Sistema Internacional es 1 A·m² (o, equivalentemente 1 J/T). Este valor es muy grande para las situaciones habituales. Por ejemplo, los momentos de las partículas elementales son cantidades del orden de un magnetón de Bohr
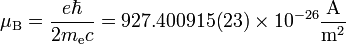
Este momento dipolar puede provenir de la existencia de una corriente localizada, o ser una propiedad intrínseca del sistema, asociada al espín.
3.1 Para una distribución de corriente
Al desarrollar el potencial vector magnético de una distribución localizada de corriente se obtiene que el primer término no nulo del desarrollo es el término dipolar. El valor de 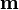 para una pequeña espira de corriente es
para una pequeña espira de corriente es
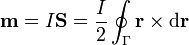
siendo 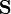 el vector superficie correspondiente a la curva.
el vector superficie correspondiente a la curva.
Las expresiones correspondientes a una distribución volumétrica y una superficial son
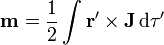
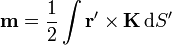
En caso de que tengamos varias distribuciones simultáneamente, el momento dipolar será la superposición de los momentos individuales.
3.1.1 Ejemplo: espira
- Para una espira plana, el momento magnético tiene por módulo el producto de la corriente por el área de la porción plana delimitado por la espira, y por sentido el normal a la superficie, según la regla de la mano derecha (si la corriente es positiva; en sentido opuesto en caso contrario).
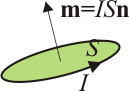
Como ejemplos elementales:
- Espira rectangular
- En el caso más sencillo, de una espira rectangular de lados a y b, el momento magnético será
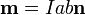
- Si consideramos los lados de la espira como vectores, esta expresión equivale a
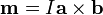
- Espira circular
- Para una espira circular el momento es
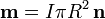
- Para una espira alabeada el vector superficie tiene por componentes las áreas de las proyecciones de la superficie sobre los planos coordenados. El momento magnético es igual a este vector multiplicado por la corriente.
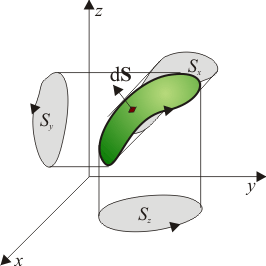
- Espira tridimensional
- Consideremos una espira alabeada formada por tres cuadrantes de circunferencia, de radio R que van de
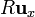 a
a 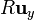 , de ahí a
, de ahí a 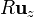 , y de vuelta a
, y de vuelta a 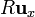 . Tal como se ve en artículo sobre el vector superficie, para esta superficie tenemos
. Tal como se ve en artículo sobre el vector superficie, para esta superficie tenemos
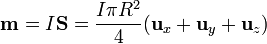
3.1.2 Ejemplo: esfera rotante
Un caso particular de corriente de volumen localizada en el espacio es el de una distribución de carga en rotación. Este modelo puede ayudar a describir el comportamiento de una partícula cargada, como un electrón, que se caracteriza por un momento angular (el espín), equivalente en ciertos aspectos a una rotación.
Supongamos una esfera de radio R, con una carga q distribuida uniformemente en el volumeny que gira en torno a un eje (que tomaremos como eje Z) con velocidad angular  . Para este sistema la densidad de corriente es, en esféricas
. Para este sistema la densidad de corriente es, en esféricas
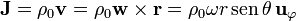

llevando esto a la integral resulta el momento magnético
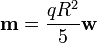
Lo más destacado de este resultado es que es proporcional a la velocidad angular de la partícula. Puesto que lo mismo ocurre con el momento angular
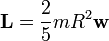
puede establecerse una relación de proporcionalidad entre el momento magnético y el momento angular
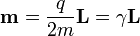
A la cantidad γ se la denomina razón giromagnética de la partícula.
3.2 Momentos intrínsecos
Además de los momentos asociados a corrientes, cada partícula elemental posee un momento dipolar intrínseco, proporcional a su espín, según la ley
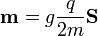
Esta ley es exactamente la misma que la que se cumple para una esfera en rotación. La única diferencia es la aparición de una constante de proporcionalidad adicional llamada factor-g (que para un electrón vale aproximadamente 2). Esto hace que, aunque un electrón no es una esfera rotante, se pueda hablar de su momento magnético como debido a su giro.
4 Acción de un campo externo sobre un dipolo
Las expresiones anteriores hablan del campo magnético causado por un dipolo magnético, pero no del efecto que un campo magnético externo produce sobre este dipolo.
Este efecto es análogo al caso de un dipolo eléctrico en el seno de un campo eléctrico. El dipolo experimenta una fuerza y un momento de una fuerza, y posee una cierta energía potencial
4.1 Fuerza
La fuerza experimentada por un dipolo magnético en un campo externo es
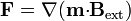
4.2 Par y momento
El momento sobre el dipolo se compone del momento de la fuerza aplicada, más un término intrínseco:
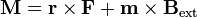
El segundo término representa un par intrínseco. Cuando hay fuerzas de rozamiento, de forma que el dipolo termina por quedarse quieto, el resultado es que el dipolo se alinea con el campo magnético, lo que constituye el fundamento de las brújulas.
4.3 Energía
Tanto la fuerza como el momento pueden derivarse de la energía de un dipolo en un campo externo
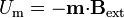
Esta energía es mínima cuando el dipolo apunta en la misma dirección y sentido que el campo aplicado sobre él.
5 Dipolos de Ampère y dipolos de Gilbert
Comparando la expresión del campo magnético con la con el campo eléctrico debido a un dipolo eléctrico
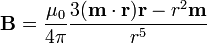

vemos que son formalmente idénticos. Según esto, una corriente eléctrica localizada produce en puntos alejados de ella un campo magnético idéntico al que producirían dos cargas (magnéticas, en este caso) muy próximas entre sí.
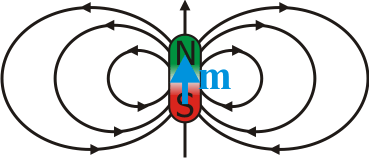
Esto permite dos visiones de los dipolos magnéticos (que sólo son percibidos por el campo que producen). Una, debida a Ampère, considera que todos los dipolos magnéticos son pequeñas espiras de corriente. La otra, concebida por Gilbert, supone la existencia de polos magnéticos separados dentro de cada dipolo.
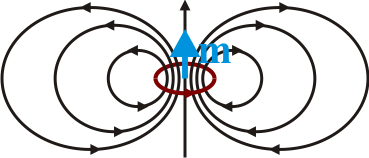
| 
|
| Modelo de dipolo de Ampère | Modelo de dipolo de Gilbert |
En el modelo de Gilbert, cada dipolo estaría formado por un polo norte (manantial de campo magnético) y un polo sur (sumidero). En el modelo de Ampère la espira define una cara norte (de la que salen las líneas de campo magnético) y una cara sur (por la que entran), obedeciendo la regla de la mano derecha.
Desde el punto de vista del campo que producen, ambos modelos son casi indistinguibles (sólo se diferencian en su valor justo en el punto donde se encuentra el dipolo, que no suele ser accesible.). Es un hecho, además, que existen momentos dipolares, como el debido al espín -en particular, el del neutrón- que no están producidos por espiras de corriente. El problema es saber si estos momentos dipolares se comportan como los del tipo de Ampère o los de Gilbert. La principal diferencia estriba en la relación con el momento angular. Un dipolo de Ampère debe llevar aparejado siempre un momento angular, mientras que un dipolo de Gilbert no tiene por qué. La experiencia muestra que todos los dipolos, microscópicos o macroscópicos, corresponden a dipolos de Ampère y pueden ser tratados como espiras de corriente.
Esta asociación con el momento angular se pone de manifiesto al considerar el efecto de un campo magnético externo sobre un dipolo. El momento de las fuerzas sobre un dipolo magnético en un campo uniforme es
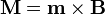
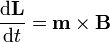
y, de acuerdo con la proporcionalidad entre el momento magnético y el momento angular resulta
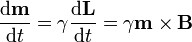
ecuación que predice que un dipolo magnético, en ausencia de fuerzas disipativas, no se orienta en la dirección del campo externo (como hace un dipolo eléctrico, o como haría un dipolo de Gilbert), sino que precesa en torno a el. Es éste fenómeno el que permite identificar a los momentos dipolares de las partículas como amperianos.