Segunda convocatoria 2017/18 (F2GIA)
De Laplace
(Diferencias entre revisiones)
(→Condensadores en asociación variable) |
(→Condensadores en asociación variable) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 1: | Línea 1: | ||
==[[Condensadores en asociación variable,_F2_GIA_(Sept,_2018)|Condensadores en asociación variable]]== | ==[[Condensadores en asociación variable,_F2_GIA_(Sept,_2018)|Condensadores en asociación variable]]== | ||
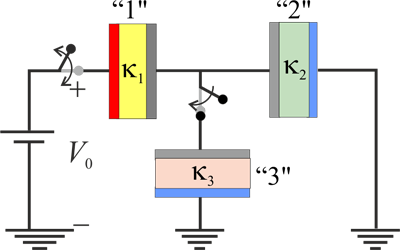
| - | + | e tienen tres condensadores de idéntica geometría, “1”, “2” y “3”, cuya capacidad eléctrica sería <math>C_0</math> si no hubiese ningún medio material dieléctrico separando los conductores. Sin embargo, están rellenos de sendos dieléctricos de constantes dieléctricas <math>\kappa_1</math>, <math>\kappa_2</math> y <math>\kappa_3</math>, respectivamente. Inicialmente se encuentran los tres descargados y los dos primeros están conectados en serie, con el conductor libre de “2” conectado al conductor de referencia o ''tierra''. Un generador electrostático de f.e.m. <math>V_0</math>, tiene su electrodo negativo conectado también al conductor de referencia. Se procede a conectar el electrodo positivo al conductor libre del condensador “1” para cargar la asociación en serie. Una vez realizado este paso, se desconecta el generador. Posteriormente, se conecta el conductor ''flotante'' de la asociación en serie formada por “1” y “2” a un conductor del condensador “3”, que tiene el otro conductor conectado a “tierra”. | |
[[Archivo:FII_gIA_18_19_bol_E3_7_0.png|right]] | [[Archivo:FII_gIA_18_19_bol_E3_7_0.png|right]] | ||
| - | # ¿Qué cantidad de carga eléctrica hay en cada uno de los conductores de “1” y “2” tras cargar la asociación en serie de | + | # ¿Qué cantidad de carga eléctrica hay en cada uno de los conductores de “1” y “2” tras cargar la asociación en serie de estos dos condensadores? ¿Cuál es el valor del potencial en el conductor ''flotante''? |
# ¿Qué valores de carga y potencial habrá en los conductores de cada condensador al conectar el condensador “3” al sistema, tal como se describe en el enunciado?¿Cómo ha cambiado la cantidad de energía almacenada al conectar dicho condensador? | # ¿Qué valores de carga y potencial habrá en los conductores de cada condensador al conectar el condensador “3” al sistema, tal como se describe en el enunciado?¿Cómo ha cambiado la cantidad de energía almacenada al conectar dicho condensador? | ||
| - | # Sean <math>\Delta V_1</math> | + | # Sean <math>\Delta V_1^\mathrm{max}</math>, <math>\Delta V_2^\mathrm{max}</math> y <math>\Delta V_3^\mathrm{max}</math> los valores de las diferencias de potencial máximas que pueden aplicarse a los respectivos condensadores “1”, “2” y “3” para que no se produzca la ruptura dieléctrica en cada uno de ellos. Obtenga las expresiones que permitan determinar cuál debe ser el valor máximo que puede tener <math>V_0</math>, en funcin de estos valores y de las constantes dieléctricas, para que en ningún momento del proceso descrito se produzca una ruptura dieléctrica en el sistema. Considere el caso particular en que <math>\kappa_1<\kappa_2<\kappa_3</math> y <math>\Delta V_1^\mathrm{max}<\Delta |
| - | V_2<\Delta V_3</math>: ¿cuál debe ser el valor máximo de <math>V_0</math>? | + | V_2^\mathrm{max}<\Delta V_3^\mathrm{max}</math>: ¿cuál debe ser el valor máximo de <math>V_0</math>? |
[[Categoría: Problemas de examen F2 GIA]] | [[Categoría: Problemas de examen F2 GIA]] | ||
última version al 10:54 29 mar 2019
Condensadores en asociación variable
e tienen tres condensadores de idéntica geometría, “1”, “2” y “3”, cuya capacidad eléctrica sería C0 si no hubiese ningún medio material dieléctrico separando los conductores. Sin embargo, están rellenos de sendos dieléctricos de constantes dieléctricas κ1, κ2 y κ3, respectivamente. Inicialmente se encuentran los tres descargados y los dos primeros están conectados en serie, con el conductor libre de “2” conectado al conductor de referencia o tierra. Un generador electrostático de f.e.m. V0, tiene su electrodo negativo conectado también al conductor de referencia. Se procede a conectar el electrodo positivo al conductor libre del condensador “1” para cargar la asociación en serie. Una vez realizado este paso, se desconecta el generador. Posteriormente, se conecta el conductor flotante de la asociación en serie formada por “1” y “2” a un conductor del condensador “3”, que tiene el otro conductor conectado a “tierra”.
- ¿Qué cantidad de carga eléctrica hay en cada uno de los conductores de “1” y “2” tras cargar la asociación en serie de estos dos condensadores? ¿Cuál es el valor del potencial en el conductor flotante?
- ¿Qué valores de carga y potencial habrá en los conductores de cada condensador al conectar el condensador “3” al sistema, tal como se describe en el enunciado?¿Cómo ha cambiado la cantidad de energía almacenada al conectar dicho condensador?
- Sean
, 
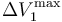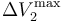y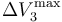 
los valores de las diferencias de potencial máximas que pueden aplicarse a los respectivos condensadores “1”, “2” y “3” para que no se produzca la ruptura dieléctrica en cada uno de ellos. Obtenga las expresiones que permitan determinar cuál debe ser el valor máximo que puede tener V0, en funcin de estos valores y de las constantes dieléctricas, para que en ningún momento del proceso descrito se produzca una ruptura dieléctrica en el sistema. Considere el caso particular en que κ1 < κ2 < κ3 y 
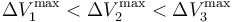: ¿cuál debe ser el valor máximo de V0?
