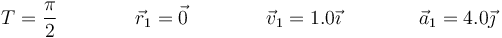Movimiento sobre un aro giratorio (GIE)
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Una partícula P se halla ensartada en un aro de radio <math>R=50\,<math>cm</math></math>. El aro se halla sujeto por uno de sus puntos a un motor en O. El motor p…') |
(→Enunciado) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Una partícula P se halla ensartada en un aro de radio <math>R=50\, | + | Una partícula P se halla ensartada en un aro de radio <math>R=50\,\mathrm{cm}</math>. El aro se halla sujeto por uno de sus puntos a un motor en O. El motor provoca que el aro gire en torno a O de forma que la posición del centro C forma un ángulo Ωt con el eje OX, siendo <math>\Omega=1\,\mathrm{rad}/\mathrm{s}</math>. El punto P se desplaza sobre el aro con rapidez constante respecto a éste, de forma que la distancia recorrida a lo largo del aro es <math>s=Vt</math> con <math>V=1\,\mathrm{m}/\mathrm{s}</math>. En <math>t=0</math> la partícula se halla en el punto diametralmente opuesto a O. |
<center>[[Archivo:aro-giratorio-particula.png|300px]]</center> | <center>[[Archivo:aro-giratorio-particula.png|300px]]</center> | ||
A partir de esta información determine: | A partir de esta información determine: | ||
| Línea 6: | Línea 6: | ||
# el radio y el centro de curvatura en <math>t=0</math>. | # el radio y el centro de curvatura en <math>t=0</math>. | ||
# el radio y el centro de curvatura en el momento en que la partícula llega a O. | # el radio y el centro de curvatura en el momento en que la partícula llega a O. | ||
| + | |||
==Posición, velocidad y aceleración== | ==Posición, velocidad y aceleración== | ||
Todo en las unidades fundamentales del SI | Todo en las unidades fundamentales del SI | ||
| Línea 21: | Línea 22: | ||
<center><math>T=\frac{\pi}{2}\qquad\qquad\vec{r}_1=\vec{0}\qquad\qquad \vec{v}_1=1.0\vec{\imath}\qquad\qquad \vec{a}_1=4.0\vec{\jmath}</math></center> | <center><math>T=\frac{\pi}{2}\qquad\qquad\vec{r}_1=\vec{0}\qquad\qquad \vec{v}_1=1.0\vec{\imath}\qquad\qquad \vec{a}_1=4.0\vec{\jmath}</math></center> | ||
| | ||
| - | <center><math>\vec{N}=\vec{\jmath}\qquad\qquad R=\frac{1.0^2}{4}=0.25\qquad\qquad \vec{r}_c=0.25\vec{\jmath}</math></center> | + | <center><math>\vec{N}=\vec{\jmath}\qquad\qquad R=\frac{1.0^2}{4.0}=0.25\qquad\qquad \vec{r}_c=0.25\vec{\jmath}</math></center> |
<center>[[Archivo:aro-giratorio-gif.gif]]</center> | <center>[[Archivo:aro-giratorio-gif.gif]]</center> | ||
última version al 16:03 19 oct 2019
Contenido |
1 Enunciado
Una partícula P se halla ensartada en un aro de radio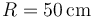 
. El aro se halla sujeto por uno de sus puntos a un motor en O. El motor provoca que el aro gire en torno a O de forma que la posición del centro C forma un ángulo Ωt con el eje OX, siendo 
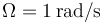. El punto P se desplaza sobre el aro con rapidez constante respecto a éste, de forma que la distancia recorrida a lo largo del aro es s = Vt con 
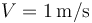. En t = 0 la partícula se halla en el punto diametralmente opuesto a O.
A partir de esta información determine:
- la posición, velocidad y aceleración de P como función del tiempo, respecto a los ejes indicados en la figura.
- el radio y el centro de curvatura en t = 0.
- el radio y el centro de curvatura en el momento en que la partícula llega a O.
2 Posición, velocidad y aceleración
Todo en las unidades fundamentales del SI
2.1 Posición
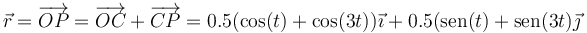
2.2 Velocidad
2.3 Aceleración
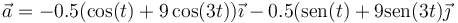
3 Centro y radio de curvatura en t=0
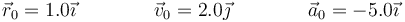
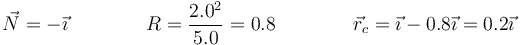
4 Centro y radio de curvatura en O
