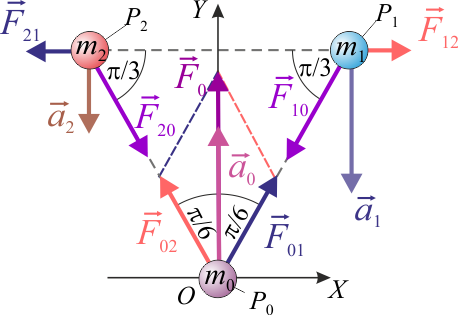
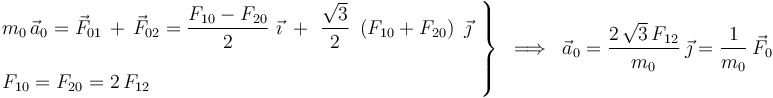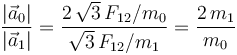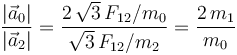Fuerzas de interacción y aceleraciones en sistema de tres partículas, F1 GIA (Ene, 2018)
De Laplace
(→Relación entre aceleraciones de P_1 y P_2) |
(→Enunciado) |
||
| (11 ediciones intermedias no se muestran.) | |||
| Línea 6: | Línea 6: | ||
[[Categoría:Problemas de Dinámica del Punto F1 GIA]] | [[Categoría:Problemas de Dinámica del Punto F1 GIA]] | ||
| + | [[Categoría:Problemas de examen F1 GIA]] | ||
==Solución== | ==Solución== | ||
| Línea 24: | Línea 25: | ||
Obtenemos las expresiones de las aceleraciones de estas partículas en el instante considerado y en términos de las intensidades <math>F_{ij}</math> de la fuerzas que actúan sobre ellas: | Obtenemos las expresiones de las aceleraciones de estas partículas en el instante considerado y en términos de las intensidades <math>F_{ij}</math> de la fuerzas que actúan sobre ellas: | ||
| - | <center><math>m_1\!\ \vec{a}_1=-m_1\!\ a_1\!\ \vec{\jmath}=\left(F_{12}-\frac{F_{10}}{2}\right)\ \vec{\imath} | + | <center><math>m_1\!\ \vec{a}_1=-m_1\!\ a_1\!\ \vec{\jmath}=\left(F_{12}-\frac{F_{10}}{2}\right)\ \vec{\imath}\ -\ \frac{\sqrt{3}}{2}\ F_{10}\ \vec{\jmath}=\vec{F}_{12}\!\ +\!\ \vec{F}_{10}\;\; \Longleftrightarrow \;\; \left\{\begin{array}{l}\displaystyle F_{10}=2\!\ F_{12}\\ \\ \displaystyle a_1=\frac{\sqrt{3}\!\ F_{10}}{2\!\ m_1}\end{array}\right. </math></center> |
| - | <center><math>m_2\!\ \vec{a}_2=-m_2\!\ a_2\!\ \vec{\jmath}=\left(\frac{F_{20}}{2}-F_{12}\right)\!\ \vec{\imath} | + | |
| + | <center><math>m_2\!\ \vec{a}_2=-m_2\!\ a_2\!\ \vec{\jmath}=\left(\frac{F_{20}}{2}-F_{12}\right)\!\ \vec{\imath}\ -\ \frac{\sqrt{3}}{2}\ F_{20}\!\ \vec{\jmath}\;=\vec{F}_{20}\!\ +\!\ \vec{F}_{21} \Longleftrightarrow \;\; \left\{\begin{array}{l}\displaystyle F_{20}=2\!\ F_{12}\\ \\ \displaystyle a_2=\frac{\sqrt{3}\!\ F_{20}}{2\!\ m_2}\end{array}\right. </math></center> | ||
Por tanto, la relación entre las intensidades de las aceleraciones de estás partículas en el instante considerado, es... | Por tanto, la relación entre las intensidades de las aceleraciones de estás partículas en el instante considerado, es... | ||
<center><math>\frac{|\vec{a}_1|}{|\vec{a}_2|}=\frac{a_1}{a_2}=\frac{F_{10}/m_1}{F_{20}/m_2}\;\; \Longrightarrow</math>{{qquad}}<math style="border:solid violet 2px;padding:10px">\frac{|\vec{a}_1|}{|\vec{a}_2|}=\frac{2\!\ F_{12}/m_1}{2\!\ F_{12}/m_2}=\frac{m_2}{m_1}</math></center> | <center><math>\frac{|\vec{a}_1|}{|\vec{a}_2|}=\frac{a_1}{a_2}=\frac{F_{10}/m_1}{F_{20}/m_2}\;\; \Longrightarrow</math>{{qquad}}<math style="border:solid violet 2px;padding:10px">\frac{|\vec{a}_1|}{|\vec{a}_2|}=\frac{2\!\ F_{12}/m_1}{2\!\ F_{12}/m_2}=\frac{m_2}{m_1}</math></center> | ||
| + | |||
| + | ===Aceleración de la partícula <math>P_0</math>=== | ||
| + | Aplicando las leyes de la Dinámica en esta partícula, se tendrá: | ||
| + | |||
| + | <center><math>\left.\begin{array}{l}\displaystyle m_0\!\ \vec{a}_0=\vec{F}_{01}\!\ +\!\ \vec{F}_{02}=\frac{F_{10}-F_{20}}{2}\ \vec{\imath}\ +\ \frac{\sqrt{3}}{2}\ \left(F_{10}+F_{20}\right)\ \vec{\jmath}\\ \\ | ||
| + | \displaystyle F_{10}=F_{20}=2\!\ F_{12} | ||
| + | \end{array}\right\}\;\; \Longrightarrow \;\; \vec{a}_0=\frac{2\!\ \sqrt{3}\!\ F_{12}}{m_0}\ \vec{\jmath}=\frac{1}{m_0}\ \vec{F}_0</math></center> | ||
| + | |||
| + | |||
| + | [[Archivo:f1_gIA_ex1ac_17_18_e2_2.png|right]]Por tanto, las relaciones de esta aceleración con las de las otra partículas son: | ||
| + | |||
| + | |||
| + | <center><math style="border:solid blue 2px;padding:10px">\frac{|\vec{a}_0|}{|\vec{a}_1|}=\frac{2\!\ \sqrt{3}\!\ F_{12}/m_0}{\sqrt{3}\!\ F_{12}/m_1}=\frac{2\!\ m_1}{m_0}</math>{{qquad}}{{qquad}}</center> | ||
| + | |||
| + | |||
| + | <center><math style="border:solid red 2px;padding:10px">\frac{|\vec{a}_0|}{|\vec{a}_2|}=\frac{2\!\ \sqrt{3}\!\ F_{12}/m_0}{\sqrt{3}\!\ F_{12}/m_2}=\frac{2\!\ m_1}{m_0}</math> </center> | ||
última version al 12:05 20 ago 2018
Contenido |
1 Enunciado
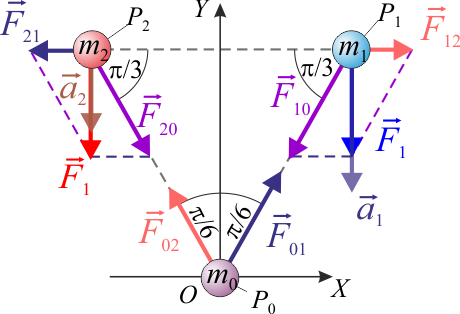
Tres partículas PO, P1 y P2, de masas conocidas con valores m0, m1 y m2, respectivamente, interaccionan entre sí de manera que la fuerza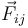 que la partícula Pj ejerce sobre la Pi, tiene la dirección del segmento
que la partícula Pj ejerce sobre la Pi, tiene la dirección del segmento 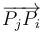 (es decir,
(es decir, 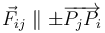 ). En un determinado instante, las partículas ocupan los vértices de un triángulo equilátero; se adopta un sistema de referencia cartesiano OXYZ tal que dicho triángulo está contenido en plano OXY, con el segmento
). En un determinado instante, las partículas ocupan los vértices de un triángulo equilátero; se adopta un sistema de referencia cartesiano OXYZ tal que dicho triángulo está contenido en plano OXY, con el segmento 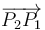 paralelo al eje OX, y la partícula P0 en el punto O. En dicho instante, las aceleraciones de las partículas P1 y P2 tiene igual dirección y sentido, siendo paralelas y opuestas al eje OY; es decir
paralelo al eje OX, y la partícula P0 en el punto O. En dicho instante, las aceleraciones de las partículas P1 y P2 tiene igual dirección y sentido, siendo paralelas y opuestas al eje OY; es decir 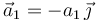 y
y 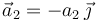 , respectivamente, con
, respectivamente, con 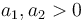
- Determine qué relación verifican los módulos de dichas aceleraciones,
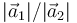 , en función de las masas de las partículas.
, en función de las masas de las partículas.
- Determine la dirección y el sentido de la aceleración
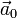 de la partícula P0. ¿Cuánto vale su módulo en relación con los módulos de las aceleraciones de P1 y P2?
de la partícula P0. ¿Cuánto vale su módulo en relación con los módulos de las aceleraciones de P1 y P2?
2 Solución
Para resolver este ejercicio sólo es necesario aplicar las leyes de Dinámica para el punto material. La segunda ley de Newton y el principio de superposición establecen que la aceleración instantánea 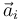 de la partícula Pi multiplicada por su masa inercial, es igual a la resultante de
de la partícula Pi multiplicada por su masa inercial, es igual a la resultante de 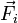 de las fuerzas que actúan en dicho instante sobre la partícula. Además, el principio de acción y reacción establece que las fuerzas de interacción entre cada par de partículas son opuestas; además, en el ejercicio propuesto, estas fuerzas son colineales con la recta que pasa por cada par de puntos:
de las fuerzas que actúan en dicho instante sobre la partícula. Además, el principio de acción y reacción establece que las fuerzas de interacción entre cada par de partículas son opuestas; además, en el ejercicio propuesto, estas fuerzas son colineales con la recta que pasa por cada par de puntos:
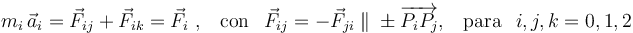
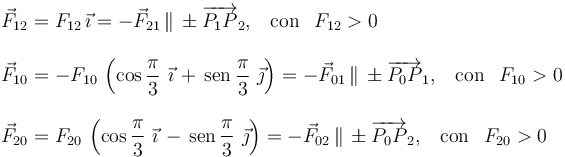
Nótese que no tenemos información acerca de la naturaleza de las fuerzas de interacción mutua 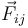 , por lo que desconocemos el valor de sus intensidades o módulos, Fij. Sin embargo, no necesitamos esta información para resolver el ejercicio propuesto:
, por lo que desconocemos el valor de sus intensidades o módulos, Fij. Sin embargo, no necesitamos esta información para resolver el ejercicio propuesto:
2.1 Relación entre aceleraciones de P1 y P2
Obtenemos las expresiones de las aceleraciones de estas partículas en el instante considerado y en términos de las intensidades Fij de la fuerzas que actúan sobre ellas:
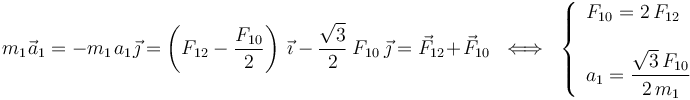
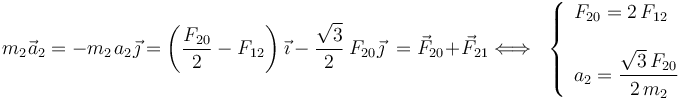
Por tanto, la relación entre las intensidades de las aceleraciones de estás partículas en el instante considerado, es...

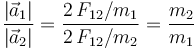
2.2 Aceleración de la partícula P0
Aplicando las leyes de la Dinámica en esta partícula, se tendrá: