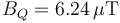Tres hilos paralelos (GIE)
De Laplace
(Página creada con '==Enunciado== Se dispone de tres cables de cobre (<math>\sigma=5.96\times 10^7 \mathrm{S}/\mathrm{m}</math>) de 40m cada uno, dos de ellos de diámetro 1mm y el otro de diámetr…') |
|||
| (4 ediciones intermedias no se muestran.) | |||
| Línea 5: | Línea 5: | ||
# el módulo del campo magnético en los puntos P y Q situados respectivamente en el punto medio entre los hilos 1 y 2, y entre los hilos 2 y 3. | # el módulo del campo magnético en los puntos P y Q situados respectivamente en el punto medio entre los hilos 1 y 2, y entre los hilos 2 y 3. | ||
<center>[[Archivo:tres-hilos-paralelos.png|500px]]</center> | <center>[[Archivo:tres-hilos-paralelos.png|500px]]</center> | ||
| + | ==Intensidad y densidad de corriente== | ||
| + | La resistencia de cada cable es | ||
| + | |||
| + | <center><math>R_2=\frac{\ell}{\sigma S}=\frac{40\,\mathrm{m}}{5.96\times 10^7\mathrm{S}/\mathrm{m}\times\pi\times (0.002\,\mathrm{m}/2)^2}=0.214\,\Omega=\frac{R_1}{4}</math></center> | ||
| + | | ||
| + | <center><math>R_1=R_3=\frac{\ell}{\sigma S}=\frac{40\,\mathrm{m}}{5.96\times 10^7\mathrm{S}/\mathrm{m}\times\pi\times (0.001\,\mathrm{m}/2)^2}=0.854\,\Omega=4R_2</math></center> | ||
| + | |||
| + | Las resistencias 2 y 3 están en paralelo entre sí | ||
| + | |||
| + | <center><math>R_{23}=\frac{R_2R_3}{R_2+R_3}=\frac{4R_2^2}{5R_2}=\frac{4}{5}R_2=0.171\,\Omega</math></center> | ||
| + | |||
| + | y esta está en serie con la 1 | ||
| + | |||
| + | <center><math>R_{123}=R_1+R_{23}=4R_2+\frac{4}{5}R_2=\frac{24}{5}R_2=1.03\,\Omega</math></center> | ||
| + | ===Intensidad de corriente=== | ||
| + | |||
| + | La corriente que recorre el hilo 1 es toda la corriente | ||
| + | |||
| + | <center><math>I_1=\frac{V_0}{R_{123}}=11.7\,\mathrm{A}</math></center> | ||
| + | |||
| + | Esta corriente se reparte entre los hilos 2 y 3 de forma inversamente proporcional a su resistencia | ||
| + | |||
| + | <center><math>I_2=\frac{R_3}{R_2+R_3}I_1=\frac{4}{5}I_1=9.36\,\mathrm{A}\qquad\qquad I_3=\frac{1}{5}I_1=2.34\,\mathrm{A}</math></center> | ||
| + | ===Densidad de corriente=== | ||
| + | |||
| + | Cada intensidad de corriente se reparte uniformemente por su sección | ||
| + | |||
| + | <center><math>J_1=\frac{I_1}{S_1}=\frac{11.7}{\pi\times (0.001\,\mathrm{m}/2)^2}=1.49\times 10^7\,\frac{\mathrm{A}}{\mathrm{m}^2}</math></center> | ||
| + | | ||
| + | <center><math>J_2=\frac{I_2}{S_2}=\frac{9.36}{\pi\times (0.002\,\mathrm{m}/2)^2}=2.98\times 10^6\,\frac{\mathrm{A}}{\mathrm{m}^2}</math></center> | ||
| + | | ||
| + | <center><math>J_2=\frac{I_2}{S_2}=\frac{2.34}{\pi\times (0.001\,\mathrm{m}/2)^2}=2.98\times 10^6\,\frac{\mathrm{A}}{\mathrm{m}^2}</math></center> | ||
| + | |||
| + | Vemos que las densidades den los cables 2 y 3 son iguales. la del cable 1 es la quinta parte de la del 2 y 3. | ||
| + | |||
| + | la densidades de corriente son vectores. En este caso, la densidad en 1 tiene el sentido de izquierda a derecha y en 2 y 3 de derecha a izquierda. | ||
| + | ==Potencia disipada== | ||
| + | La potencia disipada por efecto Joule se puede calcular de diferentes maneras | ||
| + | |||
| + | <center><math>P=\sum_i I_i^2 R_i\,</math></center> | ||
| + | | ||
| + | <center><math>P=I_1^2 R_{123}\,</math></center> | ||
| + | | ||
| + | <center><math>P=I_1V_1+I_2V_2+I_3V_3\,</math></center> | ||
| + | El resultado es | ||
| + | <center><math>P=I_1 V_0+0+0=140\,\mathrm{W}\,</math></center> | ||
| + | ==Campo magnético== | ||
| + | El campo magnético debido a un hilo rectilíneo de gran longitud es de la forma | ||
| + | |||
| + | <center><math>\vec{B}=\frac{\mu_0I}{2\pi\rho}\vec{u}_\theta</math></center> | ||
| + | |||
| + | En este caso, si tomamos <math>\vec{k}</math> como el vector normal al plano de la figura y hacia afuera, el campo en P y Q será la suma de los campos debidos a cada hilo, con un signo dependiente de si va en el sentido <math>+\vec{k}</math> o <math>-\vec{k}</math> | ||
| + | ===En P=== | ||
| + | En P el campo de los tres hilos va en el sentido de <math>-\vec{k}</math>, por lo que | ||
| + | |||
| + | <center><math>\vec{B}_P=\frac{\mu_0}{4\pi}\left(\frac{I_1}{d_1}+\frac{I_2}{d_2}+\frac{I_3}{d_3}\right)(-\vec{k})=-2\times 10^{-7}\left(\frac{11.7}{0.1}+\frac{9.36}{0.1}+\frac{2.34}{0.3}\right)\vec{k} = -43.6\,\mu\mathrm{T}\vec{k}</math></center> | ||
| + | |||
| + | En módulo | ||
| + | |||
| + | <center><math>B_P=43.6\,\mu\mathrm{T}</math></center> | ||
| + | ===En Q=== | ||
| + | En Q el campo de hilos 1 y 3 va en el sentido de <math>-\vec{k}</math>, pero el 2 va en el de <math>+\vec{k}</math> por lo que | ||
| + | |||
| + | <center><math>\vec{B}_Q=\frac{\mu_0}{4\pi}\left(-\frac{I_1}{d_1}+\frac{I_2}{d_2}-\frac{I_3}{d_3}\right)\vec{k}=2\times 10^{-7}\left(-\frac{11.7}{0.3}+\frac{9.36}{0.1}-\frac{2.34}{0.1}\right)\vec{k} = +6.24,\mu\mathrm{T}\vec{k}</math></center> | ||
| + | |||
| + | En módulo | ||
| + | |||
| + | <center><math>B_Q=6.24\,\mu\mathrm{T}</math></center> | ||
última version al 19:48 29 may 2018
Contenido |
1 Enunciado
Se dispone de tres cables de cobre (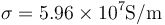
) de 40m cada uno, dos de ellos de diámetro 1mm y el otro de diámetro 2mm (siendo la sección circular en los 3). Se conectan como indica el esquema, estando los hilos situados a una distancia de 20cm, con el más grueso en medio. El cable de unión entre los hilos puede considerarse un cortocircuito. La fuente de tensión conectada al hilo 1 fija un voltaje de 12V. Calcule…
- la intensidad de corriente y la densidad de corriente que circula por cada hilo.
- la potencia disipada en el sistema por efecto Joule
- el módulo del campo magnético en los puntos P y Q situados respectivamente en el punto medio entre los hilos 1 y 2, y entre los hilos 2 y 3.
2 Intensidad y densidad de corriente
La resistencia de cada cable es
Las resistencias 2 y 3 están en paralelo entre sí
y esta está en serie con la 1
2.1 Intensidad de corriente
La corriente que recorre el hilo 1 es toda la corriente
Esta corriente se reparte entre los hilos 2 y 3 de forma inversamente proporcional a su resistencia
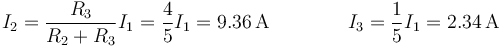
2.2 Densidad de corriente
Cada intensidad de corriente se reparte uniformemente por su sección
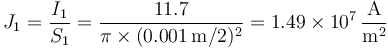
Vemos que las densidades den los cables 2 y 3 son iguales. la del cable 1 es la quinta parte de la del 2 y 3.
la densidades de corriente son vectores. En este caso, la densidad en 1 tiene el sentido de izquierda a derecha y en 2 y 3 de derecha a izquierda.
3 Potencia disipada
La potencia disipada por efecto Joule se puede calcular de diferentes maneras
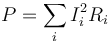
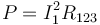
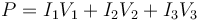
El resultado es
4 Campo magnético
El campo magnético debido a un hilo rectilíneo de gran longitud es de la forma
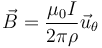
En este caso, si tomamos 
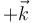como el vector normal al plano de la figura y hacia afuera, el campo en P y Q será la suma de los campos debidos a cada hilo, con un signo dependiente de si va en el sentido 
o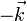 
4.1 En P
En P el campo de los tres hilos va en el sentido de 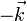, por lo que
En módulo
4.2 En Q
En Q el campo de hilos 1 y 3 va en el sentido de 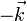, pero el 2 va en el de 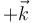por lo que
En módulo
