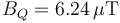Tres hilos paralelos (GIE)
De Laplace
Contenido |
1 Enunciado
Se dispone de tres cables de cobre (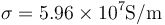
) de 40m cada uno, dos de ellos de diámetro 1mm y el otro de diámetro 2mm (siendo la sección circular en los 3). Se conectan como indica el esquema, estando los hilos situados a una distancia de 20cm, con el más grueso en medio. El cable de unión entre los hilos puede considerarse un cortocircuito. La fuente de tensión conectada al hilo 1 fija un voltaje de 12V. Calcule…
- la intensidad de corriente y la densidad de corriente que circula por cada hilo.
- la potencia disipada en el sistema por efecto Joule
- el módulo del campo magnético en los puntos P y Q situados respectivamente en el punto medio entre los hilos 1 y 2, y entre los hilos 2 y 3.
2 Intensidad y densidad de corriente
La resistencia de cada cable es
Las resistencias 2 y 3 están en paralelo entre sí
y esta está en serie con la 1
2.1 Intensidad de corriente
La corriente que recorre el hilo 1 es toda la corriente
Esta corriente se reparte entre los hilos 2 y 3 de forma inversamente proporcional a su resistencia
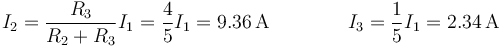
2.2 Densidad de corriente
Cada intensidad de corriente se reparte uniformemente por su sección
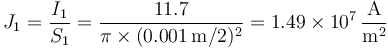
Vemos que las densidades den los cables 2 y 3 son iguales. la del cable 1 es la quinta parte de la del 2 y 3.
la densidades de corriente son vectores. En este caso, la densidad en 1 tiene el sentido de izquierda a derecha y en 2 y 3 de derecha a izquierda.
3 Potencia disipada
La potencia disipada por efecto Joule se puede calcular de diferentes maneras
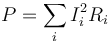
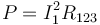
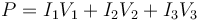
El resultado es
4 Campo magnético
El campo magnético debido a un hilo rectilíneo de gran longitud es de la forma
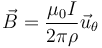
En este caso, si tomamos 
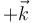como el vector normal al plano de la figura y hacia afuera, el campo en P y Q será la suma de los campos debidos a cada hilo, con un signo dependiente de si va en el sentido 
o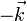 
4.1 En P
En P el campo de los tres hilos va en el sentido de 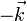, por lo que
En módulo
4.2 En Q
En Q el campo de hilos 1 y 3 va en el sentido de 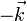, pero el 2 va en el de 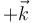por lo que
En módulo
