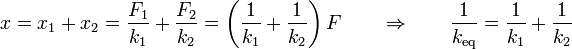Entrar Página Discusión Historial Go to the site toolbox

Dinámica del oscilador armónico (GIE)

De Laplace

(Diferencias entre revisiones)
(→Resortes en serie)
 
(2 ediciones intermedias no se muestran.)
Línea 108: Línea 108:
Sea <math>\ell</math> la longitud que adquieren ambos resortes (que será necesariamente la misma para los dos).  
Sea <math>\ell</math> la longitud que adquieren ambos resortes (que será necesariamente la misma para los dos).  
-
<center><math>l = l_1 = l_2\,</math></center>
+
<center><math>\ell = \ell_1 = \ell_2\,</math></center>
La ecuación de movimiento para la masa es
La ecuación de movimiento para la masa es
Línea 161: Línea 161:
Supongamos ahora dos resortes ideales de constantes <math>k_1</math> y <math>k_2</math> y longitudes en reposo <math>\ell_{10}</math> y <math>\ell_{20}</math> conectados uno a continuación del otro y una masa que cuelga del extremo inferior de la asociación. En este caso, la masa se encuentra a una distancia del techo
Supongamos ahora dos resortes ideales de constantes <math>k_1</math> y <math>k_2</math> y longitudes en reposo <math>\ell_{10}</math> y <math>\ell_{20}</math> conectados uno a continuación del otro y una masa que cuelga del extremo inferior de la asociación. En este caso, la masa se encuentra a una distancia del techo
-
<center><math>l = l_1 + l_2\,</math></center>
+
<center><math>\ell = \ell_1 + \ell_2\,</math></center>
Para escribir las ecuaciones de movimiento, consideraremos temporalmente que en el punto de unión de los dos muelles se encuentra una pequeña masa <math>m_0</math>, que luego haremos tender a cero.
Para escribir las ecuaciones de movimiento, consideraremos temporalmente que en el punto de unión de los dos muelles se encuentra una pequeña masa <math>m_0</math>, que luego haremos tender a cero.
Línea 167: Línea 167:
La segunda ley de Newton aplicada a la masa <math>m</math> nos da
La segunda ley de Newton aplicada a la masa <math>m</math> nos da
-
<center><math>ma = -k_2\left(l_2-\ell_{20}\right)+mg\,</math></center>
+
<center><math>ma = -k_2\left(\ell_2-\ell_{20}\right)+mg\,</math></center>
Nótese que sobre esta masa no actúa el resorte 1, ya que no se encuentra conectado a la masa y no ejerce fuerzas a distancia. Esto nos permite expresar la elongación del muelle inferior en función del peso y la aceleración de la masa
Nótese que sobre esta masa no actúa el resorte 1, ya que no se encuentra conectado a la masa y no ejerce fuerzas a distancia. Esto nos permite expresar la elongación del muelle inferior en función del peso y la aceleración de la masa
-
<center><math>\Delta l_2 = l_2-\ell_{20} = \frac{F_2}{k_2}=\frac{1}{k_2}(mg-ma)</math></center>
+
<center><math>\Delta \ell_2 = \ell_2-\ell_{20} = \frac{F_2}{k_2}=\frac{1}{k_2}(mg-ma)</math></center>
Sobre la masa intermedia actúan los dos resortes, cada uno tirando en un sentido, de forma que
Sobre la masa intermedia actúan los dos resortes, cada uno tirando en un sentido, de forma que
-
<center><math>m_0a_0 = -k_1(l_1-\ell_{10})+k_2(l_2-\ell_{20})+m_0g\,</math></center>
+
<center><math>m_0a_0 = -k_1(\ell_1-\ell_{10})+k_2(\ell_2-\ell_{20})+m_0g\,</math></center>
Ahora bien, si la masa intermedia es despreciable, <math>m_0\to 0</math> y la ecuación se reduce a
Ahora bien, si la masa intermedia es despreciable, <math>m_0\to 0</math> y la ecuación se reduce a
-
<center><math>-k_1(l_1-\ell_{10}) = -k_2(l_2-\ell_{20})\,</math></center>
+
<center><math>-k_1(\ell_1-\ell_{10}) = -k_2(\ell_2-\ell_{20})\,</math></center>
esto es, los dos resortes ejercen la misma fuerza
esto es, los dos resortes ejercen la misma fuerza
Línea 187: Línea 187:
Esto nos permite calcular la elongación del muelle superior
Esto nos permite calcular la elongación del muelle superior
-
<center><math>\Delta l_1 = l_1-\ell_{10} = \frac{F_1}{k_1}=\frac{F_2}{k_1}=\frac{1}{k_1}(mg-ma)</math></center>
+
<center><math>\Delta \ell_1 = \ell_1-\ell_{10} = \frac{F_1}{k_1}=\frac{F_2}{k_1}=\frac{1}{k_1}(mg-ma)</math></center>
 +
 
 +
Dicho de otra forma, del muelle superior cuelga el inferior (sin masa) y la pesa que cuelga de éste. Por tanto se estira lo mismo que si colgara directamente la masa.
Sumando las dos elongaciones obtenemos la elongación total
Sumando las dos elongaciones obtenemos la elongación total
-
<center><math>l-(\ell_{10}+\ell_{20}) = \Delta l = \Delta l_1 + \Delta l_2 = \left(\frac{1}{k_1}+\frac{1}{k_2}\right)(mg-ma)</math></center>
+
<center><math>\ell-(\ell_{10}+\ell_{20}) = \Delta \ell = \Delta \ell_1 + \Delta \ell_2 = \left(\frac{1}{k_1}+\frac{1}{k_2}\right)(mg-ma)</math></center>
De aquí sacamos la posición de equilibrio, que se alcanza cuando la aceleración es nula
De aquí sacamos la posición de equilibrio, que se alcanza cuando la aceleración es nula

última version al 15:26 30 oct 2017

Contenido

1 Ley de Hooke

Todos los materiales sólidos poseen una cierta elasticidad, lo que implica que si se les aplica una pequeña fuerza se comprimen o estiran, según el sentido de la fuerza. Cuando ésta es débil, la deformación es aproximadamente proporcional a la fuerza aplicada. Para el caso de una barra que se estira o comprimer longitudinalmente

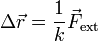
\Delta \vec{r} = \frac{1}{k}\vec{F}_\mathrm{ext}

Por la tercera ley de Newton, esto quiere decir que la barra ejerce una fuerza igual y de sentido contrario y por tanto proporcional a la deformación

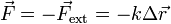
\vec{F}=-\vec{F}_\mathrm{ext}=-k\Delta\vec{r}

Esta es la conocida como ley de Hooke. Nos dice que cuando se estira o comprime un material elástico, éste ejerce una fuerza proporcional a la deformación efectuada y que se opone a ella (por lo que se denomina fuerza recuperadora).

Se trata de una aproximación válida solo para deformaciones y fuerzas pequeñas. Para deformaciones moderadas, la fuerza recuperadora deja de ser proporcional a la deformación. Para fuerzas grandes la fuerza ya no es capaz de devolver el sólido al estado inicial, con lo que la deformación es permanente (régimen plástico). Mayores deformaciones llegan a producir la ruptura del material.

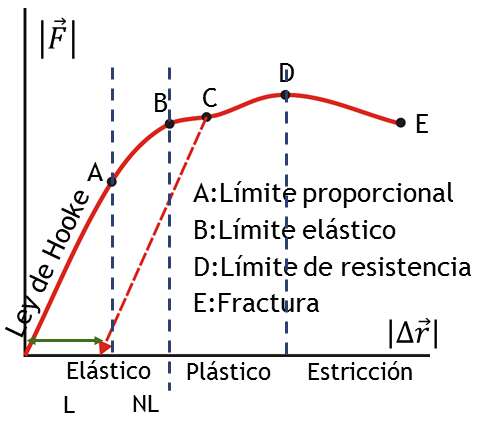
Archivo:Regimenes-resorte.png

La constante k que aparece en la ley de Hooke se denomina constante de recuperación o simplemente constante del muelle (por ser los muelles o resortes ejemplos típocs de aplicación de la ley).

Para el caso de una barra o resorte horizontal, podemos emplear cantidades escalares y escribir

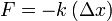
F = - k\,(\Delta x)

siendo Δx la diferencia entre la longitud instantánea, 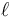\ell y la longitud que tiene en ausencia de fuerza, conocida como longitud en reposo o longitud natural, 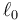\ell_0, de forma que la ley de Hooke queda

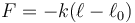
F = -k(\ell-\ell_0)\,

La longitud 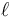\ell puede ser tanto mayor como menor que \ell_0.

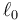2 Dinamómetros

La ley de Hooke es la base de los dinamómetros más sencillos. Estos aparatos miden una fuerza simplemente considerando la posición de equilibrio de un resorte elástico.

De acuerdo con la segunda ley de Newton, si sobre una partícula en el extremo de un resorte se aplica una fuerza externa Fext, se cumplirá

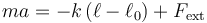
ma =-k\left(\ell-\ell_0\right)+F_\mathrm{ext}\,

Si el resorte está en equilibrio, la aceleración es nula y

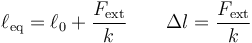
\ell_\mathrm{eq} = \ell_0 + \frac{F_\mathrm{ext}}{k}\qquad \Delta l = \frac{F_\mathrm{ext}}{k}

con lo cual, midiendo el estiramiento, obtenemos la fuerza.

En el caso de que se trate de un resorte suspendido verticalmente, la fuerza externa es el peso de la masa colgada de él, de forma que la ecuación anterior queda

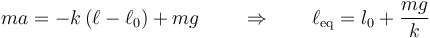
ma = -k\left(\ell-\ell_0\right) + mg\,\qquad\Rightarrow\qquad \ell_\mathrm{eq}=l_0+\frac{mg}{k}

El estiramiento es proporcional a la masa, lo que constituye el fundamento de la mayoría de las balanzas.

Teniendo en cuenta la posición de equilibrio, la ley de Hooke puede escribirse

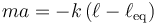
ma = -k\left( \ell-\ell_\mathrm{eq}\right)

que nos dice que la dinámica de un resorte suspendido verticalmente es idéntica a la de uno horizontal, sin más que cambiar la longitud en reposo por la longitud de equilibrio (igual a la de reposo más una cierta cantidad proporcional a la masa colgada).

3 Movimiento de un oscilador armónico

3.1 Rectilíneo

Si tenemos un resorte gobernado la ley de Hooke, su ecuación de movimiento es

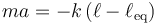
ma = -k\left(\ell-\ell_\mathrm{eq}\right)\,

Si medimos la posición no desde el extremo del resorte sino desde la posición de equilibrio

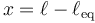
x = \ell-\ell_\mathrm{eq}\,

esta ecuación se reduce a

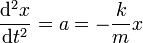
\frac{\mathrm{d}^2x}{\mathrm{d}t^2} = a = -\frac{k}{m}x

Si hacemos

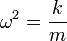
\omega^2 = \frac{k}{m}

vemos que la solución de esta ecuación es un movimiento armónico simple, con solución general

x = x_0\cos(\omega t) +\frac{v_0}{\omega}\mathrm{sen}(\omega t) = A\cos(\omega t-\varphi)
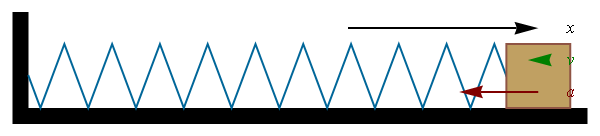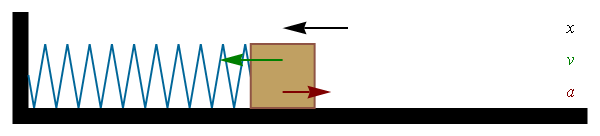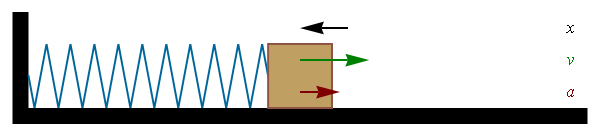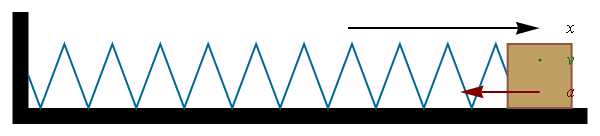
Archivo:Muelle.gif

El periodo de las oscilaciones depende de la masa y la constante del muelle

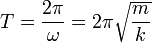
T = \frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}

Esto quiere decir que para conseguir el doble de periodo debemos multiplicar por 4 la masa suspendida. La frecuencia natural de las oscilaciones vale

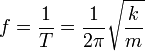
f = \frac{1}{T}=\frac{1}{2\pi}\sqrt{\frac{k}{m}}

La amplitud y la constante de fase dependen de la posición y la velocidad iniciales.

3.2 Tridimensional

La ley de Hooke no solo se aplica a resortes lineales, sino que existen numerosos sistemas que, en las proximidades de un punto de equilibrio, obedecen la ecuación de movimiento

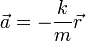
\vec{a}=-\frac{k}{m}\vec{r}

La solución de esta ecuación es la generalización del caso rectilíneo

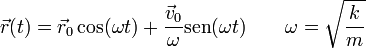
\vec{r}(t) = \vec{r}_0\cos(\omega t) + \frac{\vec{v}_0}{\omega}\mathrm{sen}(\omega t)\qquad \omega =\sqrt{\frac{k}{m}}

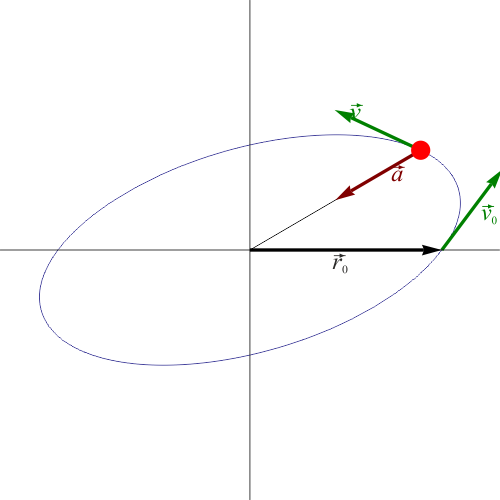
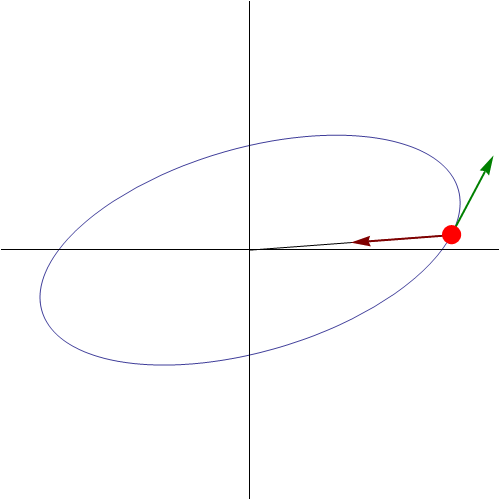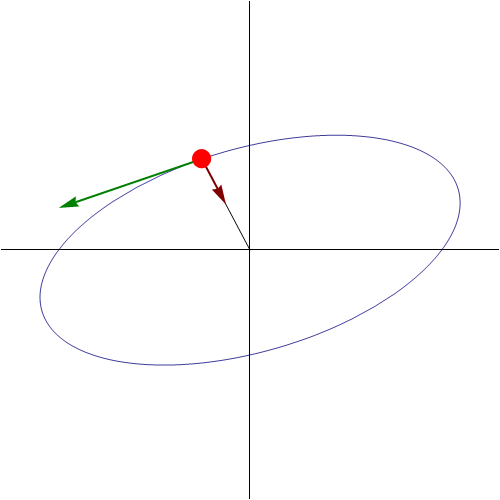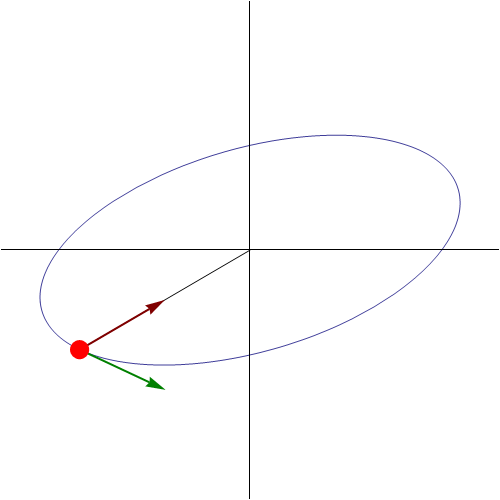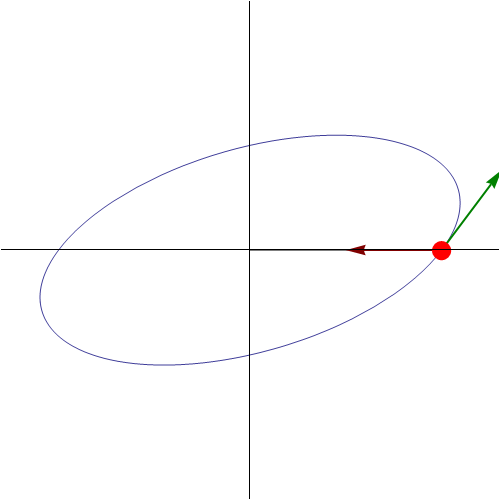
Sin embargo, a diferencia del caso rectilíneo, esto no se trata de un movimiento armónico simple, aunque lo parezca, sino que la partícula describe una elipse en torno al punto de equilibrio. Esta elipse se encuentra contenida en el plano definido por la posición y la velocidad iniciales.

Archivo:muelle2d.png    Archivo:muelle2d.gif

4 Asociaciones de osciladores

¿Qué sucede cuando colgamos un muelle de otro y una masa en el extremo del inferior? ¿Y sí ponemos una masa que cuelga estando sujeta a dos resortes simultáneamente? ¿Cuánto valen en esos casos la frecuencia de oscilación? ¿Cuál es la nueva posición de equilibrio?

4.1 Resortes en paralelo

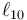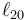Consideremos en primer lugar el caso de dos resortes de constantes k1 y k2 y longitudes en reposo \ell_{10} y \ell_{20}, que cuelgan del techo y una masa m suspendida de ambos muelles simultáneamente. ¿Cuál es la posición de equilibrio y con qué frecuencia oscila la masa?

Sea 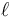\ell la longitud que adquieren ambos resortes (que será necesariamente la misma para los dos).

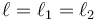
\ell = \ell_1 = \ell_2\,

La ecuación de movimiento para la masa es

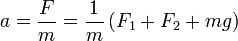
a = \frac{F}{m}=\frac{1}{m}\left(F_1+F_2+mg\right)

siendo F1 y F2 las fuerzas producidas por cada una de los resortes

F_1 = -k_1(\ell-\ell_{10})\qquad F_2 = -k_2(\ell-\ell_{20})

La posición de equilibrio nos la da el que la fuerza sea cero

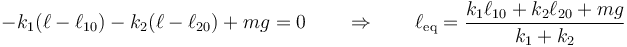
-k_1(\ell-\ell_{10}) - k_2(\ell-\ell_{20}) + mg = 0\qquad\Rightarrow\qquad \ell_\mathrm{eq} = \frac{k_1\ell_{10}+k_2\ell_{20}+mg}{k_1+k_2}

Podemos comprobar que en este resultado si 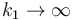k_1\to\infty (el primer muelle se hace infinitamente rígido)

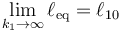
\lim_{k_1\to\infty}\ell_\mathrm{eq} = \ell_{10}

esto es, este resorte no se estira en absoluto. Igualmente si hacemos 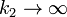k_2\to\infty, es el segundo muelle el que no se estira.

Definiendo la posición respecto a la de equilibrio

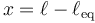
x = \ell-\ell_\mathrm{eq}\,

la ecuación de movimiento se convierte en

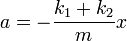
a = -\frac{k_1+k_2}{m}x

que nos dice que el muelle oscila en torno a su posición de equilibrio con una constante equivalente a la asociación que es la suma de las constantes individuales

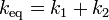
k_\mathrm{eq}=k_1+k_2\,

de forma que la frecuencia de oscilación vale

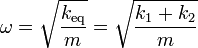
\omega = \sqrt{\frac{k_\mathrm{eq}}{m}}=\sqrt{\frac{k_1+k_2}{m}}

En particular, si las dos constantes son iguales, esto nos da una constante equivalente que es el doble de cada una de ellas.

Cuando tenemos dos muelles suspendidos en paralelo, la elongación de ambos, respecto a la posición de equilibrio, es necesariamente la misma, mientras que la fuerza es la suma de la que produce cada resorte

x = x_1 = x_2\,\qquad\qquad F= F_1+F_2

De aquí la relación entre las constantes es inmediata

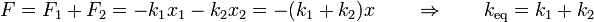
F = F_1 + F_2 = -k_1 x_1 - k_2 x_2 = -(k_1+k_2)x\qquad \Rightarrow\qquad k_\mathrm{eq}=k_1+k_2

En general, siempre que tengamos dos, tres,... resortes atados a distintos anclajes fijos (que pueden estar en diferentes puntos del espacio) y todos a la misma masa m, la constante equivalente de la asociación es igual a la suma de las constantes individuales.

4.2 Resortes en serie

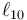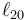Supongamos ahora dos resortes ideales de constantes k1 y k2 y longitudes en reposo \ell_{10} y \ell_{20} conectados uno a continuación del otro y una masa que cuelga del extremo inferior de la asociación. En este caso, la masa se encuentra a una distancia del techo

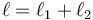
\ell = \ell_1 + \ell_2\,

Para escribir las ecuaciones de movimiento, consideraremos temporalmente que en el punto de unión de los dos muelles se encuentra una pequeña masa m0, que luego haremos tender a cero.

La segunda ley de Newton aplicada a la masa m nos da

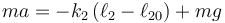
ma = -k_2\left(\ell_2-\ell_{20}\right)+mg\,

Nótese que sobre esta masa no actúa el resorte 1, ya que no se encuentra conectado a la masa y no ejerce fuerzas a distancia. Esto nos permite expresar la elongación del muelle inferior en función del peso y la aceleración de la masa

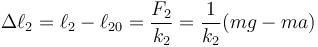
\Delta \ell_2 = \ell_2-\ell_{20} = \frac{F_2}{k_2}=\frac{1}{k_2}(mg-ma)

Sobre la masa intermedia actúan los dos resortes, cada uno tirando en un sentido, de forma que

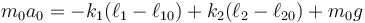
m_0a_0 = -k_1(\ell_1-\ell_{10})+k_2(\ell_2-\ell_{20})+m_0g\,

Ahora bien, si la masa intermedia es despreciable, 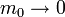m_0\to 0 y la ecuación se reduce a

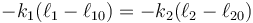
-k_1(\ell_1-\ell_{10}) = -k_2(\ell_2-\ell_{20})\,

esto es, los dos resortes ejercen la misma fuerza

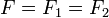
F = F_1= F_2\,

Esto nos permite calcular la elongación del muelle superior

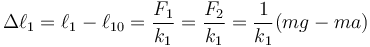
\Delta \ell_1 = \ell_1-\ell_{10} = \frac{F_1}{k_1}=\frac{F_2}{k_1}=\frac{1}{k_1}(mg-ma)

Dicho de otra forma, del muelle superior cuelga el inferior (sin masa) y la pesa que cuelga de éste. Por tanto se estira lo mismo que si colgara directamente la masa.

Sumando las dos elongaciones obtenemos la elongación total

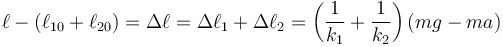
\ell-(\ell_{10}+\ell_{20}) = \Delta \ell = \Delta \ell_1 + \Delta \ell_2 = \left(\frac{1}{k_1}+\frac{1}{k_2}\right)(mg-ma)

De aquí sacamos la posición de equilibrio, que se alcanza cuando la aceleración es nula

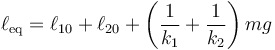
\ell_\mathrm{eq} = \ell_{10}+\ell_{20} + \left(\frac{1}{k_1}+\frac{1}{k_2}\right)mg

y definiendo la elongación respecto a la posición de equilibrio

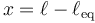
x = \ell-\ell_\mathrm{eq}\,

reducimos la ecuación de movimiento a

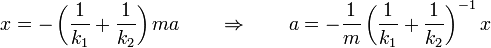
x = -\left(\frac{1}{k_1}+\frac{1}{k_2}\right)ma \qquad\Rightarrow\qquad a = -\frac{1}{m}\left(\frac{1}{k_1}+\frac{1}{k_2}\right)^{-1}x

que nos dice que la asociación se comporta como un solo resorte cuya constante verifica

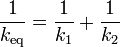
\frac{1}{k_\mathrm{eq}}=\frac{1}{k_1}+\frac{1}{k_2}

En particular, si las dos constantes son iguales, esto nos da una constante equivalente que es la mitad de cada una de ellas.

En este caso, lo que tenemos es que la elongación es la suma de las dos elongaciones, mientras que la fuerza es la misma para los dos resortes

x = x_1+x_2\qquad F=F_1=F_2

de donde resulta de manera inmediata la relación entre constantes

x = x_1+x_2 = \frac{F_1}{k_1}+\frac{F_2}{k_2}=\left(\frac{1}{k_1}+\frac{1}{k_2}\right)F\qquad\Rightarrow\qquad \frac{1}{k_\mathrm{eq}}=\frac{1}{k_1}+\frac{1}{k_2}
Obtenido de "http://tesla.us.es/wiki/index.php/Din%C3%A1mica_del_oscilador_arm%C3%B3nico_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 15:26, 30 oct 2017. - Esta página ha sido visitada 17.176 veces. - Aviso legal - Acerca de Laplace