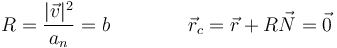Entrar Página Discusión Historial Go to the site toolbox

Masa colgando de un hilo (GIE)

De Laplace

(Diferencias entre revisiones)
 
(6 ediciones intermedias no se muestran.)
Línea 11: Línea 11:
==Posición, velocidad y aceleración==
==Posición, velocidad y aceleración==
===Posición===
===Posición===
-
La coordenada x de la partícula es inmediata
+
Tenemos que determinar la posición de la masa, que denotamos como P, de manera que
-
<center><math>x = b\cos(2\Omega t)\,</math></center>
+
<center><math>\vec{r}=\overrightarrow{OP}</math></center>
-
[[Archivo:masa-barra-polea.png|right|400px]]
+
Para determinar la posición de P lo escribimos como la suma vectorial
-
Para la coordenada y observamos que se halla a una cierta distancia por debajo de la polea P
+
<center><math>\overrightarrow{OP}=\overrightarrow{OB}+\overrightarrow{BP}</math></center>
-
<center><math>y = b\,\mathrm{sen}(2\Omega t)-(2b-c)</math></center>
+
siendo B el extremo de la barra en el cual se encuentra la polea por la que pasa el hilo. La posición de este punto B es, en el sistema de ejes indicado
-
siendo c la longitud del hilo AP. Obtenemos esta longitud observando que por tratarse de un triángulo isósceles, la altura corta a AP en su punto medio
+
<center><math>\overrightarrow{OB}=b\left(\cos(2\Omega t)\vec{\imath}+\mathrm{sen}(2\Omega t)\vec{\jmath}\right)</math></center>
 +
 
 +
Respecto a B el punto P se encuentra en la vertical por debajo
 +
 
 +
<center><math>\overrightarrow{BP}=-d\vec{\jmath}</math></center>
 +
 
 +
siendo d la longitud de hilo que cuelga. A su vez, esta longitud es igual a la total del hilo menos que la que va del extremo A a la polea de B
 +
 
 +
<center><math>d = 2b-c\qquad\qquad c = |\overrightarrow{AB}|</math></center>
 +
 
 +
Podemos obtener esta distancia c de diferentes maneras:
 +
 
 +
* A partir del teorema del coseno, puesto que conocemos los otros dos lados y el ángulo que abarcan.
 +
* Escribiendo los vectores <math>\overrightarrow{OB}</math> y <math>\overrightarrow{OA}</math> en sus componentes cartesianas y aplicando que
 +
 
 +
<center><math>\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\qquad \qquad c = |\overrightarrow{AB}|=\sqrt{\overrightarrow{AB}\cdot\overrightarrow{AB}}</math></center>
 +
 
 +
* Observando que por tratarse de un triángulo isósceles, la altura corta a AB en su punto medio
<center><math>\frac{c}{2} = b\,\mathrm{sen}(\Omega t)</math></center>
<center><math>\frac{c}{2} = b\,\mathrm{sen}(\Omega t)</math></center>
Línea 27: Línea 44:
lo que da
lo que da
-
<center><math>y = b\,\mathrm{sen}(2\Omega t)-(2b-2b\,\mathrm{sen}(\Omega t)</math></center>
+
<center><math>d = 2b-2b\,\mathrm{sen}(\Omega t)</math></center>
y para el vector de posición
y para el vector de posición
Línea 42: Línea 59:
Sustituimos el valor de t, observando que
Sustituimos el valor de t, observando que
-
<center><math>\mathrm{sen}(\Omega t)=\mathrm{sen}\left(\frac{\pi}{2}\right)=1\qquad\qquad \mathrm{sen}(2\Omega t)=\mathrm{sen}(\pi)=0\qquad\qquad \mathrm{cos}(2\Omega t)=\mathrm{sen}(\pi)=-1</math></center>
+
<center><math>\mathrm{sen}(\Omega t)=\mathrm{sen}\left(\frac{\pi}{2}\right)=1\qquad \cos(\Omega t)=\cos\left(\frac{\pi}{2}\right)=0</math></center> <br /> <center><math>\mathrm{sen}(2\Omega t)=\mathrm{sen}(\pi)=0\qquad \cos(2\Omega t)=\cos(\pi)=-1</math></center>  
y queda
y queda

última version al 11:19 20 oct 2017

Contenido

1 Enunciado

Una partícula se halla situada en el extremo de un hilo de longitud 2b, uno de cuyos extremos se encuentra en el punto A(b,0) y que pasa por una pequeña polea situada en el extremo de una barra de longitud b que gira alrededor del origen O(0,0) con velocidad angular constante 2Ω. En t = 0 la barra está completamente horizontal. La partícula cuelga verticalmente del hilo tras pasar éste por la polea y el movimiento es lo suficientemente lento como para que la partícula no oscile.

  1. Determine la posición, velocidad y aceleración de la partícula como función del tiempo.
  2. Para el instante t = π / (2Ω), halle
    1. La posición, velocidad y aceleración de la partícula.
    2. El triedro de Frenet referido a la base canónica \{\vec{\imath},\vec{\jmath},\vec{k}\}
    3. Las componentes intrínsecas de la aceleración (escalares).
    4. El radio y el centro de curvatura.

2 Posición, velocidad y aceleración

2.1 Posición

Tenemos que determinar la posición de la masa, que denotamos como P, de manera que

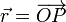
\vec{r}=\overrightarrow{OP}

Para determinar la posición de P lo escribimos como la suma vectorial

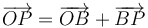
\overrightarrow{OP}=\overrightarrow{OB}+\overrightarrow{BP}

siendo B el extremo de la barra en el cual se encuentra la polea por la que pasa el hilo. La posición de este punto B es, en el sistema de ejes indicado

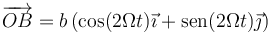
\overrightarrow{OB}=b\left(\cos(2\Omega t)\vec{\imath}+\mathrm{sen}(2\Omega t)\vec{\jmath}\right)

Respecto a B el punto P se encuentra en la vertical por debajo

\overrightarrow{BP}=-d\vec{\jmath}

siendo d la longitud de hilo que cuelga. A su vez, esta longitud es igual a la total del hilo menos que la que va del extremo A a la polea de B

d = 2b-c\qquad\qquad c = |\overrightarrow{AB}|

Podemos obtener esta distancia c de diferentes maneras:

  • A partir del teorema del coseno, puesto que conocemos los otros dos lados y el ángulo que abarcan.
  • Escribiendo los vectores 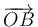\overrightarrow{OB} y \overrightarrow{OA} en sus componentes cartesianas y aplicando que
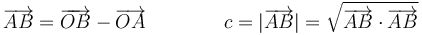
\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}\qquad \qquad c = |\overrightarrow{AB}|=\sqrt{\overrightarrow{AB}\cdot\overrightarrow{AB}}
  • Observando que por tratarse de un triángulo isósceles, la altura corta a AB en su punto medio
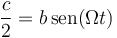
\frac{c}{2} = b\,\mathrm{sen}(\Omega t)

lo que da

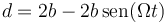
d = 2b-2b\,\mathrm{sen}(\Omega t)

y para el vector de posición

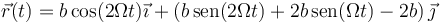
\vec{r}(t)=b\cos(2\Omega t)\vec{\imath}+\left(b\,\mathrm{sen}(2\Omega t)+2b\,\mathrm{sen}(\Omega t)-2b\right)\vec{\jmath}

2.2 Velocidad

Derivamos respecto al tiempo

\vec{v}(t)=-2b\Omega\,\mathrm{sen}(2\Omega t)\vec{\imath}+2b\Omega\left(\cos(2\Omega t)+\cos(\Omega t)\right)\vec{\jmath}

2.3 Aceleración

Volvemos a derivar respecto al tiempo

\vec{a}(t)=-4b\Omega^2\,\mathrm{cos}(2\Omega t)\vec{\imath}-2b\Omega^2\left(2\,\mathrm{sen}(2\Omega t)+\Omega\,\mathrm{sen}(\Omega t)\right)\vec{\jmath}

3 Instante t = π/2Ω

3.1 Posición, velocidad y aceleración

Sustituimos el valor de t, observando que

\mathrm{sen}(\Omega t)=\mathrm{sen}\left(\frac{\pi}{2}\right)=1\qquad \cos(\Omega t)=\cos\left(\frac{\pi}{2}\right)=0

\mathrm{sen}(2\Omega t)=\mathrm{sen}(\pi)=0\qquad \cos(2\Omega t)=\cos(\pi)=-1

y queda

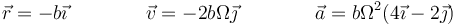
\vec{r}=-b\vec{\imath}\qquad\qquad \vec{v}=-2b\Omega\vec{\jmath}\qquad\qquad \vec{a}=b\Omega^2(4\vec{\imath}-2\vec{\jmath})

3.2 Triedro de Frenet

Para el vector tangente normalizamos la velocidad

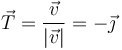
\vec{T}=\frac{\vec{v}}{|\vec{v}|}=-\vec{\jmath}

El binormal es el perpendicular al plano del movimiento

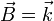
\vec{B}=\vec{k}

El normal es el producto de los dos anteriores

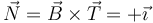
\vec{N}=\vec{B}\times\vec{T}=+\vec{\imath}

3.3 Componentes intrínsecas

La aceleración tangencial es la proyección de la aceleración sobre el vector tangente

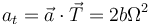
a_t=\vec{a}\cdot\vec{T}=2b\Omega^2

La normal es la proyección sobre el vector normal

a_n =\vec{a}\cdot\vec{N} = 4b\Omega^2

3.4 Radio y centro de curvatura

A partir de la rapidez y la aceleración normal

R=\frac{|\vec{v}|^2}{a_n}=b\qquad\qquad \vec{r}_c=\vec{r}+R\vec{N}=\vec{0}
Obtenido de "http://tesla.us.es/wiki/index.php/Masa_colgando_de_un_hilo_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 11:19, 20 oct 2017. - Esta página ha sido visitada 1.884 veces. - Aviso legal - Acerca de Laplace