Entrar Página Discusión Historial Go to the site toolbox

Test del tercer parcial 2016-2017 (GIE)

De Laplace

(Diferencias entre revisiones)
 
(7 ediciones intermedias no se muestran.)
Línea 4: Línea 4:
===Pregunta 1===
===Pregunta 1===
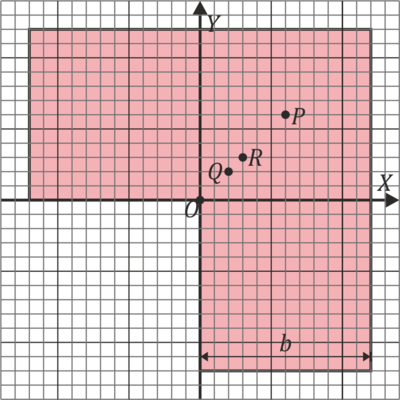
¿Dónde se halla el centro de masas de la pieza?
¿Dónde se halla el centro de masas de la pieza?
-
:* '''A''' En O(0,0).
+
:* '''A''' En <math>O(0,0)\,</math>.
-
:* '''B''' En P(b\/2,b\/2).
+
:* '''B''' En <math>P(b/2,b/2)\,</math>.
-
:* '''C''' En Q(b/6,b/6).
+
:* '''C''' En <math>Q(b/6,b/6)\,</math>.
-
:* '''D''' En R(b\/4,b\/4).
+
:* '''D''' En <math>R(b/4,b/4)\,</math>.
;Solucin:
;Solucin:
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
===Pregunta 2===
===Pregunta 2===
-
Si el momento de inercia de una placa cuadrada de lado <math>b</math> y masa <math>m_0</math> respecto a un eje perpendicular a ella por su centro vale <math>I_0=m_0 b^2/6</math>, ´¿cuánto vale el momento de inercia de esta figura respecto a un eje perpendicular a ella y que pasa por O?
+
Si el momento de inercia de una placa cuadrada de lado <math>b</math> y masa <math>m_0</math> respecto a un eje perpendicular a ella por su centro vale <math>I_0=m_0 b^2/6\,</math>, ¿cuánto vale el momento de inercia de esta figura respecto a un eje perpendicular a ella y que pasa por O?
-
:* '''A''' <math>I=2mb^2/3</math>.
+
:* '''A''' <math>I=2mb^2/3\,</math>.
-
:* '''B''' <math>I=mb^2/6</math>.
+
:* '''B''' <math>I=mb^2/6\,</math>.
-
:* '''C''' <math>I=mb^2/2</math>.
+
:* '''C''' <math>I=mb^2/2\,</math>.
-
:* '''D''' <math>I=2mb^2</math>.
+
:* '''D''' <math>I=2mb^2\,</math>.
;Solución:
;Solución:
La respuesta correcta es la '''<span style="color:red;">A<span>'''.
La respuesta correcta es la '''<span style="color:red;">A<span>'''.
 +
 +
==Ley de conservación==
 +
Un sólido rígido se mueve por el aire sometido exclusivamente a la acción de los pesos de sus partículas (el rozamiento con el aire es despreciable). Si <math>\vec{g}⃗=-g\vec{\jmath}</math>, ¿cuál de las siguientes propiedades del sólido ''no'' se conserva en su movimiento?
 +
:* '''A''' El momento cinético respecto a un punto fijo O.
 +
:* '''B''' La componente X de su cantidad de movimiento.
 +
:* '''C''' La energía mecánica.
 +
:* '''D''' El momento cinético respecto al centro de masas del sólido.
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">A<span>'''.
 +
 +
==Sistema de fuerzas==
 +
[[Archivo:dos-fuerzas-solido.png|right|400px]]
 +
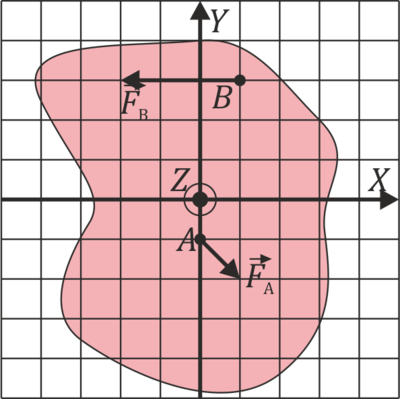
Sobre un sólido rígido situado en el plano OXY actúan las dos fuerzas indicadas en la figura (la rejilla representa m para distancias y N para fuerzas)
 +
 +
===Pregunta 1===
 +
¿A qué equivale este sistema de fuerzas?
 +
:* '''A''' Par de fuerzas.
 +
:* '''B''' Sistema nulo.
 +
:* '''C''' Fuerza única.
 +
:* '''D''' Tornillo.
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">C<span>'''.
 +
 +
===Pregunta 2===
 +
¿Dónde habría que aplicar una fuerza y cuánto debería valer ésta en newtons para que el sistema quedara en equilibrio?
 +
:* '''A''' En C(1,0) y de valor <math>\vec{F}_C=2\vec{\imath}+\vec{\jmath}</math>.
 +
:* '''B''' En C(1,0) y de valor <math>\vec{F}_C=\vec{k}</math>.
 +
:* '''C''' Es imposible anular este sistema con una tercera fuerza.
 +
:* '''D''' En D(&minus;4,3) y de valor <math>\vec{F}_D=2\vec{\imath}+\vec{\jmath}</math>.
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">D<span>'''.
 +
 +
==Movimiento de un sólido==
 +
En un movimiento de un sólido rígido, el eje instantáneo de rotación (y mínimo deslizamiento, en su caso) pasa por los puntos O(0,0,0) y A(2,1,&minus;2) (en m). En el mismo instante, la velocidad del punto B(1,2,2) es, en m/s, <math>\vec{v}_B=10\vec{\imath}-13\vec{\jmath}+8\vec{k}</math>.
 +
===Pregunta 1===
 +
¿Qué tipo de movimiento está describiendo el sólido en dicho instante?
 +
:* '''A''' Traslación.
 +
:* '''B''' Espiral.
 +
:* '''C''' Rotación.
 +
:* '''D''' Helicoidal.
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">D<span>'''.
 +
 +
===Pregunta 2===
 +
¿Cuánto vale la velocidad de deslizamiento del sólido, en m/s?
 +
:* '''A''' <math>\sqrt{333}</math>.
 +
:* '''B''' &minus;3.
 +
:* '''C''' +1.
 +
:* '''D''' 0.
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">B<span>'''.
 +
===Pregunta 3===
 +
¿Cuánto vale el vector velocidad angular del sólido, en rad/s?
 +
:* '''A''' <math>-2\vec{\imath}-\vec{\jmath}+2\vec{k}</math>.
 +
:* '''B''' <math>4\vec{\imath}+2\vec{\jmath}-4\vec{k}</math>.
 +
:* '''C''' No hay suficiente información para determinarla.
 +
:* '''D''' <math>-2\vec{\imath}+2\vec{\jmath}-k\vec{k}</math>.
 +
;Solución:
 +
La respuesta correcta es la '''<span style="color:red;">B<span>'''.
 +
[[Categoría:preguntas de test de Física I (GIE)]]

última version al 17:40 23 ene 2017

Contenido

1 Placa en forma de L

Se tiene una chapa metálica de pequeño espesor con densidad superficial uniforme, siendo la masa total m, en forma de L construida a partir de un cuadrado de lado 2b en el que se ha recortado una esquina cuadrada de lado b.

1.1 Pregunta 1

¿Dónde se halla el centro de masas de la pieza?

  • A En O(0,0)\,.
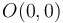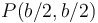  • B En P(b/2,b/2)\,.
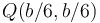  • C En Q(b/6,b/6)\,.
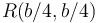  • D En R(b/4,b/4)\,.
Solucin

La respuesta correcta es la C.

1.2 Pregunta 2

Si el momento de inercia de una placa cuadrada de lado b y masa m0 respecto a un eje perpendicular a ella por su centro vale 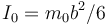I_0=m_0 b^2/6\,, ¿cuánto vale el momento de inercia de esta figura respecto a un eje perpendicular a ella y que pasa por O?

  • A 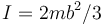I=2mb^2/3\,.
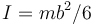  • B I=mb^2/6\,.
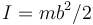  • C I=mb^2/2\,.
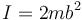  • D I=2mb^2\,.
Solución

La respuesta correcta es la A.

2 Ley de conservación

Un sólido rígido se mueve por el aire sometido exclusivamente a la acción de los pesos de sus partículas (el rozamiento con el aire es despreciable). Si 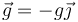\vec{g}⃗=-g\vec{\jmath}, ¿cuál de las siguientes propiedades del sólido no se conserva en su movimiento?

  • A El momento cinético respecto a un punto fijo O.
  • B La componente X de su cantidad de movimiento.
  • C La energía mecánica.
  • D El momento cinético respecto al centro de masas del sólido.
Solución

La respuesta correcta es la A.

3 Sistema de fuerzas

Sobre un sólido rígido situado en el plano OXY actúan las dos fuerzas indicadas en la figura (la rejilla representa m para distancias y N para fuerzas)

3.1 Pregunta 1

¿A qué equivale este sistema de fuerzas?

  • A Par de fuerzas.
  • B Sistema nulo.
  • C Fuerza única.
  • D Tornillo.
Solución

La respuesta correcta es la C.

3.2 Pregunta 2

¿Dónde habría que aplicar una fuerza y cuánto debería valer ésta en newtons para que el sistema quedara en equilibrio?

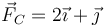  • A En C(1,0) y de valor \vec{F}_C=2\vec{\imath}+\vec{\jmath}.
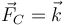  • B En C(1,0) y de valor \vec{F}_C=\vec{k}.
  • C Es imposible anular este sistema con una tercera fuerza.
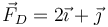  • D En D(−4,3) y de valor \vec{F}_D=2\vec{\imath}+\vec{\jmath}.
Solución

La respuesta correcta es la D.

4 Movimiento de un sólido

En un movimiento de un sólido rígido, el eje instantáneo de rotación (y mínimo deslizamiento, en su caso) pasa por los puntos O(0,0,0) y A(2,1,−2) (en m). En el mismo instante, la velocidad del punto B(1,2,2) es, en m/s, 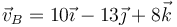\vec{v}_B=10\vec{\imath}-13\vec{\jmath}+8\vec{k}.

4.1 Pregunta 1

¿Qué tipo de movimiento está describiendo el sólido en dicho instante?

  • A Traslación.
  • B Espiral.
  • C Rotación.
  • D Helicoidal.
Solución

La respuesta correcta es la D.

4.2 Pregunta 2

¿Cuánto vale la velocidad de deslizamiento del sólido, en m/s?

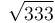  • A \sqrt{333}.
  • B −3.
  • C +1.
  • D 0.
Solución

La respuesta correcta es la B.

4.3 Pregunta 3

¿Cuánto vale el vector velocidad angular del sólido, en rad/s?

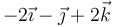  • A -2\vec{\imath}-\vec{\jmath}+2\vec{k}.
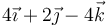  • B 4\vec{\imath}+2\vec{\jmath}-4\vec{k}.
  • C No hay suficiente información para determinarla.
  • D 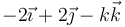-2\vec{\imath}+2\vec{\jmath}-k\vec{k}.
Solución

La respuesta correcta es la B.

Obtenido de "http://tesla.us.es/wiki/index.php/Test_del_tercer_parcial_2016-2017_(GIE)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 17:40, 23 ene 2017. - Esta página ha sido visitada 1.825 veces. - Aviso legal - Acerca de Laplace