Dos discos articulados en un eje
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Dos discos delgados, ambos de masa <math>m</math> y radio <math>r</math>, están conectados por un eje delgado de masa <math>m_0</math> y longitud <math>b</math>. …') |
(→Resultados) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 5: | Línea 5: | ||
# Suponga que, estando en reposo el sistema con el eje alineado con el OX y el punto de contacto de uno de los discos situado en el origen se aplica una percusión <math>\vec{P}</math> horizontal y perpendicular a la barra a una distancia <math>c</math> de su centro. Determine el movimiento del sistema a partir de ese momento | # Suponga que, estando en reposo el sistema con el eje alineado con el OX y el punto de contacto de uno de los discos situado en el origen se aplica una percusión <math>\vec{P}</math> horizontal y perpendicular a la barra a una distancia <math>c</math> de su centro. Determine el movimiento del sistema a partir de ese momento | ||
| - | <center>[[Archivo:dos-discos-eje.png]]</center> | + | <center>[[Archivo:dos-discos-eje.png|500px]]</center> |
==Resultados== | ==Resultados== | ||
| Línea 19: | Línea 19: | ||
;Momento cinético respecto al CM | ;Momento cinético respecto al CM | ||
| - | <center><math>\vec{L}_G=(-mrv_G)\vec{\imath}_0+\frac{m_0b^2+ | + | <center><math>\vec{L}_G=(-mrv_G)\vec{\imath}_0+\left(\frac{m_0b^2}{12}+\frac{m(b^2+r^2)}{2}\right)\dot{\theta}\vec{k}_0</math></center> |
;Energía cinética: | ;Energía cinética: | ||
| Línea 26: | Línea 26: | ||
;Velocidad del CM tras la percusión | ;Velocidad del CM tras la percusión | ||
| + | |||
| + | <center><math>\vec{v}^G_{01}=v_G\vec{\jmath}_0=\frac{P}{m_0+3m}\vec{\jmath}_0</math></center> | ||
| + | |||
| + | ;Velocidad angular del eje tras la percusión | ||
| + | |||
| + | <center><math>\dot{\theta}=\frac{12 c P}{m_0 b^2+ m(9 b^2+6r^2)}</math></center> | ||
| + | |||
| + | Tras la percusión, ambas cantidades permanecen constantes. | ||
última version al 14:18 27 nov 2016
1 Enunciado
Dos discos delgados, ambos de masa m y radio r, están conectados por un eje delgado de masa m0 y longitud b. Los discos pueden rodar sin deslizar por el plano OXY. El eje está articulado en dos rodamientos, de forma que las dos ruedas pueden girar libremente en torno a él.
- Determine la energía cinética del sistema en función de la velocidad del CM del conjunto y de la velocidad angular
con la que gira la barra en torno a un eje vertical.
- Suponga que, estando en reposo el sistema con el eje alineado con el OX y el punto de contacto de uno de los discos situado en el origen se aplica una percusión
horizontal y perpendicular a la barra a una distancia c de su centro. Determine el movimiento del sistema a partir de ese momento
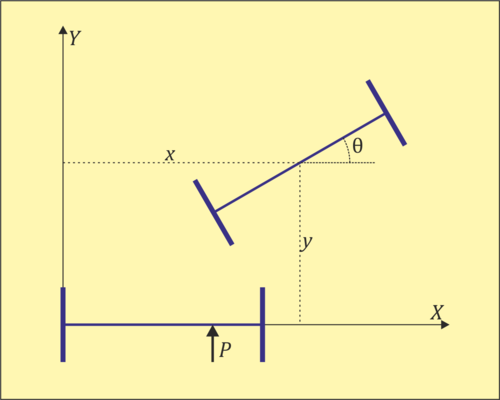
2 Resultados
- Cantidad de movimiento
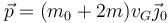
Siendo la base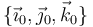 
una ligada al eje, con el OX0 a lo largo de él, y el OZ0 perpendicular al plano de movimiento.
vG se relaciona con las coordenadas como
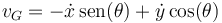
- Momento cinético respecto al CM
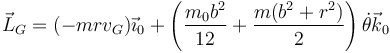
- Energía cinética
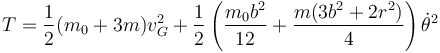
- Velocidad del CM tras la percusión
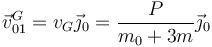
- Velocidad angular del eje tras la percusión
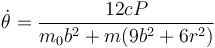
Tras la percusión, ambas cantidades permanecen constantes.
