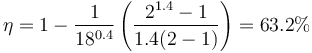Caso práctico de ciclo Diesel (GIE)
De Laplace
| (4 ediciones intermedias no se muestran.) | |||
| Línea 66: | Línea 66: | ||
| 290 | | 290 | ||
| 1800 | | 1800 | ||
| + | |- | ||
| + | ! B | ||
| + | | 8.58 | ||
| + | | 922 | ||
| + | | 100 | ||
| + | |} | ||
| + | |||
| + | ===Estado C (tras la combustión)=== | ||
| + | En el ciclo Diesel ideal la combustión se realiza a presión constante, por lo que | ||
| + | |||
| + | <center><math>p_C=p_B = 8.58\,\mathrm{MPa}</math></center> | ||
| + | |||
| + | Nos dan como dato la relación de combustión, lo que nos proporciona el volumen | ||
| + | |||
| + | <center><math>\frac{v_C}{V_B}=r_c = 2\qquad\Rightarrow\qquad V_C = 200\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | y la temperatura, por la ley de Charles | ||
| + | |||
| + | <center><math>(p_B=p_C)\qquad\qquad \frac{V_C}{T_C}=\frac{V_B}{T_B}\qquad\Rightarrow\qquad T_C=T_B r_c = 1843\,\mathrm{K}</math></center> | ||
| + | |||
| + | Añadimos la línea | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Estado | ||
| + | ! p (MPa) | ||
| + | ! T (K) | ||
| + | ! V (cm³) | ||
|- | |- | ||
! A | ! A | ||
| + | | 0.15 | ||
| + | | 290 | ||
| + | | 1800 | ||
| + | |- | ||
| + | ! B | ||
| 8.58 | | 8.58 | ||
| 922 | | 922 | ||
| 100 | | 100 | ||
| + | |- | ||
| + | ! C | ||
| + | | 8.58 | ||
| + | | 1843 | ||
| + | | 200 | ||
|} | |} | ||
| - | === | + | ===Estado D (tras la expansión)=== |
| + | En el ciclo Diesel ideal se supone que el volumen tras la expansión es el mismo que antes de la compresión | ||
| + | |||
| + | <center><math>V_D=V_A=1800\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | La presión la calculamos de nuevo por la ley de Poisson, ya que suponemos que la expansión es adiabática | ||
| + | |||
| + | <center><math>p_D = p_C\left(\frac{V_C}{V_D}\right)^\gamma</math></center> | ||
| + | |||
| + | lo que da | ||
| + | |||
| + | <center><math>p_D=0.396\,\mathrm{MPa}</math></center> | ||
| + | |||
| + | y la temperatura | ||
| + | |||
| + | <center><math>T_D = T_C\left(\frac{V_C}{V_D}\right)^{\gamma-1}=765\,\mathrm{K}</math></center> | ||
| + | |||
| + | lo que nos permite completar la tabla | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Estado | ||
| + | ! p (MPa) | ||
| + | ! T (K) | ||
| + | ! V (cm³) | ||
| + | |- | ||
| + | ! A | ||
| + | | 0.15 | ||
| + | | 290 | ||
| + | | 1800 | ||
| + | |- | ||
| + | ! B | ||
| + | | 8.58 | ||
| + | | 922 | ||
| + | | 100 | ||
| + | |- | ||
| + | ! C | ||
| + | | 8.58 | ||
| + | | 1843 | ||
| + | | 200 | ||
| + | |- | ||
| + | ! A | ||
| + | | 0.40 | ||
| + | | 765 | ||
| + | | 1800 | ||
| + | |} | ||
| + | |||
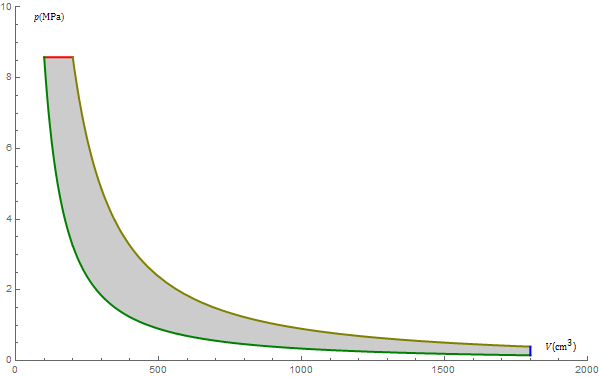
| + | <center>[[Archivo:diesel-real.png]]</center> | ||
| + | |||
==Calor y trabajo== | ==Calor y trabajo== | ||
| + | ===Calor absorbido=== | ||
| + | El calor se absorbe durante la combustión, que modelamos como un proceso a presión constante | ||
| + | |||
| + | <center><math>Q_\mathrm{in}=\Delta H = nc_p(T_C-T_B)</math></center> | ||
| + | |||
| + | Aplicando la relación | ||
| + | |||
| + | <center><math>c_p=\frac{\gamma R}{\gamma-1}</math></center> | ||
| + | |||
| + | queda | ||
| + | |||
| + | <center><math>Q_\mathrm{in} = \frac{\gamma p_B(V_C-V_B)}{\gamma-1}</math></center> | ||
| + | |||
| + | con el valor numérico | ||
| + | |||
| + | <center><math>Q_\mathrm{in}=\frac{1.4\times 8.58\,\mathrm{MPa}(200-100)\mathrm{cm}^3}{0.4}=3.00\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | ===Calor cedido=== | ||
| + | El calor se cede a volumen constante | ||
| + | |||
| + | <center><math>Q_\mathrm{out}=|\Delta U| = nc_v(T_D-T_A)</math></center> | ||
| + | |||
| + | Aplicando la relación | ||
| + | |||
| + | <center><math>c_v=\frac{R}{\gamma-1}</math></center> | ||
| + | |||
| + | queda | ||
| + | |||
| + | <center><math>Q_\mathrm{out} = \frac{(p_D-p_A)V_A}{\gamma-1}</math></center> | ||
| + | |||
| + | con el valor numérico | ||
| + | |||
| + | <center><math>Q_\mathrm{out}=\frac{ (0.40-0.15)\,\mathrm{MPa}\times 1800\mathrm{cm}^3}{0.4}=1.11\,\mathrm{kJ}</math></center> | ||
| + | |||
| + | ===Trabajo neto realizado=== | ||
| + | El trabajo neto que realiza el ciclo lo obtenemos como la diferencia entre el calor absorbido y el cedido | ||
| + | |||
| + | <center><math>W_\mathrm{out,neto}=Q_\mathrm{in}-Q_\mathrm{out}=1.90\,\mathrm{kJ}</math></center> | ||
| + | |||
==Rendimiento== | ==Rendimiento== | ||
| + | El rendimiento es el cocidente entre el trabajo realizado y el calor absorbido | ||
| + | |||
| + | <center><math>\eta=\frac{W_\mathrm{out,neto}}{Q_\mathrm{in}}= 63.2\%</math></center> | ||
| + | |||
| + | También puede calcularse directamente a partir de la relación de compresión y de combustión | ||
| + | |||
| + | <center><math>\eta = 1-\frac{1}{r^{\gamma-1}}\left(\frac{r_c^\gamma-1}{\gamma(r_c-1)}\right)</math></center> | ||
| + | |||
| + | y queda | ||
| + | |||
| + | <center><math>\eta = 1 -\frac{1}{18^{0.4}}\left(\frac{2^{1.4}-1}{1.4(2-1)}\right)=63.2\%</math></center> | ||
| + | |||
| + | |||
[[Categoría:Problemas de máquinas térmicas (GIE)]] | [[Categoría:Problemas de máquinas térmicas (GIE)]] | ||
última version al 13:39 28 may 2016
Contenido |
1 Enunciado
Suponga un motor diésel turbo con una cilindrada de 1700 cm³. En este motor el aire a la entrada está a una presión de 150 kPa y una temperatura de 17 °C. Si para este motor la razón de compresión es 18 y la de combustión vale 2, determine los volúmenes, presiones y temperaturas de cada vértice del ciclo, así como su rendimiento y el calor y el trabajo intercambiados por el motor.
2 Presiones, volúmenes y temperaturas
2.1 Estado A (antes de la compresión)
El volumen inicial y tras la compresión los obtenemos de que conocemos la cilindrada y la relación de compresión
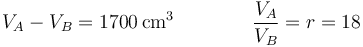
lo que nos da

La presión y la temperatura antes de la compresión son datos del problema

Construimos una tabla con estos valores, que iremos ampliando más tarde
| Estado | p (MPa) | T (K) | V (cm³) |
|---|---|---|---|
| A | 0.150 | 290 | 1800 |
2.2 Estado B (tras la compresión)
Si, como aproximación, suponemos que el proceso es adiabático y cuasiestático, podemos emplear la fórmula de Poisson
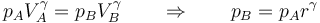
lo que da
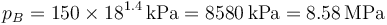
La temperatura la podemos calcular empleando la ley de Poisson

o la de los gases ideales
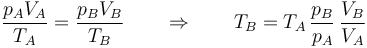
y resulta
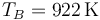
Añadimos la fila a la tabla
| Estado | p (MPa) | T (K) | V (cm³) |
|---|---|---|---|
| A | 0.15 | 290 | 1800 |
| B | 8.58 | 922 | 100 |
2.3 Estado C (tras la combustión)
En el ciclo Diesel ideal la combustión se realiza a presión constante, por lo que
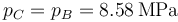
Nos dan como dato la relación de combustión, lo que nos proporciona el volumen

y la temperatura, por la ley de Charles
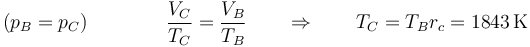
Añadimos la línea
| Estado | p (MPa) | T (K) | V (cm³) |
|---|---|---|---|
| A | 0.15 | 290 | 1800 |
| B | 8.58 | 922 | 100 |
| C | 8.58 | 1843 | 200 |
2.4 Estado D (tras la expansión)
En el ciclo Diesel ideal se supone que el volumen tras la expansión es el mismo que antes de la compresión
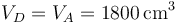
La presión la calculamos de nuevo por la ley de Poisson, ya que suponemos que la expansión es adiabática
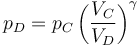
lo que da
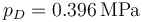
y la temperatura
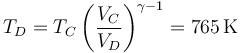
lo que nos permite completar la tabla
| Estado | p (MPa) | T (K) | V (cm³) |
|---|---|---|---|
| A | 0.15 | 290 | 1800 |
| B | 8.58 | 922 | 100 |
| C | 8.58 | 1843 | 200 |
| A | 0.40 | 765 | 1800 |
3 Calor y trabajo
3.1 Calor absorbido
El calor se absorbe durante la combustión, que modelamos como un proceso a presión constante
Aplicando la relación
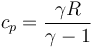
queda
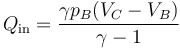
con el valor numérico
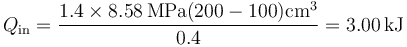
3.2 Calor cedido
El calor se cede a volumen constante
Aplicando la relación
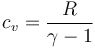
queda
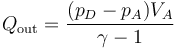
con el valor numérico

3.3 Trabajo neto realizado
El trabajo neto que realiza el ciclo lo obtenemos como la diferencia entre el calor absorbido y el cedido
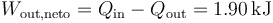
4 Rendimiento
El rendimiento es el cocidente entre el trabajo realizado y el calor absorbido
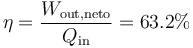
También puede calcularse directamente a partir de la relación de compresión y de combustión
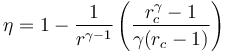
y queda