Prueba
De Laplace
(Diferencias entre revisiones)
(→Otra sección) |
(→Discos) |
||
| (13 ediciones intermedias no se muestran.) | |||
| Línea 15: | Línea 15: | ||
====Ejemplo de sección==== | ====Ejemplo de sección==== | ||
Texto de la sección | Texto de la sección | ||
| - | ===== | + | ==Discos== |
| + | <center><math>\vec{p}=(m_0+2m)v_G\vec{\jmath}_0</math></center> | ||
| - | <center><math> | + | <center><math>\vec{L}_G=(-mrv_G)\vec{\imath}_0+\frac{m_0b^2+6m(b^2+r^2)}{12}\dot{\theta}\vec{k}_0</math></center> |
| + | <center><math>T=\frac{1}{2}(m_0+3m)v_G^2 +\frac{1}{2}\left(\frac{m_0b^2}{12}+\frac{m(3b^2+2r^2)}{4}\right)\dot{\theta}^2</math></center> | ||
| - | + | siendo | |
| - | < | + | <center><math>v_G=-\dot{x}\,\mathrm{sen}(\theta)+\dot{y}\cos(\theta)</math></center> |
| - | < | + | <center><math>\mathcal{L}=\mathcal{L}(q_i,\dot{q}_i)\qquad\qquad \frac{\partial \mathcal{L}}{\partial t}=0</math></center> |
| - | < | + | <center><math>h=\sum_i \dot{q}_i\frac{\partial \mathcal{L}}{\partial \dot{q}_i}-\mathcal{L}</math></center> |
| - | + | == Otra sección== | |
| - | |||
| - | |||
| - | < | + | <math>\overrightarrow{OP}=\frac{\vec{R}\times \vec{M}_O}{|\vec{R}|^2}+\lambda \vec{R}</math> |
| - | < | + | <math>\vec{v}=\vec{v}_0+\vec{a}t</math> |
| - | < | + | <math>\vec{r}=\vec{r}_0+\vec{v}_0t+\frac{1}{2}\vec{a}t^2</math> |
| - | < | + | <math>\vec{r}(t=0)=\vec{r}_0=4\vec{\imath}+3\vec{\jmath}</math> |
| - | < | + | <math>\vec{r}(t=2)=\vec{r}_1=10\vec{\imath}-2\vec{\jmath}</math> |
| - | < | + | <math>10\vec{\imath}-2\vec{\jmath}=4\vec{\imath}+3\vec{\jmath}+2\vec{v}_0+2\vec{a}</math> |
| - | < | + | <math> |
| + | \vec{v}(t=2) = 5\vec{\imath}-6\vec{\jmath}</math> | ||
| - | < | + | <math> 5\vec{\imath}-6\vec{\jmath} = \vec{v}_0+2\vec{a}</math> |
| + | <math> | ||
| + | 2\vec{v}_0+2\vec{a}=6\vec{\imath}-5\vec{\jmath} | ||
| + | </math> | ||
| + | <math>\vec{v}_0+2\vec{a}= 5\vec{\imath}-6\vec{\jmath}</math> | ||
| + | <math>\vec{v}_0=\vec{\imath}+\vec{\jmath}</math> | ||
| - | + | <math>\vec{a}=2\vec{\imath}-\frac{7}{2}\vec{\jmath}</math> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
[[Archivo:energia-multiple.gif]] | [[Archivo:energia-multiple.gif]] | ||
última version al 17:43 4 ene 2016
Contenido |
1 Ejemplo de sección
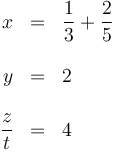
1.1 Ejemplo de subsección
Texto de la sección
1.2 Otra subsección
Texto de la sección
1.2.1 Ejemplo de sección
Texto de la sección
2 Discos
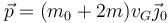
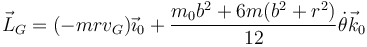
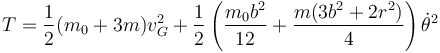
siendo
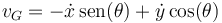

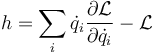
3 Otra sección

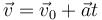

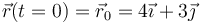

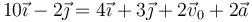

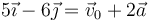
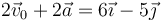
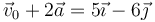


Ejemplo de lista con apartados
- Un apartado
- Otro
- Otro más
- Un subapartado
- Otro
- Un subapartado
- Un apartado
Ejemplo de lista numerada
- Un apartado
- Otro
- Otro más
- Un subapartado
- Otro
- Un subapartado
- Un apartado
Descripción:
- Ataúlfo
- El primero
- Sigerico
- El segundo
- Walia
- Otro más
Un poco de todo
Algunas ecuaciones
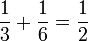
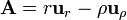
Una imagen

Una miniatura
Algunos enlaces
Enlace interno: Segundo Principio
Enlace externo: Página de campos







