Fórmulas posiblemente con dimensiones incorrectas
De Laplace
(→Enunciado) |
(→Enunciado) |
||
| (15 ediciones intermedias no se muestran.) | |||
| Línea 2: | Línea 2: | ||
Teniendo en cuenta las dimensiones calculadas en el problema [[Ejemplos_de_cálculo_de_dimensiones|anterior]], indique cuáles de las siguientes expresiones son necesariamente incorrectas: | Teniendo en cuenta las dimensiones calculadas en el problema [[Ejemplos_de_cálculo_de_dimensiones|anterior]], indique cuáles de las siguientes expresiones son necesariamente incorrectas: | ||
| - | :a) <math>W = \frac{1}{2}mv^2 + gy</math> | + | : a) <math>\displaystyle W = \frac{1}{2}mv^2 + gy</math> |
| - | :b) <math>\ | + | : b) <math>\displaystyle v=\frac{x-1}{t-2}</math> |
| - | :c) <math>\ | + | : c) <math>\displaystyle P = m\frac{(v^2/R - a)}{(t-x/v)}(x-\pi R^2)</math> |
| - | :d) <math>\ | + | : d) <math>\displaystyle \int_0^T \vec{F}\,\mathrm{d}t = \frac{\mathrm{d}m}{\mathrm{d}t}\vec{v}+ m\vec{a}t</math> |
| - | :e) <math>\ | + | : e)<math>\displaystyle \int_{t_1}^{t_2}\frac{P-\vec{v}\cdot(\vec{a}+\vec{p}/m)}{v^2}\,\mathrm{d}t = \frac{m(t-2/t)}{v}</math> |
| - | :f) <math>\int_0^T (P-\vec{F}\cdot\vec{v})\,\mathrm{d}t = mgh + \frac{p^2}{2m}</math> | + | : f) <math>\displaystyle \int_0^T (P-\vec{F}\cdot\vec{v})\,\mathrm{d}t = mgh + \frac{p^2}{2m}</math> |
| - | :g) <math> | + | : g) <math>\vec{r}\times\vec{L} = R^2\vec{p}</math> |
| - | :h) <math>\ | + | : h) <math>\displaystyle \vec{M} = \vec{r}\times\vec{F}+\vec{v}\times\vec{p}</math> |
==Caso (a)== | ==Caso (a)== | ||
| Línea 25: | Línea 25: | ||
<center><math>W = \frac{1}{2}mv^2 + gy</math></center> | <center><math>W = \frac{1}{2}mv^2 + gy</math></center> | ||
| - | tenemos que el [[Ejemplos_de_análisis_dimensional#Trabajo| | + | tenemos que el [[Ejemplos_de_análisis_dimensional#Trabajo|trabajo]] tiene dimensiones de masa por velocidad al cuadrado |
<center><math>[W]= M L^2T^{-2}\,</math></center> | <center><math>[W]= M L^2T^{-2}\,</math></center> | ||
| Línea 40: | Línea 40: | ||
==Caso (b)== | ==Caso (b)== | ||
| - | + | La formula | |
| - | <center><math>\ | + | <center><math>\displaystyle v=\frac{x-1}{t-2}</math></center> |
| - | + | podría parecer correcta a primera vista. Después de todo, la velocidad tiene dimensiones de distancia dividida por tiempo. Sin embargo no es correcta. La razón está en ese “1” y ese “2” del numerador y el denominador. Si no se dice otra cosa, un número, como el 2, es una cantidad adimensional. Por tanto en el denominador estamos restando una cantidad adimensional a una que sí tiene dimensiones (tiempo), lo que viola el principio de homogeneidad. | |
| - | + | Para que una fórmula de este tipo (de las que aparecen a menudo en problemas de libros de texto) sea correcta, debe especificarse previamente que se sobreentiende que todas las unidades están en el SI, de forma que el 1 del numerador quiere decir en realidad "1\thinsp;m" y el 2 del denominador es en realidad “2\thinsp;s”. | |
| - | y el | + | Si no se hace así, o se usan unidades que no son del SI, es muy posible que los cálculos de un problema conduzcan a error. Por ejemplo, si se dice que la densidad del agua es “1”, y nada más, y se sustituye así en las fórmulas, casi seguro van a obtenerse resultados incorrectos, ya que realmente es “1\thinso;g/cm³” (o, en el SI 1000\thinsp;kg/m³) |
| - | |||
| - | |||
| - | |||
==Caso (c)== | ==Caso (c)== | ||
| - | En | + | En la expresión |
| - | <center><math> | + | <center><math>P = m\frac{(v^2/R - a)}{(t-x/v)}(x-\pi R^2)</math></center> |
| - | + | aparecen muchos factores que habría que analizar por separado. Sin embargo, es fácil ver que esta fórmula es incorrecta. En el último factor tenemos la combinación | |
| - | <center><math> | + | <center><math>(x-\pi R^2)\,</math></center> |
| - | + | en la cual se suma una longitud (de dimensión <math>L</math>) con un área (de dimensión <math>L^2</math>), lo cual es incorrecto y por ello toda la fórmula está mal. | |
| - | |||
| - | + | ==Caso (d)== | |
| + | En la fórmula | ||
| - | <center><math>\ | + | <center><math>\int_0^T \vec{F}\,\mathrm{d}t = \frac{\mathrm{d}m}{\mathrm{d}t}\vec{v}+ m\vec{a}t</math></center> |
| - | + | aparece una integral, que no es más que una suma de muchas cantidades muy pequeñas. Como toda suma, los sumandos deben ser dimensionalmente equivalentes y el resultado tiene las mismas dimensiones que cualquiera de ellos. En este caso | |
| - | ==Caso (d)== | + | <center><math>\left[\int_0^T \vec{F}\,\mathrm{d}t\right] = [F][t]=MLT^{-1}</math></center> |
| + | |||
| + | En el segundo miembro tenemos, para el primer sumando | ||
| + | |||
| + | <center><math>\left[\frac{\mathrm{d}m}{\mathrm{d}t}\right] = \frac{[m]}{[t]}[v] = \frac{M}{T}LT^{-1} = M LT^{-2}</math></center> | ||
| + | |||
| + | Estas dimensiones no coinciden con las del primer miembro, por lo que ya no hace falta seguir. Esta fórmula es necesariamente incorrecta. | ||
| + | |||
| + | ==Caso (e)== | ||
| + | Para la fórmula | ||
| + | |||
| + | <center><math>\int_{t_1}^{t_2}\frac{P-\vec{v}\cdot(\vec{a}+\vec{p}/m)}{v^2}\,\mathrm{d}t = \frac{m(t-2/t)}{v}</math></center> | ||
| + | |||
| + | el razonamiento es idéntico al del caso (c). En el numerador del segundo miembro se resta de un tiempo (de dimensión <math>T</math>) la inversa de un tiempo (de dimensión <math>T^{-1}</math>) lo cual no es admisible y no hace falta seguir. | ||
| + | |||
| + | <!-- | ||
| + | ==Caso (e)== | ||
En el caso | En el caso | ||
| Línea 99: | Línea 112: | ||
Dado que estas dimensiones (de una velocidad) son las mismas que habíamos obtenido para el miembro, esta ecuación es dimensionalmente correcta. | Dado que estas dimensiones (de una velocidad) son las mismas que habíamos obtenido para el miembro, esta ecuación es dimensionalmente correcta. | ||
| - | + | --> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
==Caso (f)== | ==Caso (f)== | ||
Para la fórmula | Para la fórmula | ||
| - | <center><math>\ | + | <center><math>\int_0^T (P-\vec{F}\cdot\vec{v})\,\mathrm{d}t = mgh + \frac{p^2}{2m}</math></center> |
Analizamos en primer lugar el paréntesis del integrando | Analizamos en primer lugar el paréntesis del integrando | ||
| Línea 126: | Línea 125: | ||
por lo que la suma es dimensionalmente correcta. Las dimensiones de la integral son | por lo que la suma es dimensionalmente correcta. Las dimensiones de la integral son | ||
| - | <center><math>\left[\ | + | <center><math>\left[\int_0^T (P-\vec{F}\cdot\vec{v})\,\mathrm{d}t\right] =[P][t] = ML^2T^{-2}</math></center> |
Para el segundo miembro, el primer sumando tiene por dimensiones | Para el segundo miembro, el primer sumando tiene por dimensiones | ||
| Línea 139: | Línea 138: | ||
==Caso (g)== | ==Caso (g)== | ||
| - | |||
| - | + | En este | |
| - | + | <center><math>\vec{r}\times\vec{L} = R^2\vec{p}</math></center> | |
| - | <center><math>( | + | el primer miembro tiene dimensiones de un momento cinético por una distancia |
| + | |||
| + | <center><math>\left[\vec{r}\times\vec{L}\right] = [r][L] = L(ML^2T^{-1}) = ML^3T^{-1}</math></center> | ||
| + | |||
| + | y el segundo de una cantidad de movimiento por una superficie | ||
| + | |||
| + | <center><math>\left[R^2\vec{p}\right] = L^2(MLT^{-1}) = ML^3T^{-1}</math></center> | ||
| + | |||
| + | Puesto que las dimensiones de los miembros son coincidentes, esta fórmula puede ser correcta. Lo que no quiere decir que lo sea. | ||
| - | |||
==Caso (h)== | ==Caso (h)== | ||
| - | + | En el tercer caso | |
| - | <center><math>\ | + | <center><math>\vec{M} = \vec{r}\times\vec{F}+\vec{v}\times\vec{p}</math></center> |
| + | |||
| + | El primer miembro es el momento de una fuerza, que tiene la misma ecuación dimensional que el trabajo | ||
| + | |||
| + | <center><math>[M]= M L^2 T^{-2}\,</math></center> | ||
| + | |||
| + | En el segundo miembro tenemos, para el primer término | ||
| + | |||
| + | <center><math>\left[\vec{r}\times\vec{F}\right] = [r][F]=L(MLT^{-2}) = M L^2T^{-2}</math></center> | ||
| + | |||
| + | y para el segundo | ||
| + | |||
| + | <center><math>\left[\vec{v}\times\vec{p}\right]= [v][p]= (LT^{-1})(MLT^{-1}) = ML^2T^{-2}</math></center> | ||
| + | |||
| + | Puesto que todos los términos tienen las mismas dimensiones, la fórmula puede ser correcta. | ||
| - | |||
[[Categoría:Problemas de introducción a la física (GIE)]] | [[Categoría:Problemas de introducción a la física (GIE)]] | ||
última version al 09:28 26 oct 2013
Contenido |
1 Enunciado
Teniendo en cuenta las dimensiones calculadas en el problema anterior, indique cuáles de las siguientes expresiones son necesariamente incorrectas:
- a)
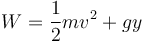
- b)
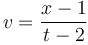
- c)

- d)
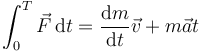
- e)
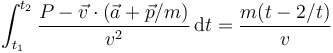
- f)
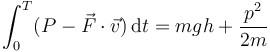
- g)
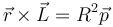
- h)
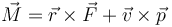
2 Caso (a)
Para que una fórmula sea dimensionalmente correcta los dos miembros de la ecuación deben tener las mismas dimensiones, y lo mismo debe ocurrir con cada uno de los sumandos de las sumas o diferencias que aparezcan en ella.
En el primer caso
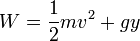
tenemos que el trabajo tiene dimensiones de masa por velocidad al cuadrado
![[W]= M L^2T^{-2}\,](/wiki/images/math/9/7/e/97e5c25fc7da2c830e34ba663f3a050e.png)
De los términos del segundo miembro, el primero tiene claramente las mismas dimensiones que este
![\left[\frac{1}{2}mv^2\right] = [m][v]^2 = M(LT^{-1})^2 = ML^2T^{-2}\,](/wiki/images/math/5/d/3/5d330a85130dd5f038304b71ad2b7d7f.png)
mientras que el segundo tiene las dimensiones de una aceleración por una distancia
![[gy] = [a][y] = \left(LT^{-2}\right)L = L^2T^{-2}\,](/wiki/images/math/3/5/d/35d6a0e6105b84d28031f80efebd7e81.png)
Puesto que aquí no hay ninguna potencia de la masa, que si aparece en los otros dos términos, esta fórmula es necesariamente incorrecta.
3 Caso (b)
La formula
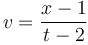
podría parecer correcta a primera vista. Después de todo, la velocidad tiene dimensiones de distancia dividida por tiempo. Sin embargo no es correcta. La razón está en ese “1” y ese “2” del numerador y el denominador. Si no se dice otra cosa, un número, como el 2, es una cantidad adimensional. Por tanto en el denominador estamos restando una cantidad adimensional a una que sí tiene dimensiones (tiempo), lo que viola el principio de homogeneidad.
Para que una fórmula de este tipo (de las que aparecen a menudo en problemas de libros de texto) sea correcta, debe especificarse previamente que se sobreentiende que todas las unidades están en el SI, de forma que el 1 del numerador quiere decir en realidad "1\thinsp;m" y el 2 del denominador es en realidad “2\thinsp;s”.
Si no se hace así, o se usan unidades que no son del SI, es muy posible que los cálculos de un problema conduzcan a error. Por ejemplo, si se dice que la densidad del agua es “1”, y nada más, y se sustituye así en las fórmulas, casi seguro van a obtenerse resultados incorrectos, ya que realmente es “1\thinso;g/cm³” (o, en el SI 1000\thinsp;kg/m³)
4 Caso (c)
En la expresión
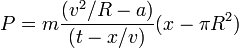
aparecen muchos factores que habría que analizar por separado. Sin embargo, es fácil ver que esta fórmula es incorrecta. En el último factor tenemos la combinación
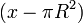
en la cual se suma una longitud (de dimensión L) con un área (de dimensión L2), lo cual es incorrecto y por ello toda la fórmula está mal.
5 Caso (d)
En la fórmula
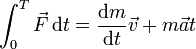
aparece una integral, que no es más que una suma de muchas cantidades muy pequeñas. Como toda suma, los sumandos deben ser dimensionalmente equivalentes y el resultado tiene las mismas dimensiones que cualquiera de ellos. En este caso
![\left[\int_0^T \vec{F}\,\mathrm{d}t\right] = [F][t]=MLT^{-1}](/wiki/images/math/e/b/c/ebccbdd08eabfc7ed27929075a2f2ff1.png)
En el segundo miembro tenemos, para el primer sumando
![\left[\frac{\mathrm{d}m}{\mathrm{d}t}\right] = \frac{[m]}{[t]}[v] = \frac{M}{T}LT^{-1} = M LT^{-2}](/wiki/images/math/2/9/c/29cff534c4e50084837f5255901e8f10.png)
Estas dimensiones no coinciden con las del primer miembro, por lo que ya no hace falta seguir. Esta fórmula es necesariamente incorrecta.
6 Caso (e)
Para la fórmula
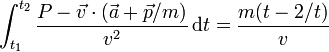
el razonamiento es idéntico al del caso (c). En el numerador del segundo miembro se resta de un tiempo (de dimensión T) la inversa de un tiempo (de dimensión T − 1) lo cual no es admisible y no hace falta seguir.
7 Caso (f)
Para la fórmula
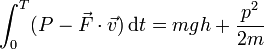
Analizamos en primer lugar el paréntesis del integrando
![[P] = ML^2T^{-3}\,](/wiki/images/math/c/c/8/cc8b1b5b8a4ff00073a550d9c3d8433b.png)
![\left[\vec{F}\cdot\vec{v}\right] = [F][v] = (MLT^{-2})(LT^{-1}) = ML^2T^{-3}](/wiki/images/math/5/c/4/5c43182f1d1fb807b608ed3c832858a8.png)
por lo que la suma es dimensionalmente correcta. Las dimensiones de la integral son
![\left[\int_0^T (P-\vec{F}\cdot\vec{v})\,\mathrm{d}t\right] =[P][t] = ML^2T^{-2}](/wiki/images/math/3/9/3/3939a0a4a49403edb0f275b165c0365c.png)
Para el segundo miembro, el primer sumando tiene por dimensiones
![[mgh] = [m][g][h] = M(LT^{-2})L = ML^2 T^{-2}\,](/wiki/images/math/0/c/2/0c277cf03f546602ca8fb38b0fc77bd3.png)
que son las mismas del primer miembro. Para el segundo sumando
![\left[\frac{p^2}{2m}\right] = \frac{[p]^2}{[m]} = \frac{(MLT^{-1})^2}{M} = ML^2T^{-2}](/wiki/images/math/9/c/8/9c8d9bf36245a228011b96322fdb9246.png)
Por tanto, la fórmula es dimensionalmente correcta.
8 Caso (g)
En este
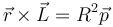
el primer miembro tiene dimensiones de un momento cinético por una distancia
![\left[\vec{r}\times\vec{L}\right] = [r][L] = L(ML^2T^{-1}) = ML^3T^{-1}](/wiki/images/math/d/2/b/d2b042c3d3326959212486577d1e27af.png)
y el segundo de una cantidad de movimiento por una superficie
![\left[R^2\vec{p}\right] = L^2(MLT^{-1}) = ML^3T^{-1}](/wiki/images/math/6/2/b/62bd8a60a26e708fa4bf0bcadc71cc50.png)
Puesto que las dimensiones de los miembros son coincidentes, esta fórmula puede ser correcta. Lo que no quiere decir que lo sea.
9 Caso (h)
En el tercer caso
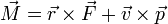
El primer miembro es el momento de una fuerza, que tiene la misma ecuación dimensional que el trabajo
![[M]= M L^2 T^{-2}\,](/wiki/images/math/1/4/4/144d2a88160dd2926991a9df676cce6e.png)
En el segundo miembro tenemos, para el primer término
![\left[\vec{r}\times\vec{F}\right] = [r][F]=L(MLT^{-2}) = M L^2T^{-2}](/wiki/images/math/0/c/0/0c011175100ec19df4d93b9d775e279c.png)
y para el segundo
![\left[\vec{v}\times\vec{p}\right]= [v][p]= (LT^{-1})(MLT^{-1}) = ML^2T^{-2}](/wiki/images/math/d/7/7/d77afe52ba6d9dd89bbf4708e6fc59d4.png)
Puesto que todos los términos tienen las mismas dimensiones, la fórmula puede ser correcta.





