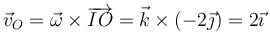Ejemplo gráfico de movimiento plano
De Laplace
(→Velocidad del origen) |
|||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 43: | Línea 43: | ||
Combinando los dos resultados podemos expresar la velocidad del origen en forma vectorial | Combinando los dos resultados podemos expresar la velocidad del origen en forma vectorial | ||
| - | <center><math>\vec{v}_O=2\vec{\imath</math></center> | + | <center><math>\vec{v}_O=2\vec{\imath}</math></center> |
===Mediante el campo de velocidades=== | ===Mediante el campo de velocidades=== | ||
| - | Calculamos en primer lugar la velocidad angular. Puesto que se trata de un movimiento plano, la velocidad angular es ortogonal | + | Calculamos en primer lugar la velocidad angular. Puesto que se trata de un movimiento plano, la velocidad angular es ortogonal a él |
<center><math>\vec{\omega}=\omega\vec{k}</math></center> | <center><math>\vec{\omega}=\omega\vec{k}</math></center> | ||
| Línea 52: | Línea 52: | ||
Relacionamos ahora las velocidades de A y B | Relacionamos ahora las velocidades de A y B | ||
| - | <center><math>\vec{v}_B=\vec{v}_A+\vec{ | + | <center><math>\vec{v}_B=\vec{v}_A+\vec{\omega}\times\overrightarrow{AB}</math></center> |
siendo | siendo | ||
| - | <center><math>\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}= | + | <center><math>\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=4\vec{\imath}-4\vec{\jmath}</math></center> |
lo que nos da | lo que nos da | ||
| - | <center><math> | + | <center><math>2\vec{\imath}+4\vec{\jmath} = -2\vec{\imath}+(\omega\vec{k})\times(4\vec{\imath}-4\vec{\jmath}) = (-2+4\omega)\vec{\imath}+4\omega\vec{\jmath}</math></center> |
Igualando componente a componente | Igualando componente a componente | ||
| - | <center><math> | + | <center><math>2 = -2+4\omega\qquad\qquad 4 = 4\omega\qquad\Rightarrow\qquad \omega = 1</math></center> |
Las dos ecuaciones tienen la misma solución, porque si no no se cumpliría la condición de rigidez. Por tanto | Las dos ecuaciones tienen la misma solución, porque si no no se cumpliría la condición de rigidez. Por tanto | ||
| Línea 70: | Línea 70: | ||
<center><math>\vec{\omega}=\vec{k}</math></center> | <center><math>\vec{\omega}=\vec{k}</math></center> | ||
| - | Una vez que tenemos la velocidad angular, hallamos la velocidad del punto O a partir de la de | + | Una vez que tenemos la velocidad angular, hallamos la velocidad del punto O a partir de la de A |
| - | <center><math>\vec{v}_O = \vec{v} | + | <center><math>\vec{v}_O = \vec{v}_A+\vec{\omega}\times\overrightarrow{AO}=-2\vec{\imath}+(\vec{k}\times(-4\vec{\jmath})=(-2+4)\vec{\imath}=2\vec{\imath}</math></center> |
==Centro instantáneo de rotación== | ==Centro instantáneo de rotación== | ||
| + | La posición del CIR la podemos determinar tanto analítica como geométricamente. | ||
| + | |||
| + | ===Determinación analítica=== | ||
| + | En un movimiento plano, la posición del CIR respecto a un punto A del que conocemos la velocidad es | ||
| + | |||
| + | <center><math>\overrightarrow{AI}=\frac{\vec{\omega}\times\vec{v}_A}{|\vec{\omega}|^2}</math></center> | ||
| + | |||
| + | En nuestro caso, empleando la velocidad angular que ya calculamos | ||
| + | |||
| + | <center><math>\overrightarrow{AI}=\frac{\vec{k}\times(-2\vec{\imath})}{1}=-2\vec{\jmath}</math></center> | ||
| + | |||
| + | Esta es la posición respecto al punto A. Respecto al origen de coordenadas será | ||
| + | |||
| + | <center><math>\overrightarrow{OI}=\overrightarrow{OA}+\overrightarrow{AI}=4\vec{\jmath}-2\vec{\jmath} = 2\vec{\jmath}</math></center> | ||
| + | |||
| + | ===Determinación geométrica=== | ||
| + | Para hallar geométricamente la posición del CIR observamos que, para todo punto P se cumple | ||
| + | |||
| + | <center><math>\vec{v}_P = \vec{\omega}\times\overrightarrow{IP}</math></center> | ||
| + | |||
| + | la velocidad de cada punto es ortogonal al vector de posición relativo respecto al CIR. | ||
| + | |||
| + | Trazamos entonces las perpendiculares a las velocidades <math>\vec{v}_A</math> y <math>\vec{v}_B</math> por los puntos respectivos. El CIR se halla en la interesección de estas dos perpendiculares. En este caso este punto tiene por vector de posición | ||
| + | |||
| + | <center><math>\overrightarrow{OI}=2\vec{\jmath}</math></center> | ||
| + | |||
| + | <center>[[Archivo:ejemplo-calculo-cir.png]]</center> | ||
| + | |||
| + | ===Velocidad del origen=== | ||
| + | Una vez que tenemos localizado el CIR y conocemos la velocidad angular, podemos hallar la velocidad de cualquier punto. Para el origen de coordenadas | ||
| + | |||
| + | <center><math>\vec{v}_O = \vec{\omega}\times\overrightarrow{IO}=\vec{k}\times(-2\vec{\jmath})=2\vec{\imath}</math></center> | ||
| + | |||
[[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | [[Categoría:Problemas de cinemática del sólido rígido (GIE)]] | ||
| + | [[Categoría:Problemas de cinemática del sólido rígido]] | ||
última version al 10:46 24 sep 2015
Contenido[ocultar] |
1 Enunciado
En un movimiento plano, se tiene que la velocidad instantánea de dos puntos A y B es la ilustrada en la figura (para la posición, la cuadrícula representa cm y para la velocidad cm/s)

- En dicho instante, ¿cuál es la velocidad del origen de coordenadas O?
- ¿Dónde se encuentra el centro instantáneo de rotación?
2 Nota sobre unidades
En lo que sigue, todas las distancias se miden en cm, las velocidades en cm/s y las velocidades angulares en rad/s.
3 Velocidad del origen
Podemos hallar la velocidad del punto O:
- Aplicando la condición cinemática de rigidez
- Mediante la fórmula del campo de velocidades
- Gráfica o analíticamente una vez localizado el CIR
3.1 Condición de rigidez
La velocidad del origen la podemos escribir como
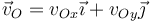
Esta velocidad debe cumplir, junto con la del punto A, la condición de rigidez o de equiproyectividad
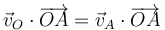
donde
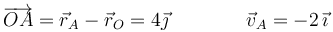
lo que nos da una componente de la velocidad del origen
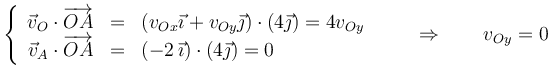
De manera análoga, tenemos, para el punto B
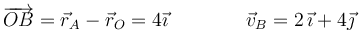
y
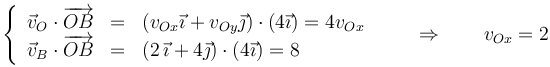
Combinando los dos resultados podemos expresar la velocidad del origen en forma vectorial
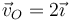
3.2 Mediante el campo de velocidades
Calculamos en primer lugar la velocidad angular. Puesto que se trata de un movimiento plano, la velocidad angular es ortogonal a él
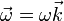
Relacionamos ahora las velocidades de A y B
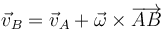
siendo
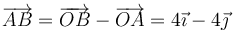
lo que nos da
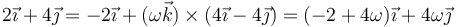
Igualando componente a componente
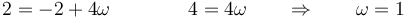
Las dos ecuaciones tienen la misma solución, porque si no no se cumpliría la condición de rigidez. Por tanto
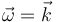
Una vez que tenemos la velocidad angular, hallamos la velocidad del punto O a partir de la de A
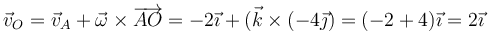
4 Centro instantáneo de rotación
La posición del CIR la podemos determinar tanto analítica como geométricamente.
4.1 Determinación analítica
En un movimiento plano, la posición del CIR respecto a un punto A del que conocemos la velocidad es
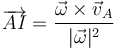
En nuestro caso, empleando la velocidad angular que ya calculamos
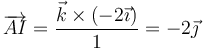
Esta es la posición respecto al punto A. Respecto al origen de coordenadas será
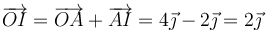
4.2 Determinación geométrica
Para hallar geométricamente la posición del CIR observamos que, para todo punto P se cumple
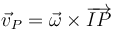
la velocidad de cada punto es ortogonal al vector de posición relativo respecto al CIR.
Trazamos entonces las perpendiculares a las velocidades 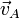 y
y 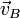 por los puntos respectivos. El CIR se halla en la interesección de estas dos perpendiculares. En este caso este punto tiene por vector de posición
por los puntos respectivos. El CIR se halla en la interesección de estas dos perpendiculares. En este caso este punto tiene por vector de posición
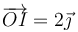
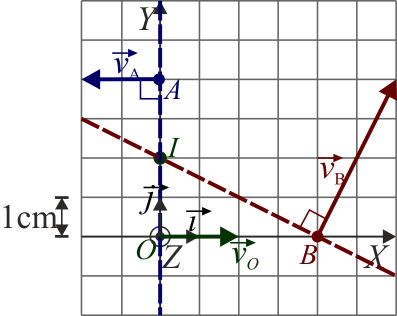
4.3 Velocidad del origen
Una vez que tenemos localizado el CIR y conocemos la velocidad angular, podemos hallar la velocidad de cualquier punto. Para el origen de coordenadas