Propiedades de un sistema de 8 partículas
De Laplace
(Página creada con '==Enunciado== Para los movimientos compatibles del problema “Clasificación de movimientos de un sólido” calcule la cantidad de movimiento, el momento cinético…') |
(→Cantidad de movimiento) |
||
| (8 ediciones intermedias no se muestran.) | |||
| Línea 3: | Línea 3: | ||
<center>[[Archivo:ocho-masas.png]]</center> | <center>[[Archivo:ocho-masas.png]]</center> | ||
| + | |||
| + | respecto al sistema de ejes de la figura. | ||
==Introducción== | ==Introducción== | ||
| - | Este problema combina la solución de otros dos problemas. Por un lado, en “[[Clasificación de movimientos de un sólido]]” se establecen las propiedades cinemáticas de varios conjuntos de velocidades de tres puntos de un sólido. En segundo lugar, en | + | Este problema combina la solución de otros dos problemas. Por un lado, en “[[Clasificación de movimientos de un sólido]]” se establecen las propiedades cinemáticas de varios conjuntos de velocidades de tres puntos de un sólido. En segundo lugar, en “[[Momento de inercia de un sistema de partículas]]”, se halla el momento de inercia de un sistema de ocho partículas como el que se emplea en este problema. |
| + | |||
| + | La técnica general en lo que sigue es: | ||
| + | |||
| + | ;Cantidad de movimiento: Para un sistema de partículas se cumple | ||
| + | |||
| + | <center><math>\vec{p}=M\vec{v}_C</math></center> | ||
| + | |||
| + | :donde <math>M</math> es la masa total del sistema y <math>\vec{v}_C</math> la velocidad de su centro de masas, la cual se puede calcular como la de un punto más del sólido | ||
| + | |||
| + | <center><math>\vec{v}_C=\vec{v}_A+\vec{\omega}\times\overrightarrow{AC}</math></center> | ||
| + | ;Momento cinético: El momento de n sistema de partículas vale | ||
| + | |||
| + | <center><math>\vec{L}_O=M\vec{r}_C\times\vec{v}_C+\vec{L}_C</math></center> | ||
| + | |||
| + | :que en el caso particular de un sólido se convierte en | ||
| + | |||
| + | <center><math>\vec{L}_O=M\vec{r}_C\times\vec{v}_C+I\vec{\omega}</math></center> | ||
| + | |||
| + | :siendo I el momento de inercia respecto a un eje paralelo al EIRMD y que pasa por el centro de masas. En el caso de esta distribución de ocho masas, tal como se ve en otro problema, el momento de inercia es el mismo sea cual sea la dirección y vale | ||
| + | |||
| + | <center><math>I=4mb^2\,</math></center> | ||
| + | |||
| + | ;Energía cinética: El tratamiento es similar al del momento cinético. la energía cinética de este sólido vale | ||
| + | |||
| + | <center><math>K=\frac{1}{2}M|\vec{v}_C|^2+\frac{1}{2}I|\vec{\omega}|^2</math></center> | ||
| + | |||
| + | ==Resumen de los distintos casos== | ||
| + | En el problema de cinemática correspondiente se parte de que los puntos | ||
| + | |||
| + | <center><math>\overrightarrow{OA}=b\vec{\imath}\qquad\overrightarrow{OB}=b\vec{\jmath}\qquad\overrightarrow{OP}=b\vec{k}</math></center> | ||
| + | |||
| + | con <math>b=10\,\mathrm{cm}</math> tienen las velocidades | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Caso | ||
| + | ! <math>\vec{v}_A</math> (cm/s) | ||
| + | ! <math>\vec{v}_B</math> (cm/s) | ||
| + | ! <math>\vec{v}_P</math> (cm/s) | ||
| + | |- | ||
| + | ! I | ||
| + | | <math>\vec{\jmath}-\vec{k}</math> | ||
| + | | <math>-\vec{\imath}+\vec{k}</math> | ||
| + | | <math>\vec{\imath}-\vec{\jmath}</math> | ||
| + | |- | ||
| + | ! II | ||
| + | | <math>\vec{\imath}+\vec{\jmath}-\vec{k}</math> | ||
| + | | <math>\vec{k}</math> | ||
| + | | <math>2\vec{\imath}-\vec{\jmath}</math> | ||
| + | |- | ||
| + | ! III | ||
| + | | <math>\vec{\jmath}-\vec{k}</math> | ||
| + | | <math>-\vec{\imath}+\vec{k}</math> | ||
| + | | <math>\vec{\imath}-\vec{\jmath}+\vec{k}</math> | ||
| + | |- | ||
| + | ! IV | ||
| + | | <math>\vec{\imath}-\vec{\jmath}</math> | ||
| + | | <math>\vec{\imath}-\vec{\jmath}</math> | ||
| + | | <math>\vec{\imath}-\vec{\jmath}</math> | ||
| + | |- | ||
| + | ! V | ||
| + | | <math>\vec{\imath}+2\vec{\jmath}</math> | ||
| + | | <math>\vec{\jmath}+2\vec{k}</math> | ||
| + | | <math>2\vec{\imath}+\vec{k}</math> | ||
| + | |- | ||
| + | ! VI | ||
| + | | <math>\vec{\imath}+\vec{\jmath}+\vec{k}</math> | ||
| + | | <math>\vec{\imath}+\vec{\jmath}+\vec{k}</math> | ||
| + | | <math>\vec{0}</math> | ||
| + | |} | ||
| + | |||
| + | Para estos casos,se calcula la velocidad angular del sólido, siendo el resultado | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Caso | ||
| + | ! <math>\vec{\omega}</math> (rad/s) | ||
| + | |- | ||
| + | ! I | ||
| + | | <math>\frac{1}{10}\left(\vec{\imath}+\vec{\jmath}+\vec{k}\right)</math> | ||
| + | |- | ||
| + | ! II | ||
| + | | <math>\frac{1}{10}\left(\vec{\imath}+\vec{\jmath}+\vec{k}\right)</math> | ||
| + | |- | ||
| + | ! IV | ||
| + | | <math>\vec{0}</math> | ||
| + | |- | ||
| + | ! V | ||
| + | |<math>\frac{1}{10}\left(\vec{\imath}+\vec{\jmath}+\vec{k}\right)</math> | ||
| + | |- | ||
| + | ! VI | ||
| + | |<math>\frac{1}{10}\left(\vec{\imath}-\vec{\jmath}\right)</math> | ||
| + | |} | ||
| + | |||
| + | ==Cantidad de movimiento== | ||
| + | La masa del sistema es la misma en todos los casos | ||
| + | |||
| + | <center><math>M=8m=800\,\mathrm{g}</math></center> | ||
| + | |||
| + | por lo que solo precisamos calcular la velocidad del centro de masas en cada caso. El vector de posición relativa respecto al punto A es | ||
| + | |||
| + | <center><math>\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}=(5\vec{\imath}+5\vec{\jmath}+5\vec{k})-10\vec{\imath}=-5\vec{\imath}+5\vec{\jmath}+5\vec{k}</math></center> | ||
| + | |||
| + | Así obtenemos, para la velocidad del CM en cada uno de los 5 casos posibles | ||
| + | |||
| + | {| class="bordeado" | ||
| + | |- | ||
| + | ! Caso | ||
| + | ! <math>\vec{v}_A</math> (cm/s) | ||
| + | ! <math>\vec{\omega}</math> (rad/s) | ||
| + | ! <math>\vec{v}_C</math> (cm/s) | ||
| + | ! <math>\vec{p}</math> (kg·cm/s) | ||
| + | |- | ||
| + | ! I | ||
| + | | <math>\vec{\jmath}-\vec{k}</math> | ||
| + | | <math>\frac{1}{10}\left(\vec{\imath}+\vec{\jmath}+\vec{k}\right)</math> | ||
| + | | <math>\vec{0}</math> | ||
| + | | <math>\vec{0}</math> | ||
| + | |- | ||
| + | ! II | ||
| + | | <math>\vec{\imath}+\vec{\jmath}-\vec{k}</math> | ||
| + | | <math>\frac{1}{10}\left(\vec{\imath}+\vec{\jmath}+\vec{k}\right)</math> | ||
| + | | <math>\vec{\imath}</math> | ||
| + | | <math>0.8\vec{\imath}</math> | ||
| + | |- | ||
| + | ! IV | ||
| + | | <math>\vec{\imath}-\vec{\jmath}</math> | ||
| + | | <math>\vec{0}</math> | ||
| + | | <math>\vec{\imath}-\vec{\jmath}</math> | ||
| + | | <math>0.8\vec{\imath}-0.8\vec{\jmath}</math> | ||
| + | |- | ||
| + | ! V | ||
| + | | <math>\vec{\imath}+2\vec{\jmath}</math> | ||
| + | |<math>\frac{1}{10}\left(\vec{\imath}+\vec{\jmath}+\vec{k}\right)</math> | ||
| + | | <math>\vec{\imath}+\vec{\jmath}+\vec{k}</math> | ||
| + | | <math>0.8\vec{\imath}+0.8\vec{\jmath}+0.8\vec{k}</math> | ||
| + | |- | ||
| + | ! VI | ||
| + | | <math>\vec{\imath}+\vec{\jmath}+\vec{k}</math> | ||
| + | |<math>\frac{1}{10}\left(\vec{\imath}-\vec{\jmath}\right)</math> | ||
| + | | <math>0.5\vec{\imath}+0.5\vec{\jmath}+\vec{k}</math> | ||
| + | | <math>0.4\vec{\imath}+0.4\vec{\jmath}+0.8\vec{k}</math> | ||
| + | |} | ||
| + | |||
| + | |||
[[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | [[Categoría:Problemas de dinámica del sólido rígido (GIE)]] | ||
última version al 18:17 31 dic 2013
Contenido |
1 Enunciado
Para los movimientos compatibles del problema “Clasificación de movimientos de un sólido” calcule la cantidad de movimiento, el momento cinético y la energía cinética del sistema de masas.
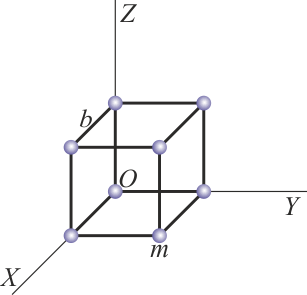
respecto al sistema de ejes de la figura.
2 Introducción
Este problema combina la solución de otros dos problemas. Por un lado, en “Clasificación de movimientos de un sólido” se establecen las propiedades cinemáticas de varios conjuntos de velocidades de tres puntos de un sólido. En segundo lugar, en “Momento de inercia de un sistema de partículas”, se halla el momento de inercia de un sistema de ocho partículas como el que se emplea en este problema.
La técnica general en lo que sigue es:
- Cantidad de movimiento
- Para un sistema de partículas se cumple

- donde M es la masa total del sistema y
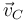 la velocidad de su centro de masas, la cual se puede calcular como la de un punto más del sólido
la velocidad de su centro de masas, la cual se puede calcular como la de un punto más del sólido
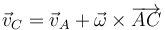
- Momento cinético
- El momento de n sistema de partículas vale

- que en el caso particular de un sólido se convierte en
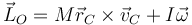
- siendo I el momento de inercia respecto a un eje paralelo al EIRMD y que pasa por el centro de masas. En el caso de esta distribución de ocho masas, tal como se ve en otro problema, el momento de inercia es el mismo sea cual sea la dirección y vale
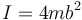
- Energía cinética
- El tratamiento es similar al del momento cinético. la energía cinética de este sólido vale
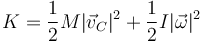
3 Resumen de los distintos casos
En el problema de cinemática correspondiente se parte de que los puntos
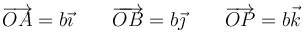
con 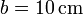 tienen las velocidades
tienen las velocidades
| Caso | 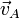 (cm/s) (cm/s)
| 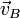 (cm/s) (cm/s)
| 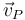 (cm/s) (cm/s)
|
|---|---|---|---|
| I | 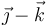
| 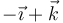
| 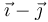
|
| II | 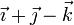
| 
| 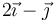
|
| III | 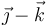
| 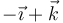
| 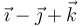
|
| IV | 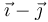
| 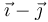
| 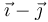
|
| V | 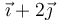
| 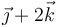
| 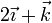
|
| VI | 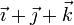
| 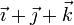
| 
|
Para estos casos,se calcula la velocidad angular del sólido, siendo el resultado
| Caso |  (rad/s) (rad/s)
|
|---|---|
| I | 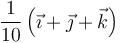
|
| II | 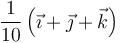
|
| IV | 
|
| V | 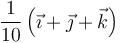
|
| VI | 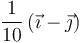
|
4 Cantidad de movimiento
La masa del sistema es la misma en todos los casos
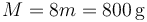
por lo que solo precisamos calcular la velocidad del centro de masas en cada caso. El vector de posición relativa respecto al punto A es
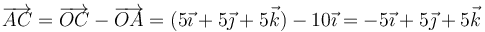
Así obtenemos, para la velocidad del CM en cada uno de los 5 casos posibles
| Caso | 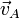 (cm/s) (cm/s)
|  (rad/s) (rad/s)
| 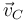 (cm/s) (cm/s)
| 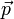 (kg·cm/s) (kg·cm/s)
|
|---|---|---|---|---|
| I | 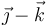
| 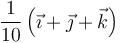
| 
| 
|
| II | 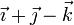
| 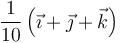
| 
| 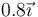
|
| IV | 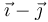
| 
| 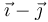
| 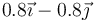
|
| V | 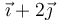
| 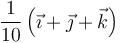
| 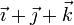
| 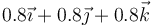
|
| VI | 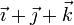
| 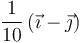
| 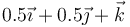
| 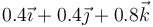
|





