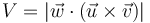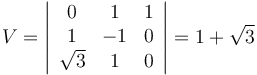Cuestión de álgebra vectorial, Noviembre 2012 (F1 GIA)
De Laplace
(→Solución) |
(→Enunciado) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | [[Archivo:paralelep_PC1_1.gif|right]]Los puntos <math>O</math>, <math>A</math>, <math>B</math> y <math>C</math> son vértices no contiguos de un paralelepípedo, de manera que <math>O</math> y <math>A</math> se encuentran en un plano distinto al que contiene a <math>B</math> y <math>C</math>. Las coordenadas de estos puntos en un sistema de | + | [[Archivo:paralelep_PC1_1.gif|right]]Los puntos <math>O</math>, <math>A</math>, <math>B</math> y <math>C</math> son vértices no contiguos de un paralelepípedo, de manera que <math>O</math> y <math>A</math> se encuentran en un plano distinto al que contiene a <math>B</math> y <math>C</math>. Las coordenadas de estos puntos en un sistema de referencia cartesiano son: |
| - | referencia cartesiano son: | + | |
<center><math>O(0, 0, 0)\mathrm{;}\quad A(\sqrt{3} + 1, 0,0)\mathrm{;}\quad B(1, 0, 1)\mathrm{;}\quad C(\sqrt{3}, 2, 1)\mathrm{,} | <center><math>O(0, 0, 0)\mathrm{;}\quad A(\sqrt{3} + 1, 0,0)\mathrm{;}\quad B(1, 0, 1)\mathrm{;}\quad C(\sqrt{3}, 2, 1)\mathrm{,} | ||
última version al 18:20 23 sep 2013
1 Enunciado
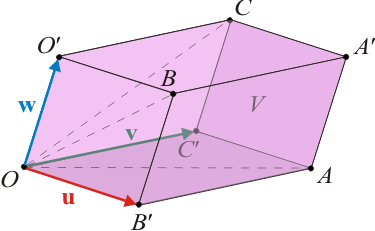
Los puntos O, A, B y C son vértices no contiguos de un paralelepípedo, de manera que O y A se encuentran en un plano distinto al que contiene a B y C. Las coordenadas de estos puntos en un sistema de referencia cartesiano son: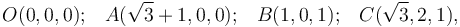
medidas en unidades de longitud. Determine las componentes cartesianas de los vectores
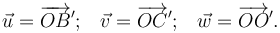
y calcule el volumen del paralelepípedo.
2 Solución
Para resolver este sencillo ejercicio basta con aplicar las definiciones y propiedades de los dos operaciones que dotan de estructura de espacio vectorial al conjunto de los segmentos orientados en 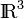 , ordenados como vectores libres. Como se sabe, dichas operaciones son la suma de vectores (según la ley del paralelogramo), y el producto de un vector por un escalar (en general, un número real).
, ordenados como vectores libres. Como se sabe, dichas operaciones son la suma de vectores (según la ley del paralelogramo), y el producto de un vector por un escalar (en general, un número real).
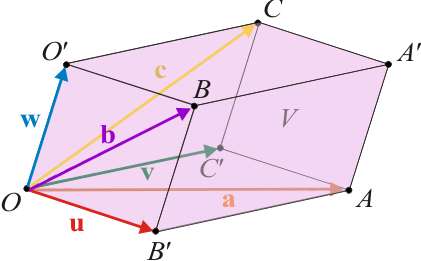
Definamos los vectores  ,
,  y
y 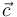 , que tienen la dirección, el sentido y el módulo de los segmentos orientados
, que tienen la dirección, el sentido y el módulo de los segmentos orientados  ,
, 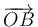 y
y  :
:
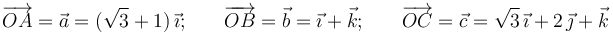
Obsérvese que, según la definición geométrica de la suma de vectores, se verificarán las siguientes relaciones:
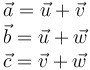
Por tanto, si al vector  le sumamos el opuesto del vector
le sumamos el opuesto del vector 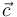 , se tendrá...
, se tendrá...
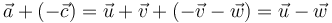
Y si al vector resultante se le suma el vector  , se obtiene:
, se obtiene:


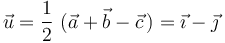
Utilizando la primera relación que introdujimos anteriormente, podemos determinar el vector  sumándole a
sumándole a  el opuesto de
el opuesto de  :
:


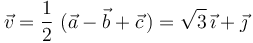
Finalmente, el vector 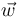 lo podemos obtener de la segunda relación:
lo podemos obtener de la segunda relación:
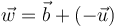


Para calcular el valor del volumen del paralelepípedo, tenemos en cuenta que los vectores calculados,  ,
,  y
y 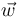 , se corresponden con tres segmentos orientados formados a partir de tres aristas adyacentes del paralelepípedo. En consecuencia, el valor absoluto del producto mixto de aquellos vectores es igual al volumen V que se demanda:
, se corresponden con tres segmentos orientados formados a partir de tres aristas adyacentes del paralelepípedo. En consecuencia, el valor absoluto del producto mixto de aquellos vectores es igual al volumen V que se demanda: