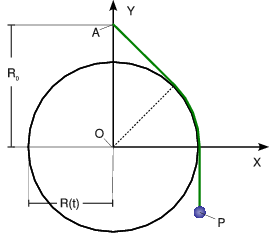
Entrar Página Discusión Historial Go to the site toolbox

Cuerda sobre disco de radio variable

De Laplace

(Diferencias entre revisiones)
(Página creada con '== Enunciado == right Un punto material <math>P</math> pende verticalmente del extremo de un hilo inextensible y permanent…')
(→Velocidad y aceleración)
 
(Una edición intermedia no se muestra.)
Línea 9: Línea 9:
=== Ecuaciones horarias del punto P===
=== Ecuaciones horarias del punto P===
-
 
+
[[Imagen:Circunferencia_radio_variable_angulos.png|right]]
Nuestro primer objetivo es encontrar el vector de posición del punto <math>P </math>. Podemos construir ese vector de la siguiente manera
Nuestro primer objetivo es encontrar el vector de posición del punto <math>P </math>. Podemos construir ese vector de la siguiente manera
<center>
<center>
Línea 17: Línea 17:
</math>
</math>
</center>
</center>
-
Los puntos <math>A </math>, <math>B </math> y <math>C </math> están indicados en la figura.
 
Para el vector <math>\overrightarrow{OC} </math> tenemos
Para el vector <math>\overrightarrow{OC} </math> tenemos
Línea 32: Línea 31:
</center>
</center>
El módulo <math>|\overrightarrow{CP}| </math> es la longitud de la cuerda menos la longitud del segmento <math>\overline{AB} </math> y del arco <math>\stackrel\frown {BC} </math>.  
El módulo <math>|\overrightarrow{CP}| </math> es la longitud de la cuerda menos la longitud del segmento <math>\overline{AB} </math> y del arco <math>\stackrel\frown {BC} </math>.  
 +
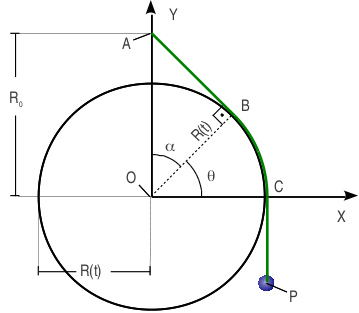
Los puntos <math>A </math>, <math>B </math> y <math>C </math> están indicados en la figura.
En la figura vemos los ángulos <math>\theta</math> y <math>\alpha </math>, con
En la figura vemos los ángulos <math>\theta</math> y <math>\alpha </math>, con
Línea 92: Línea 92:
</math>
</math>
</center>
</center>
 +
 +
=== Velocidad y aceleración===
 +
La velocidad es la derivada respecto del tiempo del vector de posición
 +
<center>
 +
<math>
 +
\vec{v}_P = \dot{\overrightarrow{OP}} =
 +
R_0\,\omega\cos(\omega t)\,\vec{\imath} + R_0\omega^2 t\cos(\omega t)\,\vec{\jmath}
 +
</math>
 +
</center>
 +
La aceleración es la derivada respecto del tiempo del vector velocidad
 +
<center>
 +
<math>
 +
\vec{a}_P = \dot{\vec{v}} =
 +
-R_0\omega^2\,\mathrm{sen}\,(\omega t)\,\vec{\imath} +
 +
R_0w^2\,(\cos(\omega t) - \omega t\,\mathrm{sen}\,(\omega t))\,\vec{\jmath}
 +
</math>
 +
</center>
 +
 +
=== Radio de curvatura===
 +
El radio de curvatura en cada punto de la trayectoria es
 +
<center>
 +
<math>
 +
R_{\kappa} = \dfrac{|\vec{v}|^2}{a_N}
 +
</math>
 +
</center>
 +
Como tenemos el vector velocidad expresado en una base cartesiana, podemos calcular su módulo
 +
<center>
 +
<math>
 +
|\vec{v}(t)| = R_0\omega\sqrt{1+\omega^2t^2}\cos(\omega t)
 +
</math>
 +
</center>
 +
La aceleración normal es
 +
<center>
 +
<math>
 +
a_N = \dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|}
 +
=
 +
\dfrac{R_0\omega^2\cos(\omega t)}{\sqrt{1+\omega^2t^2}}
 +
</math>
 +
</center>
 +
Con lo que el radio de curvatura es
 +
<center>
 +
<math>
 +
R_{\kappa}(t) = R_0\,\left(1+w^2t^2\right)^{3/2}\cos(\omega t)
 +
</math>
 +
</center>
 +
La posición del centro de curvatura en cada instante es
 +
<center>
 +
<math>
 +
\vec{r}_{\kappa}(t) = \overrightarrow{OP} + R_{\kappa}\vec{N}
 +
</math>
 +
</center>
 +
Nos lo piden sólo en el instante inicial, así que sólo tenemos que calcular el vector normal en el instante inicial. El vector normal es
 +
<center>
 +
<math>
 +
\vec{N} = \dfrac{\vec{a}-a_T\vec{T}}{a_N}
 +
</math>
 +
</center>
 +
En el instante inicial tenemos
 +
<center>
 +
<math>
 +
\begin{array}{l}
 +
\overrightarrow{OP}(0) = -R_0\,\left(\dfrac{\pi}{2}-1\right)\,\vec{\jmath}\\
 +
\\
 +
\vec{v}_P(0) = R_0\omega\,\vec{\imath}\\
 +
\\
 +
\vec{a}_P(0) = R_0\omega^2\,\vec{\jmath}\\
 +
\\
 +
a_N(0) = R_0\omega^2\\
 +
\\
 +
R_{\kappa}(0) = R_0
 +
\end{array}
 +
</math>
 +
</center>
 +
En ese instante el vector tangente es
 +
<center>
 +
<math>
 +
\vec{T}(0) = \vec{\imath}
 +
</math>
 +
</center>
 +
La aceleración tangencial es
 +
<center>
 +
<math>
 +
a_T(0) = \vec{a}(0)\cdot\vec{T}(0) = 0
 +
</math>
 +
</center>
 +
Por tanto el vector normal es
 +
<center>
 +
<math>
 +
\vec{N}(0) = \dfrac{\vec{a}}{a_N} = \vec{\jmath}
 +
</math>
 +
</center>
 +
El vector de posición del centro de curvatura en ese instante inicial es
 +
<center>
 +
<math>
 +
\vec{r}_{O_{\kappa}}(0) = \dfrac{4-\pi}{2}\,R_0\,\vec{\jmath}
 +
</math>
 +
</center>
 +
Este punto está sobre el eje <math>OY </math>, un poquito por encima del origen.

última version al 17:41 29 oct 2012

Contenido

1 Enunciado

Un punto material P pende verticalmente del extremo de un hilo inextensible y permanentemente tenso. Este se apoya y desliza sobre una circunferencia de radio variable con el tiempo 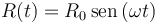R(t) = R_0\,\mathrm{sen}\,(\omega t) en el intervalo 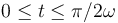0\leq t\leq\pi/2\omega (R0 y ω son constantes conocidas), y centrada en el origen O de un sistema de referencia cartesiano OXY . La longitud total del hilo es l = πR0 / 2, y su otro extremo se halla fijo en un punto A, tal que 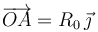\overrightarrow{OA} = R_0 \,\vec{\jmath} (ver figura). Determina:

  1. Las ecuaciones horarias cartesianas del punto P , y su posición final en el instante final tf = π / 2ω.
  2. Los vectores velocidad y aceleración de dicho punto en todo instante de tiempo.
  3. La aceleración normal de P y el radio de curvatura de su trayectoria en todo instante de tiempo, así como la posición del centro de curvatura de la trayectoria en el instante inicial.

2 Solución

2.1 Ecuaciones horarias del punto P

Nuestro primer objetivo es encontrar el vector de posición del punto P. Podemos construir ese vector de la siguiente manera

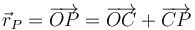
\vec{r}_P = \overrightarrow{OP} = \overrightarrow{OC} + \overrightarrow{CP}

Para el vector \overrightarrow{OC} tenemos

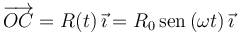
\overrightarrow{OC} = R(t)\,\vec{\imath} = R_0\,\mathrm{sen}\,(\omega t)\,\vec{\imath}

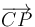Para el vector \overrightarrow{CP} tenemos

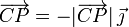
\overrightarrow{CP} = -|\overrightarrow{CP}|\,\vec{\jmath}

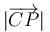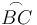El módulo |\overrightarrow{CP}| es la longitud de la cuerda menos la longitud del segmento \overline{AB} y del arco \stackrel\frown {BC} . Los puntos A, B y C están indicados en la figura.

En la figura vemos los ángulos θ y α, con

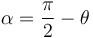
\alpha = \dfrac{\pi}{2}-\theta

Del triángulo rectángulo OBA tenemos

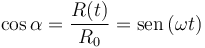
\cos{\alpha} = \dfrac{R(t)}{R_0} = \mathrm{sen}\,(\omega t)

Por otro lado

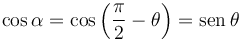
\cos{\alpha} = \cos\left(\dfrac{\pi}{2}-\theta\right) = \mathrm{sen}\,\theta

Igualando las dos expresiones obtenemos

θ = ωt

La longitud del segmento \overline{AB} es

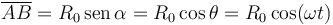
\overline{AB} = R_0\,\mathrm{sen}\,\alpha = R_0\cos\theta = R_0\cos(\omega t)

Mientras que la longitud del arco es

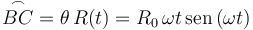
\stackrel\frown{BC} = \theta\,R(t) = R_0\,\omega t\,\mathrm{sen}\,(\omega t)

Por tanto, el módulo 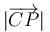|\overrightarrow{CP}| es

|\overrightarrow{CP}| = l - R_0\cos(\omega t) - R_0\,\omega t\,\mathrm{sen}\,(\omega t) = R_0\,\left(\dfrac{\pi}{2} - \cos(\omega t) - \omega t\,\mathrm{sen}\,(\omega t)\right)

Y el vector de posición de la partícula es

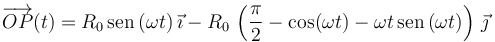
\overrightarrow{OP}(t) = R_0\,\mathrm{sen}\,(\omega t)\,\vec{\imath} -R_0\,\left(\dfrac{\pi}{2} - \cos(\omega t) - \omega t\,\mathrm{sen}\,(\omega t)\right) \,\vec{\jmath}

En el instante tf = π / 2ω el valor de este vector es

\overrightarrow{OP}(t_f) = R_0\,\vec{\imath}

2.2 Velocidad y aceleración

La velocidad es la derivada respecto del tiempo del vector de posición

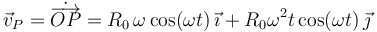
\vec{v}_P = \dot{\overrightarrow{OP}} = R_0\,\omega\cos(\omega t)\,\vec{\imath} + R_0\omega^2 t\cos(\omega t)\,\vec{\jmath}

La aceleración es la derivada respecto del tiempo del vector velocidad

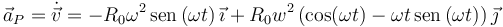
\vec{a}_P = \dot{\vec{v}} = -R_0\omega^2\,\mathrm{sen}\,(\omega t)\,\vec{\imath} + R_0w^2\,(\cos(\omega t) - \omega t\,\mathrm{sen}\,(\omega t))\,\vec{\jmath}

2.3 Radio de curvatura

El radio de curvatura en cada punto de la trayectoria es

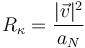
R_{\kappa} = \dfrac{|\vec{v}|^2}{a_N}

Como tenemos el vector velocidad expresado en una base cartesiana, podemos calcular su módulo

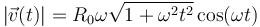
|\vec{v}(t)| = R_0\omega\sqrt{1+\omega^2t^2}\cos(\omega t)

La aceleración normal es

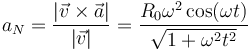
a_N = \dfrac{|\vec{v}\times\vec{a}|}{|\vec{v}|} = \dfrac{R_0\omega^2\cos(\omega t)}{\sqrt{1+\omega^2t^2}}

Con lo que el radio de curvatura es

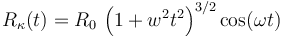
R_{\kappa}(t) = R_0\,\left(1+w^2t^2\right)^{3/2}\cos(\omega t)

La posición del centro de curvatura en cada instante es

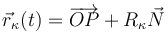
\vec{r}_{\kappa}(t) = \overrightarrow{OP} + R_{\kappa}\vec{N}

Nos lo piden sólo en el instante inicial, así que sólo tenemos que calcular el vector normal en el instante inicial. El vector normal es

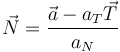
\vec{N} = \dfrac{\vec{a}-a_T\vec{T}}{a_N}

En el instante inicial tenemos

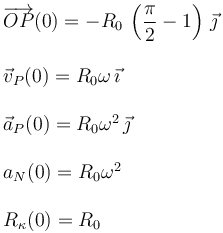
\begin{array}{l} \overrightarrow{OP}(0) = -R_0\,\left(\dfrac{\pi}{2}-1\right)\,\vec{\jmath}\\ \\ \vec{v}_P(0) = R_0\omega\,\vec{\imath}\\ \\ \vec{a}_P(0) = R_0\omega^2\,\vec{\jmath}\\ \\ a_N(0) = R_0\omega^2\\ \\ R_{\kappa}(0) = R_0 \end{array}

En ese instante el vector tangente es

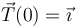
\vec{T}(0) = \vec{\imath}

La aceleración tangencial es

a_T(0) = \vec{a}(0)\cdot\vec{T}(0) = 0

Por tanto el vector normal es

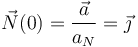
\vec{N}(0) = \dfrac{\vec{a}}{a_N} = \vec{\jmath}

El vector de posición del centro de curvatura en ese instante inicial es

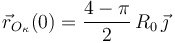
\vec{r}_{O_{\kappa}}(0) = \dfrac{4-\pi}{2}\,R_0\,\vec{\jmath}

Este punto está sobre el eje OY, un poquito por encima del origen.

Obtenido de "http://tesla.us.es/wiki/index.php/Cuerda_sobre_disco_de_radio_variable"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 17:41, 29 oct 2012. - Esta página ha sido visitada 3.666 veces. - Aviso legal - Acerca de Laplace