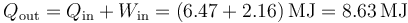Refrigeración de una habitación
De Laplace
| (5 ediciones intermedias no se muestran.) | |||
| Línea 24: | Línea 24: | ||
Puesto que las puertas y ventanas están cerradas, se trata de un proceso a volumen constante, por el que el calor que entra en el sistema es | Puesto que las puertas y ventanas están cerradas, se trata de un proceso a volumen constante, por el que el calor que entra en el sistema es | ||
| - | <center><math>Q = nc_v(T_f- | + | <center><math>Q = nc_v(T_f-T_i)\,</math></center> |
siendo | siendo | ||
| Línea 32: | Línea 32: | ||
y el calor | y el calor | ||
| - | <center><math>Q = 17300\times 20.785\times (-18)\,\mathrm{J}=- | + | <center><math>Q = 17300\times 20.785\times (-18)\,\mathrm{J}=-6.47\,\mathrm{MJ}</math></center> |
puesto que se nos pide el calor que sale de la habitación | puesto que se nos pide el calor que sale de la habitación | ||
| - | <center><math>Q_\mathrm{out}=-Q = | + | <center><math>Q_\mathrm{out}=-Q = 6.47\,\mathrm{MJ}</math></center> |
| - | + | ||
| + | En una situación real, se trataría de un sistema abierto, con entrada o salida de aire, de manera que tanto la presión como el volumen permanecen constantes, pero hacemos un modelo más sencillo. | ||
| + | |||
==Variación de entropía== | ==Variación de entropía== | ||
| + | Para la variación de entropía de un gas ideal a volumen constante tenemos la fórmula | ||
| + | |||
| + | <center><math>\Delta S = n c_v\ln\left(\frac{T_f}{T_i}\right)</math></center> | ||
| + | |||
| + | que para este caso da | ||
| + | |||
| + | <center><math>\Delta S = 17300\times 20.785\times\ln\left(\frac{295}{313}\right)\,\frac{\mathrm{J}}{\mathrm{K}} = -21.3\,\frac{\mathrm{kJ}}{\mathrm{K}}</math></center> | ||
| + | |||
| + | La variación de entropía es negativa, como corresponde al enfriamiento de un gas. | ||
| + | |||
==Coeficiente de desempeño== | ==Coeficiente de desempeño== | ||
| + | El coeficiente de desempeño máximo lo da un refrigerador que funcione según un ciclo reversible y vale | ||
| + | |||
| + | <center><math>\mathrm{COP}_R = \frac{T_f}{T_c-T_f}=\frac{295}{18}=16.4</math></center> | ||
==Calor de desecho== | ==Calor de desecho== | ||
| + | Para un refrigerador (ideal o no) | ||
| + | |||
| + | <center><math>\mathrm{COP}_R=\frac{Q_\mathrm{in}}{W_\mathrm{in}}\qquad\Rightarrow\qquad W_\mathrm{in}=\frac{Q_\mathrm{in}}{\mathrm{COP}_R}</math></center> | ||
| + | |||
| + | que para este caso vale | ||
| + | |||
| + | <center><math>W_\mathrm{in} = \frac{6.47}{3.0}\,\mathrm{MJ} = 2.16\,\mathrm{MJ}</math></center> | ||
| + | |||
| + | El calor de desecho que se expulsa es la suma del que se absorbe y del trabajo realizado por la máquina | ||
| + | |||
| + | <center><math>Q_\mathrm{out}=Q_\mathrm{in}+W_\mathrm{in}= (6.47+2.16)\,\mathrm{MJ}=8.63\,\mathrm{MJ}</math></center> | ||
| + | |||
[[Categoría:Problemas de máquinas térmicas (GIE)]] | [[Categoría:Problemas de máquinas térmicas (GIE)]] | ||
última version al 19:20 8 sep 2012
Contenido |
1 Enunciado
En una habitación de 15 m×10 m×3 m hay aire (equivalente a un gas ideal diatómico de peso molecular 28.97 g/mol) a 40 °C (que también es la temperatura exterior) y 100 kPa.
- ¿Cuál es la masa de aire contenida en la habitación?
- Con un aparato de aire acondicionado se baja la temperatura de la habitación (con las ventanas y puertas cerradas) hasta 22 °C. ¿Cuánto calor sale de la habitación?
- ¿Cuánto varía la entropía del aire de la habitación en el proceso anterior?
- ¿Cuánto es el coeficiente de desempeño (COPR) máximo que puede tener un aparato de aire acondicionado que funcione entre las dos temperaturas indicadas?
- Si el COPR del aparato empleado es 3.0, ¿cuánto calor de desecho se expulsa al exterior?
2 Masa de aire
Para hallar la masa de aire aplicamos la ley de los gases ideales. Primero calculamos el volumen y la temperatura absoluta

luego el número de moles
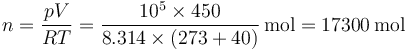
y, conociendo el peso molecular aparente, la masa de aire
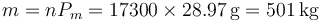
3 Calor extraído
Puesto que las puertas y ventanas están cerradas, se trata de un proceso a volumen constante, por el que el calor que entra en el sistema es
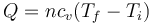
siendo
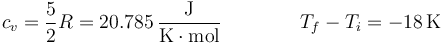
y el calor
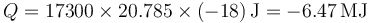
puesto que se nos pide el calor que sale de la habitación
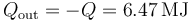
En una situación real, se trataría de un sistema abierto, con entrada o salida de aire, de manera que tanto la presión como el volumen permanecen constantes, pero hacemos un modelo más sencillo.
4 Variación de entropía
Para la variación de entropía de un gas ideal a volumen constante tenemos la fórmula
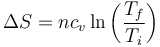
que para este caso da
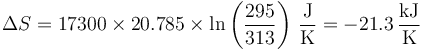
La variación de entropía es negativa, como corresponde al enfriamiento de un gas.
5 Coeficiente de desempeño
El coeficiente de desempeño máximo lo da un refrigerador que funcione según un ciclo reversible y vale
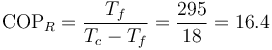
6 Calor de desecho
Para un refrigerador (ideal o no)
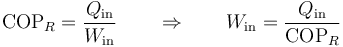
que para este caso vale
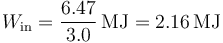
El calor de desecho que se expulsa es la suma del que se absorbe y del trabajo realizado por la máquina