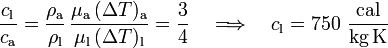Tubería calentada con flujo de líquido GIA
De Laplace
(→Solución) |
(→Solución) |
||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 5: | Línea 5: | ||
==Solución== | ==Solución== | ||
| - | El dato de que la llama es invariable debemos intepretarlo en el sentido de que, en intervalos iguales de tiempo, la llama suministra | + | El dato de que la llama es invariable debemos intepretarlo en el sentido de que, en intervalos iguales de tiempo, la llama suministra idénticas cantidades de calor. O lo que es lo mismo, la cantidad de calor que suministra por unidad de tiempo es un valor constante: |
[[Archivo:bol_T2_01_1.gif|right]]<center><math>\frac{\mathrm{d}Q}{\mathrm{d}t}=\frac{\Delta Q}{\Delta t}=\lambda\,\mathrm{,}\,\;\;\mathrm{cte.,}\;\;\forall\, \Delta t</math></center> | [[Archivo:bol_T2_01_1.gif|right]]<center><math>\frac{\mathrm{d}Q}{\mathrm{d}t}=\frac{\Delta Q}{\Delta t}=\lambda\,\mathrm{,}\,\;\;\mathrm{cte.,}\;\;\forall\, \Delta t</math></center> | ||
| Línea 11: | Línea 11: | ||
Por otra parte, tanto el agua como el líquido problema, fluyen por la tubería de manera que sus respectivos caudales son constantes; es decir, el volumen que por unidad de tiempo cruza la sección transversal de la tubería tiene un valor constante para cada uno de los fluidos. Y si éstos son incompresibles,la cantidad de masa de fluido líquido que en un intervalo de tiempo <math>\Delta t</math>, pasa de la zona fría a la caliente será: | Por otra parte, tanto el agua como el líquido problema, fluyen por la tubería de manera que sus respectivos caudales son constantes; es decir, el volumen que por unidad de tiempo cruza la sección transversal de la tubería tiene un valor constante para cada uno de los fluidos. Y si éstos son incompresibles,la cantidad de masa de fluido líquido que en un intervalo de tiempo <math>\Delta t</math>, pasa de la zona fría a la caliente será: | ||
| - | <center><math>\frac{\mathrm{d}V}{\mathrm{d}t}=\mu\,\mathrm{,}\,\; \; cte.\quad\Longrightarrow\quad \Delta m=\rho_m\!\ \mu\!\ \Delta t</math></center> | + | <center><math>\frac{\mathrm{d}V}{\mathrm{d}t}=\mu\,\mathrm{,}\,\; \; cte.\quad\Longrightarrow\quad \Delta m=\rho_m\ \frac{\mathrm{d}V}{\mathrm{d}t}\ \Delta t=\rho_m\!\ \mu\!\ \Delta t</math></center> |
siendo <math>\rho_m</math> la densidad de masa. Y si esta masa ha cambiado su temperatura desde un valor <math>T_1</math> a otro <math>T_2</math>, en el intervalo de tiempo <math>\Delta t</math> habrá absorbido una cantidad de calor, obviamente sumistrada por la llama invariable: | siendo <math>\rho_m</math> la densidad de masa. Y si esta masa ha cambiado su temperatura desde un valor <math>T_1</math> a otro <math>T_2</math>, en el intervalo de tiempo <math>\Delta t</math> habrá absorbido una cantidad de calor, obviamente sumistrada por la llama invariable: | ||
| Línea 21: | Línea 21: | ||
<center><math>\lambda=c_\mathrm{a} \rho_\mathrm{a}\mu_\mathrm{a}\!\ (\Delta T)_\mathrm{a}= c_\mathrm{l} \rho_\mathrm{l}\mu_\mathrm{l}\!\ (\Delta T)_\mathrm{l}</math></center> | <center><math>\lambda=c_\mathrm{a} \rho_\mathrm{a}\mu_\mathrm{a}\!\ (\Delta T)_\mathrm{a}= c_\mathrm{l} \rho_\mathrm{l}\mu_\mathrm{l}\!\ (\Delta T)_\mathrm{l}</math></center> | ||
| - | Para el caso del flujo de agua, | + | Para el caso del flujo de agua, el caudal es <math>\mu_\mathrm{a}=50\ \mathrm{l}/\mathrm{s}</math>, y el incremento de temperatura entre un extremo y otro es <math>(\Delta T)_\mathrm{a}=15\,\mathrm{K}</math>. Como datos del líquido problema tenemos que su caudal es <math>\mu_\mathrm{l}=25\ \mathrm{l}/\mathrm{s}</math>, que sufre un incremento de temperatura <math>(\Delta T)_\mathrm{l}=50\,\mathrm{K}</math>, y que su densidad es <math>0.8</math> veces las del agua. Con esto se obtiene: |
| - | <center><math>c_\mathrm{l} | + | <center><math>\frac{c_\mathrm{l}}{c_\mathrm{a}}= |
| - | \frac{\rho_\mathrm{a}}{\rho_\mathrm{l}}\!\ \frac{ \mu_\mathrm{a}\!\ (\Delta T)_\mathrm{a}}{\mu_\mathrm{l}\!\ (\Delta T)_\mathrm{l}}\ | + | \frac{\rho_\mathrm{a}}{\rho_\mathrm{l}}\!\ \frac{ \mu_\mathrm{a}\!\ (\Delta T)_\mathrm{a}}{\mu_\mathrm{l}\!\ (\Delta T)_\mathrm{l}}=\frac{3}{4}\quad\Longrightarrow\quad c_\mathrm{l}=750\ \frac{\mathrm{cal}}{\mathrm{kg}\, \mathrm{K}} </math></center> |
última version al 20:58 6 jun 2012
1 Enunciado
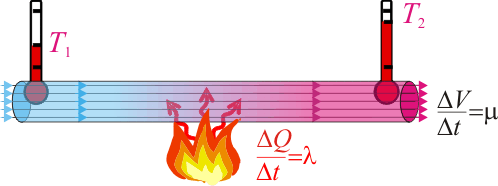
Por una tubería calentada en su punto medio con una llama invariable fluyen 50 l de agua por segundo. La temperatura de entrada es de 20 °C, y la de salida de 35 °C. Otro líquido de densidad 0.8, circula a continuación por el mismo tubo calentado por la misma llama, pero con un caudal de 25 l/s. Las temperaturas en los dos extremos se estacionan ahora en 18 °C y en 68 °C. Calcular el calor específico del líquido.
2 Solución
El dato de que la llama es invariable debemos intepretarlo en el sentido de que, en intervalos iguales de tiempo, la llama suministra idénticas cantidades de calor. O lo que es lo mismo, la cantidad de calor que suministra por unidad de tiempo es un valor constante:
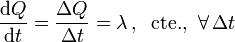
Por otra parte, tanto el agua como el líquido problema, fluyen por la tubería de manera que sus respectivos caudales son constantes; es decir, el volumen que por unidad de tiempo cruza la sección transversal de la tubería tiene un valor constante para cada uno de los fluidos. Y si éstos son incompresibles,la cantidad de masa de fluido líquido que en un intervalo de tiempo Δt, pasa de la zona fría a la caliente será:
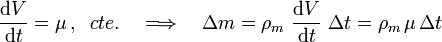
siendo ρm la densidad de masa. Y si esta masa ha cambiado su temperatura desde un valor T1 a otro T2, en el intervalo de tiempo Δt habrá absorbido una cantidad de calor, obviamente sumistrada por la llama invariable:
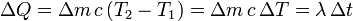
donde c es el correspondiente valor de calor específico. Obsérvese que los dos líquidos estudiados tienen caudales y calores específicos distintos y sufren distintos cambios en sus temperaturas, pero la llama es la misma en ambos casos; por tanto, se tendrá:
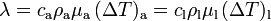
Para el caso del flujo de agua, el caudal es 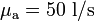 , y el incremento de temperatura entre un extremo y otro es
, y el incremento de temperatura entre un extremo y otro es 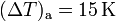 . Como datos del líquido problema tenemos que su caudal es
. Como datos del líquido problema tenemos que su caudal es 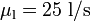 , que sufre un incremento de temperatura
, que sufre un incremento de temperatura 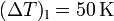 , y que su densidad es 0.8 veces las del agua. Con esto se obtiene:
, y que su densidad es 0.8 veces las del agua. Con esto se obtiene: