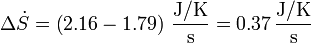Producción de entropía en un frigorífico
De Laplace
(Diferencias entre revisiones)
(→Solución) |
|||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 8: | Línea 8: | ||
:Puesto que el de este frigorífico real es un 25% del máximo | :Puesto que el de este frigorífico real es un 25% del máximo | ||
| - | <center><math>\mathrm{COP}_R = 0.25\times 13.1 = 3.29</math></center> | + | <center><math>\mathrm{COP}_R = 0.25\times 13.1 = 3.29\,</math></center> |
;Calor extraído: Una vez que tenemos el coeficiente de desempeño hallamos el calor extraído en la unidad de tiempo | ;Calor extraído: Una vez que tenemos el coeficiente de desempeño hallamos el calor extraído en la unidad de tiempo | ||
| Línea 20: | Línea 20: | ||
;Producción de entropía: Cada segundo el refrigerador extrae una entropía del foco frío | ;Producción de entropía: Cada segundo el refrigerador extrae una entropía del foco frío | ||
| - | <center><math>\Delta \dot{S}_F = \frac{\dot{Q}_\mathrm{in}{T_F}= \frac{493}{276}\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}} = | + | <center><math>\Delta \dot{S}_F = -\frac{\dot{Q}_\mathrm{in}}{T_F}= -\frac{493}{276}\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}} = -1.79\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}</math></center> |
:y cede una entropía al foco caliente | :y cede una entropía al foco caliente | ||
| - | <center><math>\Delta \dot{S}_C = \frac{\dot{Q}_\mathrm{out}{T_C}= \frac{643}{297}\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}} = +2.16\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}</math></center> | + | <center><math>\Delta \dot{S}_C = \frac{\dot{Q}_\mathrm{out}}{T_C}= \frac{643}{297}\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}} = +2.16\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}</math></center> |
: La entropía del refrigerador no cambia, por operar cíclicamente. Por tanto, la variación de entropía del universo por segundo es | : La entropía del refrigerador no cambia, por operar cíclicamente. Por tanto, la variación de entropía del universo por segundo es | ||
| - | <center><math>\Delta \dot{S}=\left(2.16-1.79)\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}= 0.37\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}</math></center> | + | <center><math>\Delta \dot{S}=\left(2.16-1.79\right)\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}= 0.37\,\frac{\mathrm{J}/\mathrm{K}}{\mathrm{s}}</math></center> |
[[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | [[Categoría:Problemas del segundo principio de la termodinámica (GIE)]] | ||
última version al 09:16 18 mar 2014
1 Enunciado
Un frigorífico doméstico mantiene su interior a 3°C, estando la cocina a 24°C, siendo su un coeficiente de desempeño del 25% respecto al máximo y consumiendo una potencia de 150 W. Determine la cantidad de calor extraído por segundo, el calor arrojado al ambiente y la entropía producida por segundo.
2 Solución
- Coeficiente de desempeño
- El valor máximo del coeficiente de desempeño lo da un refrigerador reversible
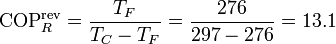
- Puesto que el de este frigorífico real es un 25% del máximo

- Calor extraído
- Una vez que tenemos el coeficiente de desempeño hallamos el calor extraído en la unidad de tiempo
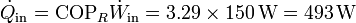
- Calor desechado
- El calor expulsado a la habitación es la suma del extraído y del trabajo realizado. Lo mismo para el flujo de calor
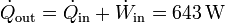
- Producción de entropía
- Cada segundo el refrigerador extrae una entropía del foco frío
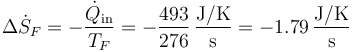
- y cede una entropía al foco caliente
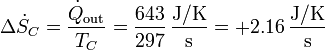
- La entropía del refrigerador no cambia, por operar cíclicamente. Por tanto, la variación de entropía del universo por segundo es