Tubo con dos cámaras de gas
De Laplace
(→Solución sin emplear el número de moles) |
|||
| (6 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
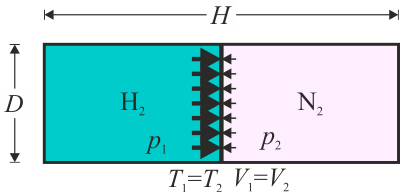
| - | Se tiene una cámara cilíndrica horizontal de 20 cm de diámetro y 60 cm de longitud de paredes rígidas. En el punto medio del tubo se encuentra un émbolo (de espesor despreciable) que puede desplazarse, aunque inicialmente | + | Se tiene una cámara cilíndrica horizontal de 20 cm de diámetro y 60 cm de longitud de paredes rígidas no aisladas térmicamente. En el punto medio del tubo se encuentra un émbolo (de espesor despreciable) que puede desplazarse, aunque inicialmente está fijado con pernos. En la cámara de la izquierda hay 4.0 g de H<sub>2</sub> gaseoso y en la de la derecha 4.0 g de N<sub>2</sub>. Los dos gases y el ambiente que los rodea están a 25°C. |
| - | está fijado con pernos. En la cámara de la izquierda hay 4.0 g de H<sub>2</sub> gaseoso y en la de la derecha 4.0 g de N<sub>2</sub>. Los dos gases y el ambiente que los rodea están a 25°C. | + | |
# Halle la fuerza que los gases producen sobre el émbolo cuando éste se encuentra en la posición central. | # Halle la fuerza que los gases producen sobre el émbolo cuando éste se encuentra en la posición central. | ||
# Determine la posición final del émbolo una vez que se liberan los pernos, suponiendo que todas las superficies son diatermas | # Determine la posición final del émbolo una vez que se liberan los pernos, suponiendo que todas las superficies son diatermas | ||
| + | |||
==Fuerza== | ==Fuerza== | ||
Sea <math>H = 60\,\mathrm{cm}</math> la longitud del tubo y | Sea <math>H = 60\,\mathrm{cm}</math> la longitud del tubo y | ||
| Línea 29: | Línea 29: | ||
Esto nos da la presión del hidrógeno | Esto nos da la presión del hidrógeno | ||
| - | <center><math>p_1 = \frac{n_1 R T_1}{V_1}= \frac{1.984\times 8.314\times 298.15}{9.425\times 10^{-3}}\,\mathrm{Pa} = 522000\,\mathrm{Pa} = 5. | + | <center><math>p_1 = \frac{n_1 R T_1}{V_1}= \frac{1.984\times 8.314\times 298.15}{9.425\times 10^{-3}}\,\mathrm{Pa} = 522000\,\mathrm{Pa} = 5.22\,\mathrm{bar}</math></center> |
y la del nitrógeno | y la del nitrógeno | ||
| Línea 36: | Línea 36: | ||
Obsérvese que al emplear todas las cantidades en el SI, ya el resultado queda directamente en pascales (o en un múltiplo como el bar), no siendo preciso el usar las atmósferas para hacer los cálculos. | Obsérvese que al emplear todas las cantidades en el SI, ya el resultado queda directamente en pascales (o en un múltiplo como el bar), no siendo preciso el usar las atmósferas para hacer los cálculos. | ||
| + | |||
| + | [[Archivo:dos-camaras-01.png|right]] | ||
Vemos que la presión es mucho mayor en el lado del hidrógeno, por haber muchos más moles de este gas. | Vemos que la presión es mucho mayor en el lado del hidrógeno, por haber muchos más moles de este gas. | ||
| Línea 43: | Línea 45: | ||
<center><math>F = (p_1-p_2)S = (522000-37600)\times 0.314\,\mathrm{N} = 15.2\,\mathrm{kN}</math></center> | <center><math>F = (p_1-p_2)S = (522000-37600)\times 0.314\,\mathrm{N} = 15.2\,\mathrm{kN}</math></center> | ||
| - | Resulta una fuerza gigantesca, debida a la elevada diferencia de presiones entre los dos lados. | + | Resulta una fuerza gigantesca, debida a la elevada diferencia de presiones entre los dos lados. Esta fuerza va dirigida desde el lado del hidrógeno, que está a mayor presión, hacia el del nitrógeno, donde es más reducida. |
==Posición de equilibrio== | ==Posición de equilibrio== | ||
| + | [[Archivo:dos-camaras-02.png|right]] | ||
| + | |||
| + | Si liberamos el pistón, este saldrá disparado (ya que se trata, en el fondo, de una pistola de aire comprimido), pero –suponiendo que no se rompa–, al expandirse el hidrógeno, se comprime el nitrógeno, con lo que la presión de uno disminuye y la del otro aumenta. Cuando se alcanza de nuevo el equilibrio mecánico, las dos presiones son iguales, aunque no sabemos cuanto vale, por ahora, | ||
| + | |||
| + | <center><math>p_1 = p_2\,</math></center> | ||
| + | |||
| + | y, puesto que el sistema tiene paredes diatermas, la temperatura de los dos gases será la misma e igual a la exterior | ||
| + | |||
| + | <center><math>T_1 = T_2 = 298.15\,\mathrm{K}</math></center> | ||
| + | |||
| + | Tampoco conocemos el volumen de cada gas, pero sí que juntos nos dan el volumen total. Si <math>h_1</math> y <math>h_2</math> son las longitudes de cada cámara en la dirección del eje del cilindro | ||
| + | |||
| + | <center><math>h_1 + h_2 = H\qquad\qquad V_1 = h_1S\qquad\qquad V_2 = h_2S</math></center> | ||
| + | |||
| + | Nos queda entonces el sistema de ecuaciones | ||
| + | |||
| + | <center><math>h_1+h_2 = H\qquad\qquad \frac{n_1RT_1}{Sh_1}=\frac{n_2RT_2}{Sh_2}\qquad\Rightarrow\qquad \frac{n_1}{h_1}=\frac{n_2}{h_2}</math></center> | ||
| + | |||
| + | con la solución | ||
| + | |||
| + | <center><math>h_1 = \frac{n_1H}{n_1+n_2}=56.0\,\mathrm{cm}\qquad\qquad h_2 = \frac{n_2H}{n_1+n_2}=4.0\,\mathrm{cm}</math></center> | ||
| + | |||
| + | Vemos que el hidrógeno se expande hasta ocupar casi todo el cilindro. | ||
| + | |||
| + | ==Solución sin emplear el número de moles== | ||
| + | Este problema puede resolverse sin hallar previamente el número de moles, empleando simplemente la ley de los gases ideales. | ||
| + | |||
| + | Tenemos que inicialmente cada gas ocupa un volumen <math>V_0/2= SL/2</math> y está a una temperatura <math>T_0</math> (constante en todo momento). | ||
| + | |||
| + | Una vez que el pistón se mueve, las dos presiones son iguales a una presión final <math>p_f</math>, pero el volumen que ocupa cada gas no. La ley de los gases ideales nos da | ||
| + | |||
| + | <center><math>\begin{array}{rcl} | ||
| + | p_fV_1 & = & \dfrac{m}{P_{m1}}RT \\ && \\ p_fV_2 & = & \dfrac{m}{P_{m2}}RT | ||
| + | \end{array}</math></center> | ||
| + | |||
| + | Si sumamos estas dos ecuaciones y aplicamos que <math>V_1+V_2 = V_0</math> queda | ||
| + | |||
| + | <center><math>p_f V_0 = \left(\frac{m}{P_{m1}}+ \frac{m}{P_{m1}} \right)RT = \frac{m(P_{m1}+P_{m2})RT}{P_{m1}P_{m2}}</math></center> | ||
| + | |||
| + | (aquí se ha usado que las dos masas son iguales; si son diferentes habrá que indicar <math>m_1</math> y <math>m_2</math>, pero la lógica de la solución es la misma). De aquí obtenemos la presión final | ||
| + | |||
| + | <center><math>p_f = \frac{m(P_{m1}+P_{m2})RT}{P_{m1}P_{m2}V_0}</math></center> | ||
| + | |||
| + | y llevando esto a la ecuación para cada gas calculamos el volumen que ocupa | ||
| + | |||
| + | <center><math>V_1 = \frac{mRT}{P_{m1}p_f}=\frac{P_{m2}}{P_{m1}+P_{m2}}V_0\qquad\qquad V_2 = \frac{P_{m1}}{P_{m1}+P_{m2}}V_0</math></center> | ||
| + | |||
| + | es decir, el volumen ocupado por cada gas solo depende inversamente de la relación entre sus pesos moleculares | ||
| + | |||
| + | <center><math>\frac{V_1}{V_2}=\frac{P_{m2}}{P_{m1}}</math></center> | ||
| + | |||
| + | Puesto que el peso molecular del nitrógeno es 14 veces el del hidrógeno, esto hace que el nitrógeno ocupe un volumen 14 veces menor. | ||
| + | |||
| + | <center><math>h_1 =\frac{28}{28+2}60\,\mathrm{cm}=56\,\mathrm{cm}\qquad\qquad h_2 = 4\,\mathrm{cm}</math></center> | ||
| + | |||
| + | |||
| + | |||
[[Categoría:Problemas de introducción a la termodinámica (GIE)]] | [[Categoría:Problemas de introducción a la termodinámica (GIE)]] | ||
última version al 10:59 1 abr 2015
Contenido |
1 Enunciado
Se tiene una cámara cilíndrica horizontal de 20 cm de diámetro y 60 cm de longitud de paredes rígidas no aisladas térmicamente. En el punto medio del tubo se encuentra un émbolo (de espesor despreciable) que puede desplazarse, aunque inicialmente está fijado con pernos. En la cámara de la izquierda hay 4.0 g de H2 gaseoso y en la de la derecha 4.0 g de N2. Los dos gases y el ambiente que los rodea están a 25°C.
- Halle la fuerza que los gases producen sobre el émbolo cuando éste se encuentra en la posición central.
- Determine la posición final del émbolo una vez que se liberan los pernos, suponiendo que todas las superficies son diatermas
2 Fuerza
Sea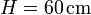 
la longitud del tubo y
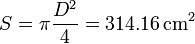
su sección. El volumen cada gas es el mismo, la mitad del del cilindro
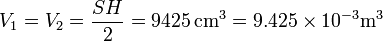
y también son iguales sus temperaturas
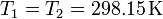
Sus presiones, sin embargo, son diferentes. Aunque en las dos cámaras se encuentra la misma masa de gas, el número de moles es diferente. Obtenemos la cantidad de moles dividiendo por el peso molecular. Para el hidrógeno
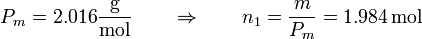
y para el nitrógeno
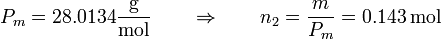
En estas fórmulas se podían haber usado como masas moleculares 2 g/mol y 28 g/mol, y el resultado sería bastante aproximado al correcto.
Esto nos da la presión del hidrógeno
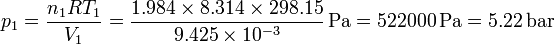
y la del nitrógeno
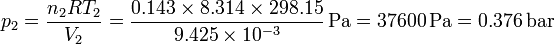
Obsérvese que al emplear todas las cantidades en el SI, ya el resultado queda directamente en pascales (o en un múltiplo como el bar), no siendo preciso el usar las atmósferas para hacer los cálculos.
Vemos que la presión es mucho mayor en el lado del hidrógeno, por haber muchos más moles de este gas.
La fuerza sobre el émbolo la obtenemos a partir de la diferencia de presiones
Resulta una fuerza gigantesca, debida a la elevada diferencia de presiones entre los dos lados. Esta fuerza va dirigida desde el lado del hidrógeno, que está a mayor presión, hacia el del nitrógeno, donde es más reducida.
3 Posición de equilibrio
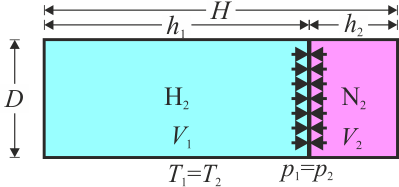
Si liberamos el pistón, este saldrá disparado (ya que se trata, en el fondo, de una pistola de aire comprimido), pero –suponiendo que no se rompa–, al expandirse el hidrógeno, se comprime el nitrógeno, con lo que la presión de uno disminuye y la del otro aumenta. Cuando se alcanza de nuevo el equilibrio mecánico, las dos presiones son iguales, aunque no sabemos cuanto vale, por ahora,
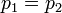
y, puesto que el sistema tiene paredes diatermas, la temperatura de los dos gases será la misma e igual a la exterior
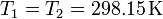
Tampoco conocemos el volumen de cada gas, pero sí que juntos nos dan el volumen total. Si h1 y h2 son las longitudes de cada cámara en la dirección del eje del cilindro
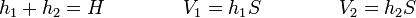
Nos queda entonces el sistema de ecuaciones
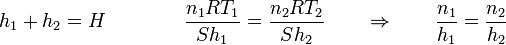
con la solución
Vemos que el hidrógeno se expande hasta ocupar casi todo el cilindro.
4 Solución sin emplear el número de moles
Este problema puede resolverse sin hallar previamente el número de moles, empleando simplemente la ley de los gases ideales.
Tenemos que inicialmente cada gas ocupa un volumen V0 / 2 = SL / 2 y está a una temperatura T0 (constante en todo momento).
Una vez que el pistón se mueve, las dos presiones son iguales a una presión final pf, pero el volumen que ocupa cada gas no. La ley de los gases ideales nos da
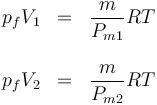
Si sumamos estas dos ecuaciones y aplicamos que V1 + V2 = V0 queda
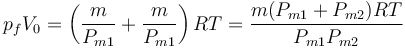
(aquí se ha usado que las dos masas son iguales; si son diferentes habrá que indicar m1 y m2, pero la lógica de la solución es la misma). De aquí obtenemos la presión final
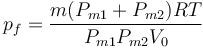
y llevando esto a la ecuación para cada gas calculamos el volumen que ocupa
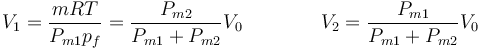
es decir, el volumen ocupado por cada gas solo depende inversamente de la relación entre sus pesos moleculares
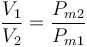
Puesto que el peso molecular del nitrógeno es 14 veces el del hidrógeno, esto hace que el nitrógeno ocupe un volumen 14 veces menor.
