Colisión entre dos masas desiguales
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Solución) |
||
| Línea 14: | Línea 14: | ||
<center><math>\vec{v}_{2f}=\frac{m(8v_0\vec{\imath})-m(2v_0\vec{\imath}+2v_0\vec{\jmath})}{2m}= \frac{6v_0\vec{\imath}-2v_0\vec{\jmath}}{2}=v_0\left(3\vec{\imath}-\vec{\jmath}\right)</math></center> | <center><math>\vec{v}_{2f}=\frac{m(8v_0\vec{\imath})-m(2v_0\vec{\imath}+2v_0\vec{\jmath})}{2m}= \frac{6v_0\vec{\imath}-2v_0\vec{\jmath}}{2}=v_0\left(3\vec{\imath}-\vec{\jmath}\right)</math></center> | ||
| + | |||
<center>[[Archivo:colision-masas-desiguales.png]]</center> | <center>[[Archivo:colision-masas-desiguales.png]]</center> | ||
[[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | [[Categoría:Problemas de dinámica de los sistemas de partículas (GIE)]] | ||
última version al 11:34 21 ene 2012
1 Enunciado
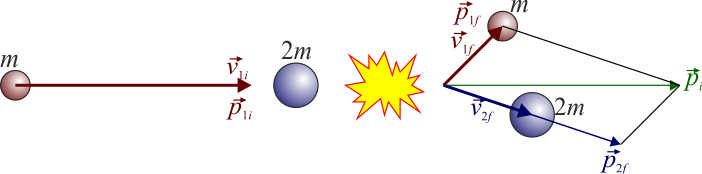
Una proyectil de masa m que se mueve con velocidad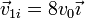 
colisiona con un blanco inmóvil de masa 2m. El proyectil tiene tras la colisión una velocidad 
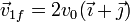¿Cuánto vale la velocidad final de la segunda masa?
2 Solución
En una colisión, elástica o inelástica, todas las fuerzas son internas, por lo que se conserva la cantidad de movimiento del sistema. Por tanto, para hallar la velocidad final de la segunda masa nos basta con igualar la cantidad de movimiento inicial a la final
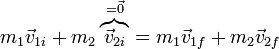
Despejando
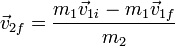
y sustituyendo
