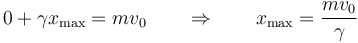Amortiguamiento viscoso
De Laplace
| (Una edición intermedia no se muestra.) | |||
| Línea 29: | Línea 29: | ||
<center><math>\ln\left(\frac{v}{v_0}\right) = -\frac{\gamma}{m} t\qquad\Rightarrow\qquad v = v_0\mathrm{e}^{-\gamma t/m}</math></center> | <center><math>\ln\left(\frac{v}{v_0}\right) = -\frac{\gamma}{m} t\qquad\Rightarrow\qquad v = v_0\mathrm{e}^{-\gamma t/m}</math></center> | ||
| - | Vemos que la velocidad decae exponencialmente y (teóricamente), nunca llega a pararse. Ello no quiere decir que la distancia recorrida sea infinita. Integrando de nuevo tenemos | + | [[Archivo:decaimiento-exponencial.png|right]] |
| + | |||
| + | Vemos que la velocidad decae exponencialmente y (teóricamente), nunca llega a pararse. Ello no quiere decir que la distancia recorrida sea infinita, ya que el área bajo la curva es finita. Integrando de nuevo tenemos | ||
<center><math>\frac{\mathrm{d}x}{\mathrm{d}t}=v = v_0\mathrm{e}^{-\gamma t/m}\qquad\Rightarrow\qquad x = \int_0^t v_0\mathrm{e}^{-\gamma t/m}\mathrm{d}t=\frac{mv_0}{\gamma}\left(1-\mathrm{e}^{-\gamma t/m}\right)</math></center> | <center><math>\frac{\mathrm{d}x}{\mathrm{d}t}=v = v_0\mathrm{e}^{-\gamma t/m}\qquad\Rightarrow\qquad x = \int_0^t v_0\mathrm{e}^{-\gamma t/m}\mathrm{d}t=\frac{mv_0}{\gamma}\left(1-\mathrm{e}^{-\gamma t/m}\right)</math></center> | ||
| Línea 42: | Línea 44: | ||
<center><math>v_0 = \frac{\gamma\,\Delta x}{m}</math></center> | <center><math>v_0 = \frac{\gamma\,\Delta x}{m}</math></center> | ||
| + | |||
| + | ==Solución alternativa== | ||
| + | Este problema puede resolverse de manera alternativa, con ayuda de las constantes de movimiento. | ||
| + | |||
| + | La velocidad es la derivada de la posición respecto al tiempo. Por tanto, la ecuación de movimiento puede escribirse como | ||
| + | |||
| + | <center><math>m\frac{\mathrm{d}v}{\mathrm{d}t}=-\gamma\frac{\mathrm{d}x}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | o lo que es lo mismo | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}\ }{\mathrm{d}t}\left(mv+\gamma x\right)=0</math></center> | ||
| + | |||
| + | Puesto que la derivada se anula, lo que hay dentro del paréntesis debe ser una constante de movimiento | ||
| + | |||
| + | <center><math>mv+\gamma x = \mathrm{cte} = mv_0\,</math></center> | ||
| + | |||
| + | El valor de la constante ha salido de su valor en <math>t=0</math>. | ||
| + | |||
| + | La partícula se para cuando <math>v=0</math>, lo que nos da | ||
| + | |||
| + | <center><math>0+\gamma x_\mathrm{max}=mv_0\qquad\Rightarrow\qquad x_\mathrm{max}=\frac{mv_0}{\gamma}</math></center> | ||
| + | |||
[[Categoría:Problemas de dinámica de la partícula (GIE)]] | [[Categoría:Problemas de dinámica de la partícula (GIE)]] | ||
última version al 12:40 27 nov 2014
1 Enunciado
El rozamiento que experimenta una pequeña partícula en medio denso y viscoso como un aceite es de la forma 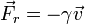 . Se construye un sensor de balística, en el que una bala de masa m impacta horizontalmente en un bloque de silicona en el que se cumple la ley anterior. Si la bala recorre una distancia x0 hasta pararse. ¿Con qué velocidad impactó en el bloque?
. Se construye un sensor de balística, en el que una bala de masa m impacta horizontalmente en un bloque de silicona en el que se cumple la ley anterior. Si la bala recorre una distancia x0 hasta pararse. ¿Con qué velocidad impactó en el bloque?
2 Solución
La bala, una vez que penetra en la silicona, se ve frenada. Inicialmente entra con una velocidad  , que suponemos horizontal, y la fuerza de rozamiento va reduciendo su rapidez, hasta que llega a detenerse por completo. Hasta que se para recorre una cierta distancia Δx. Se trata de calcular esta distancia y relacionarla con la velocidad inicial.
, que suponemos horizontal, y la fuerza de rozamiento va reduciendo su rapidez, hasta que llega a detenerse por completo. Hasta que se para recorre una cierta distancia Δx. Se trata de calcular esta distancia y relacionarla con la velocidad inicial.
Lu ecuación de movimiento de la bala se reduce a
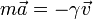
con las condiciones iniciales

Despreciando el efecto del peso, podemos suponer que el movimiento es horizontal en todo instante, lo cual nos permite emplear cantidades escalares
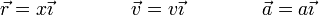
lo cual nos deja con las ecuaciones escalares
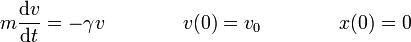
La solución de esta ecuación diferencial es elemental, ya que podemos separarla en dos integrales
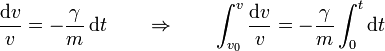
siendo el resultado
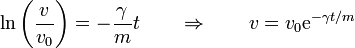
Vemos que la velocidad decae exponencialmente y (teóricamente), nunca llega a pararse. Ello no quiere decir que la distancia recorrida sea infinita, ya que el área bajo la curva es finita. Integrando de nuevo tenemos
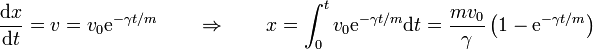
Esta integral se va acercando asintóticamente a un valor constante.
Cuando 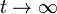 la velocidad de la bala se anula y la distancia total que recorre es
la velocidad de la bala se anula y la distancia total que recorre es

y, por tanto, si lo que medimos es la distancia total recorrida, hallamos la velocidad de entrada despejando

3 Solución alternativa
Este problema puede resolverse de manera alternativa, con ayuda de las constantes de movimiento.
La velocidad es la derivada de la posición respecto al tiempo. Por tanto, la ecuación de movimiento puede escribirse como
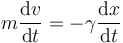
o lo que es lo mismo
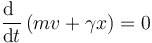
Puesto que la derivada se anula, lo que hay dentro del paréntesis debe ser una constante de movimiento
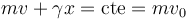
El valor de la constante ha salido de su valor en t = 0.
La partícula se para cuando v = 0, lo que nos da