Fuerza entre un dipolo y una espira
De Laplace
(Página creada con '==Enunciado== Se tiene un pequeño imán, modelable como un dipolo magnético puntual de momento magnético <math>\mathbf{m}_0=m_0\,\mathbf{u}_{z}</math>, situado a una cierta a…') |
|||
| (13 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Se tiene un pequeño imán, modelable como un dipolo magnético puntual de momento magnético <math>\mathbf{m}_0=m_0\,\mathbf{u}_{z}</math>, situado a una cierta altura <math> | + | Se tiene un pequeño imán, modelable como un dipolo magnético puntual de momento magnético <math>\mathbf{m}_0=m_0\,\mathbf{u}_{z}</math>, situado a una cierta altura <math>z_0</math> sobre el eje de una espira circular de radio <math>a</math> por la que circula una corriente eléctrica continua de intensidad <math>I_0</math>. |
Calcule la fuerza que la espira ejerce sobre el dipolo, y la que el dipolo produce sobre la espira. ¿Se verifica la tercera ley de Newton? | Calcule la fuerza que la espira ejerce sobre el dipolo, y la que el dipolo produce sobre la espira. ¿Se verifica la tercera ley de Newton? | ||
==De la espira sobre el dipolo== | ==De la espira sobre el dipolo== | ||
| + | La fuerza sobre el dipolo magnético puede calcularse como | ||
| + | |||
| + | <center><math>\mathbf{F}_\mathrm{I\to m}=\left.(\mathbf{m}\cdot\nabla)\mathbf{B}_I\right|_{z=z_0}</math></center> | ||
| + | |||
| + | siendo el primer factor el operador escalar | ||
| + | |||
| + | <center><math>\mathbf{m}\cdot\nabla = m\frac{\partial\ }{\partial z}</math></center> | ||
| + | |||
| + | Por tanto, necesitamos hallar la derivada, con respecto a la coordenada z, del campo magnético de la espira en los puntos del eje Z. Podemos calcular esta cantidad porque conocemos este campo para todo z: | ||
| + | |||
| + | <center><math>\mathbf{B}_\mathrm{esp}(z)=\frac{\mu_0I_0 a^2\mathbf{u}_z}{2(a^2+z^2)^{3/2}}</math></center> | ||
| + | |||
| + | Si hubiéramos tenido que hallar la derivada respecto a x o a y no habríamos podido calcularla, pues eso requeriría conocer el campo en puntos que no son del eje. | ||
| + | |||
| + | Aplicando el operador al campo | ||
| + | |||
| + | <center><math>\mathbf{F}_\mathrm{I\to m}=\left.m\frac{\partial\ }{\partial z}\left(\frac{\mu_0I_0 a^2\mathbf{u}_z}{2(a^2+z^2)^{3/2}}\right)\right|_{z=z_0} = -\frac{3\mu_0I_0ma^2z_0\mathbf{u}_z}{2(a^2+z_0^2)^{5/2}}</math></center> | ||
| + | |||
| + | Esta fuerza es nula justo en el centro de la espira y apunta hacia abajo si el dipolo se encuentra encima de la espira y hacia arriba si está por debajo. | ||
| + | |||
| + | <center>[[Archivo:fuerza-espira-dipolo.png|450px]]</center> | ||
| + | |||
| + | El sentido de la fuerza puede entenderse considerando que la espira se comporta como un dipolo cuyo polo norte está en su cara superior y el sur en la inferior, de forma que tanto por arriba como por abajo, tenemos la atracción entre polos opuestos. | ||
| + | |||
==Del dipolo sobre la espira== | ==Del dipolo sobre la espira== | ||
| + | La fuerza creada por el dipolo sobre la espira la hallamos mediante la fórmula para la fuerza sobre una corriente | ||
| + | |||
| + | <center><math>\mathbf{F}_{m\to I}=I_0\oint \mathrm{d}\mathbf{r}\times\mathbf{B}_m</math></center> | ||
| + | |||
| + | donde <math>\mathbf{B}_m</math> es el campo producido por el dipolo. Para usar la expresión más simple posible, suponemos el origen de coordenadas en la posición del dipolo, de forma que la espira se encuentra <math>z = -z_0</math>. | ||
| + | |||
| + | El campo entonces es | ||
| + | |||
| + | <center><math>\mathbf{M}=\frac{\mu_0}{4\pi}\,\frac{3((\mathbf{m}\cdot\mathbf{r})\mathbf{r}-r^2\mathbf{m}}{r^5}</math></center> | ||
| + | |||
| + | Este campo hay que evaluarlo en los puntos en que se encuentra la espira. Usando coordenadas cilíndricas | ||
| + | |||
| + | <center><math>\mathbf{r} = a\mathbf{u}_\rho - z_0\mathbf{u}_z</math></center> | ||
| + | |||
| + | siendo el módulo | ||
| + | |||
| + | <center><math>r = |\mathbf{r}| = \sqrt{a^2+z_0^2}</math></center> | ||
| + | |||
| + | lo que nos da | ||
| + | |||
| + | <center><math>\mathbf{B}=\frac{\mu_0m}{4\pi(a^2+z^2)^{5/2}}\left(3(-z_0)(a\mathbf{u}_\rho - z_0\mathbf{u}_z) - (a^2+z_0^2)\mathbf{u}_z\right)</math></center> | ||
| + | |||
| + | y | ||
| + | |||
| + | <center><math>\mathrm{d}\mathbf{r} = a\,\mathrm{d}\varphi\,\mathbf{u}_\varphi</math></center> | ||
| + | |||
| + | Al sustituir nos queda un integrando con una componente en la dirección de <math>\mathbf{u}_\rho</math> y otro en la de <math>\mathbf{u}_z</math>. La primera se anula sobre una circunferencia y queda solamente | ||
| + | |||
| + | <center><math>\mathbf{F}_{m\to I}= \frac{\mu_0mI_0}{4\pi}\int_0^{2\pi}\frac{3(-z_0)a}{(a^2+z_0^2)^{5/2}}(a\,\mathrm{d}\varphi) (-\mathbf{u}_z) = \frac{3\mu_0mI_0 a^2z_0}{2(z_0^2+a^2)^{5/2}}</math></center> | ||
| + | |||
| + | <center>[[Archivo:fuerza-dipolo-espira.png|450px]]</center> | ||
| + | |||
| + | Esta fuerza es igual en módulo y dirección y sentido opuesto al de la anterior. por tanto, se verifica la tercera ley de Newton. | ||
| + | |||
[[Categoría:Problemas de campo magnético de corrientes estacionarias]] | [[Categoría:Problemas de campo magnético de corrientes estacionarias]] | ||
última version al 16:29 30 may 2011
1 Enunciado
Se tiene un pequeño imán, modelable como un dipolo magnético puntual de momento magnético 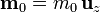 , situado a una cierta altura z0 sobre el eje de una espira circular de radio a por la que circula una corriente eléctrica continua de intensidad I0.
, situado a una cierta altura z0 sobre el eje de una espira circular de radio a por la que circula una corriente eléctrica continua de intensidad I0.
Calcule la fuerza que la espira ejerce sobre el dipolo, y la que el dipolo produce sobre la espira. ¿Se verifica la tercera ley de Newton?
2 De la espira sobre el dipolo
La fuerza sobre el dipolo magnético puede calcularse como

siendo el primer factor el operador escalar

Por tanto, necesitamos hallar la derivada, con respecto a la coordenada z, del campo magnético de la espira en los puntos del eje Z. Podemos calcular esta cantidad porque conocemos este campo para todo z:

Si hubiéramos tenido que hallar la derivada respecto a x o a y no habríamos podido calcularla, pues eso requeriría conocer el campo en puntos que no son del eje.
Aplicando el operador al campo

Esta fuerza es nula justo en el centro de la espira y apunta hacia abajo si el dipolo se encuentra encima de la espira y hacia arriba si está por debajo.

El sentido de la fuerza puede entenderse considerando que la espira se comporta como un dipolo cuyo polo norte está en su cara superior y el sur en la inferior, de forma que tanto por arriba como por abajo, tenemos la atracción entre polos opuestos.
3 Del dipolo sobre la espira
La fuerza creada por el dipolo sobre la espira la hallamos mediante la fórmula para la fuerza sobre una corriente

donde  es el campo producido por el dipolo. Para usar la expresión más simple posible, suponemos el origen de coordenadas en la posición del dipolo, de forma que la espira se encuentra z = − z0.
es el campo producido por el dipolo. Para usar la expresión más simple posible, suponemos el origen de coordenadas en la posición del dipolo, de forma que la espira se encuentra z = − z0.
El campo entonces es

Este campo hay que evaluarlo en los puntos en que se encuentra la espira. Usando coordenadas cilíndricas

siendo el módulo

lo que nos da

y

Al sustituir nos queda un integrando con una componente en la dirección de 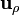 y otro en la de
y otro en la de  . La primera se anula sobre una circunferencia y queda solamente
. La primera se anula sobre una circunferencia y queda solamente


Esta fuerza es igual en módulo y dirección y sentido opuesto al de la anterior. por tanto, se verifica la tercera ley de Newton.





