5.10. Hélice de avión en rotación
De Laplace
(→Movimiento de arrastre {01}) |
m (6.10. Hélice de avión en rotación trasladada a 5.10. Hélice de avión en rotación) |
||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | El avión (sólido “0”) de la figura | + | El avión (sólido “0”) de la figura rota alrededor del eje vertical OZ<math>_1</math> de modo que el centro C de su hélice describe una circunferencia de radio <math>L</math> en el sistema de referencia fijo OX<math>_1</math>Y<math>_1</math>Z<math>_1</math> (sólido “1”). La velocidad angular de esta rotación es constante, su módulo es <math>|\vec{\omega}_{01}| = \Omega</math> y su sentido el indicado en la figura. Además, la hélice (sólido “2”), cuyo radio es <math>R</math>, rota en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad angular también de módulo constante <math>|\vec{\omega}_{20}| = \omega</math> y con el sentido indicado en la figura. Se pide |
# La reducción cinemática de los movimientos {01} y {20}. | # La reducción cinemática de los movimientos {01} y {20}. | ||
| - | # Aplicando | + | # Aplicando las leyes de composición de velocidades y aceleraciones, la velocidad <math>\vec{v}^P_{21}</math> y la aceleración <math>\vec{a}^P_{21}</math> del punto más alto de la hélice (punto P en la figura). |
| - | # La reducción cinemática del movimiento {21} en P y la ecuación de su EIRMD | + | # La reducción cinemática del movimiento {21} en P y la ecuación de su EIRMD ¿Qué tipo de movimiento describe la hélice respecto al sólido “1”? |
| - | # Calcule numéricamente <math>v^P_{21}</math> y <math>a^P_{21}</math> para los valores <math>R = 1\,\mathrm{m}</math>, <math>L | + | # Calcule numéricamente <math>\vec{v}^P_{21}</math> y <math>\vec{a}^P_{21}</math> para los valores <math>R = 1\,\mathrm{m}</math>, <math>L |
= 100\,\mathrm{m}</math>, <math>\omega = 100\,\mathrm{rad}/\mathrm{s}</math> y <math>\Omega = 1\,\mathrm{rad}/\mathrm{s}</math>. | = 100\,\mathrm{m}</math>, <math>\omega = 100\,\mathrm{rad}/\mathrm{s}</math> y <math>\Omega = 1\,\mathrm{rad}/\mathrm{s}</math>. | ||
<center>[[Archivo:helice-avion-rotacion.png]]</center> | <center>[[Archivo:helice-avion-rotacion.png]]</center> | ||
| - | '''Nota''': Se recomienda | + | '''Nota''': Se recomienda el uso de la base vectorial asociada al triedro “0” para resolver el ejercicio. |
==Reducciones cinemáticas de {20} y {01}== | ==Reducciones cinemáticas de {20} y {01}== | ||
| Línea 36: | Línea 36: | ||
<center><math>\vec{v}^P_{21}=(\omega\vec{\jmath}_0)\times(R\vec{k}_0)+(\Omega\vec{k}_0)\times(L\vec{\imath}_0+R\vec{k}_0)=\omega R\vec{\imath}_0+\Omega L\vec{\jmath}_0</math></center> | <center><math>\vec{v}^P_{21}=(\omega\vec{\jmath}_0)\times(R\vec{k}_0)+(\Omega\vec{k}_0)\times(L\vec{\imath}_0+R\vec{k}_0)=\omega R\vec{\imath}_0+\Omega L\vec{\jmath}_0</math></center> | ||
===Aceleración absoluta de P=== | ===Aceleración absoluta de P=== | ||
| - | Usando la ley de composición de | + | Usando la ley de composición de aceleraciones |
<center><math>\vec{a}^P_{21}=\vec{a}^P_{20}+\vec{a}^P_{01}+2\vec{\omega}_{01}\times\vec{v}^P_{20}</math></center> | <center><math>\vec{a}^P_{21}=\vec{a}^P_{20}+\vec{a}^P_{01}+2\vec{\omega}_{01}\times\vec{v}^P_{20}</math></center> | ||
| Línea 61: | Línea 61: | ||
El movimiento absoluto {21}, composición de dos rotaciones puras, no es una rotación pura. | El movimiento absoluto {21}, composición de dos rotaciones puras, no es una rotación pura. | ||
| - | La velocidad angular del movimiento absoluta es la suma de la | + | La velocidad angular del movimiento absoluta es la suma de la del relativo más la del de arrastre |
<center><math>\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}=\omega\vec{\jmath}_0+\Omega\vec{k}_0</math></center> | <center><math>\vec{\omega}_{21}=\vec{\omega}_{20}+\vec{\omega}_{01}=\omega\vec{\jmath}_0+\Omega\vec{k}_0</math></center> | ||
| Línea 83: | Línea 83: | ||
Podemos simplificar esta ecuación escribiéndola como | Podemos simplificar esta ecuación escribiéndola como | ||
| - | <center><math>\overrightarrow{ | + | <center><math>\overrightarrow{OI}=\frac{L\omega^2}{\omega^2+\Omega^2}\vec{\imath}_0 + \omega\left(\frac{R\Omega}{\omega^2+\Omega^2}+\lambda\right)\vec{\jmath}_0+\Omega\left(\frac{R\Omega}{\omega^2+\Omega^2}+\lambda\right)\vec{k}_0</math></center> |
Haciendo | Haciendo | ||
| - | <center><math>\mu = \lambda +\frac{R\Omega}{\omega^2+\Omega^2}\qquad\Rightarrow\qquad \overrightarrow{ | + | <center><math>\mu = \lambda +\frac{R\Omega}{\omega^2+\Omega^2}\qquad\Rightarrow\qquad \overrightarrow{OI}=\frac{L\omega^2}{\omega^2+\Omega^2}\vec{\imath}_0 + \mu(\omega\vec{\jmath}_0+\Omega\vec{k}_0)</math></center> |
que nos dice que el EIRMD pasa por un punto del eje <math>OX_0</math> y corta a este eje perpendicularmente según una dirección contenida en un plano paralelo a <math>OY_0Z_0</math>. | que nos dice que el EIRMD pasa por un punto del eje <math>OX_0</math> y corta a este eje perpendicularmente según una dirección contenida en un plano paralelo a <math>OY_0Z_0</math>. | ||
| Línea 114: | Línea 114: | ||
Vemos que mientras que para la velocidad, la contribución del movimiento de rotación de la hélice y del avión contribuyen en igual medida, para la aceleración la principal contribución, con diferencia, proviene de la rotación de la hélice alrededor de su eje. | Vemos que mientras que para la velocidad, la contribución del movimiento de rotación de la hélice y del avión contribuyen en igual medida, para la aceleración la principal contribución, con diferencia, proviene de la rotación de la hélice alrededor de su eje. | ||
| - | [[Categoría:Problemas de movimiento relativo (G.I.T.I.)]] | + | [[Categoría:Problemas de movimiento relativo (G.I.T.I.)|7]] |
última version al 13:21 24 sep 2013
Contenido |
1 Enunciado
El avión (sólido “0”) de la figura rota alrededor del eje vertical OZ1 de modo que el centro C de su hélice describe una circunferencia de radio L en el sistema de referencia fijo OX1Y1Z1 (sólido “1”). La velocidad angular de esta rotación es constante, su módulo es 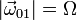 y su sentido el indicado en la figura. Además, la hélice (sólido “2”), cuyo radio es R, rota en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad angular también de módulo constante
y su sentido el indicado en la figura. Además, la hélice (sólido “2”), cuyo radio es R, rota en torno a un eje perpendicular a ella y que pasa por su centro, con velocidad angular también de módulo constante 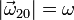 y con el sentido indicado en la figura. Se pide
y con el sentido indicado en la figura. Se pide
- La reducción cinemática de los movimientos {01} y {20}.
- Aplicando las leyes de composición de velocidades y aceleraciones, la velocidad
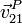 y la aceleración
y la aceleración 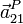 del punto más alto de la hélice (punto P en la figura).
del punto más alto de la hélice (punto P en la figura).
- La reducción cinemática del movimiento {21} en P y la ecuación de su EIRMD ¿Qué tipo de movimiento describe la hélice respecto al sólido “1”?
- Calcule numéricamente
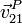 y
y 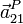 para los valores
para los valores 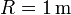 ,
, 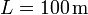 ,
, 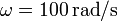 y
y 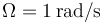 .
.
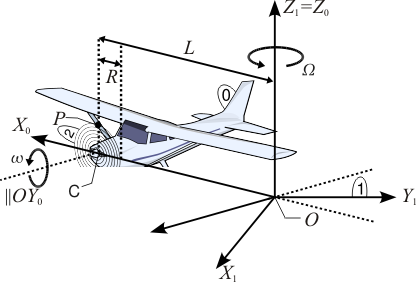
Nota: Se recomienda el uso de la base vectorial asociada al triedro “0” para resolver el ejercicio.
2 Reducciones cinemáticas de {20} y {01}
2.1 Movimiento de arrastre {01}
El movimiento de arrastre es una rotación alrededor del eje permanente OZ0 = OZ1. Si reducimos en un punto de este eje (por ejemplo, en O), tenemos una velocidad de deslizamiento nula y una velocidad angular constante
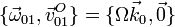
El EIR de este movimiento es el propio eje OZ0.
2.2 Movimiento relativo {20}
El movimiento {20} es también una rotación pura alrededor de un eje fijo, que pasa por el centro de la hélice C. Reduciendo en este punto tenemos
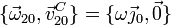
El EIR de este movimiento es uno paralelo a OY0 y que pasa por C.
3 Velocidad y aceleración de P
3.1 Velocidad absoluta de P
La velocidad absoluta de P es la suma de la relativa y la de arrastre
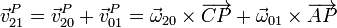
Sustituyendo las velocidades angulares y los vectores de posición relativa queda
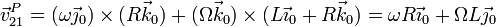
3.2 Aceleración absoluta de P
Usando la ley de composición de aceleraciones
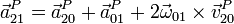
donde los diferentes términos tienen el valor siguiente:
- Aceleración de arrastre {01}
- Es la de una rotación con velocidad angulkar constante en torno a un eje permanente
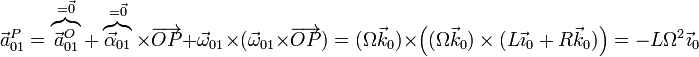
- Aceleración relativa {20}
- Es la de otra rotación alrededor de un eje permanente con velocidad angular constante.
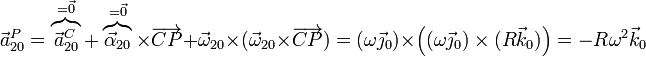
- Término de Coriolis
- Por último tenemos la contribución:
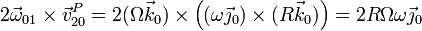
Sumando las tres contribuciones hallamos la aceleración absoluta
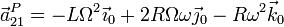
4 Reducción cinemática de {21}
El movimiento absoluto {21}, composición de dos rotaciones puras, no es una rotación pura.
La velocidad angular del movimiento absoluta es la suma de la del relativo más la del de arrastre
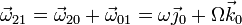
Calculamos la velocidad de deslizamiento proyectando la velocidad de un punto cualquiera sobre la velocidad angular. Puesto que ya conocemos la velocidad de P, podemos emplear este punto
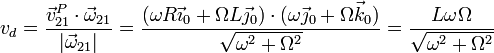
Para hallar la posición del EIRMD empleamos la fórmula general
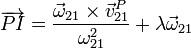
Sustituyendo las diferentes cantidades
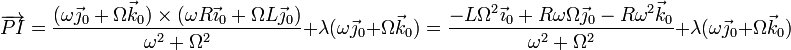
Respecto al punto O, los puntos del eje se encuentran en
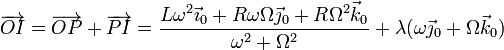
Podemos simplificar esta ecuación escribiéndola como
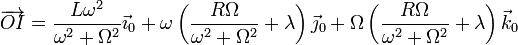
Haciendo
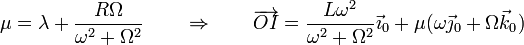
que nos dice que el EIRMD pasa por un punto del eje OX0 y corta a este eje perpendicularmente según una dirección contenida en un plano paralelo a OY0Z0.
Para los puntos de este eje, la reducción cinemática es
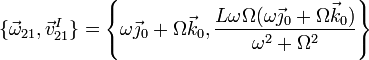
5 Valores numéricos
Sustituyendo los valores del enunciado obtenemos la velocidad
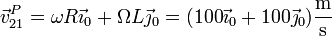
con módulo
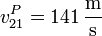
La aceleración en este mismo instante vale
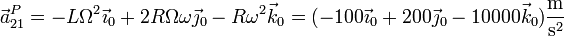
siendo su módulo
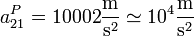
Vemos que mientras que para la velocidad, la contribución del movimiento de rotación de la hélice y del avión contribuyen en igual medida, para la aceleración la principal contribución, con diferencia, proviene de la rotación de la hélice alrededor de su eje.





