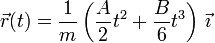Fuerza unidireccional (GIA)
De Laplace
(Página creada con '== Enunciado == Una partícula de masa <math>m</math> está sometida a una fuerza constante <math>\vec{F}=(A + Bt)\,\vec{\imath}</math>. Si parte del reposo y desde el origen de…') |
(→Cálculo de la velocidad) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 35: | Línea 35: | ||
Así pues la velocidad en cada instante es | Así pues la velocidad en cada instante es | ||
<center><math> | <center><math> | ||
| - | \vec{u}(t) = \frac{1}{m}\left(A\,t + \frac{ | + | \vec{u}(t) = \frac{1}{m}\left(A\,t + \frac{1}{2}B\,t^2\right)\,\vec{\imath} |
</math></center> | </math></center> | ||
La condición inicial puede incluirse de otra manera haciendo una integral definida y | La condición inicial puede incluirse de otra manera haciendo una integral definida y | ||
| Línea 43: | Línea 43: | ||
\int\limits_{\vec{u}(0)}^{\vec{u}(t)}\mathrm{d}\vec{u} = \int\limits_0^t\vec{a}\,\mathrm{d} t | \int\limits_{\vec{u}(0)}^{\vec{u}(t)}\mathrm{d}\vec{u} = \int\limits_0^t\vec{a}\,\mathrm{d} t | ||
\Longrightarrow | \Longrightarrow | ||
| - | \vec{u}(t) = \vec{u}(0) + \frac{1}{m}\left(A\,t + \frac{ | + | \vec{u}(t) = \vec{u}(0) + \frac{1}{m}\left(A\,t + \frac{1}{2}B\,t^2\right)\,\vec{\imath} |
</math></center> | </math></center> | ||
Aplicando de nuevo la condición inicial <math>\vec{u}(0)=\vec{0}</math> reobtenemos el resultado | Aplicando de nuevo la condición inicial <math>\vec{u}(0)=\vec{0}</math> reobtenemos el resultado | ||
| Línea 69: | Línea 69: | ||
\vec{r}(t) = \frac{1}{m}\left(\frac{A}{2}t^2 + \frac{B}{6}t^3\right)\,\vec{\imath} | \vec{r}(t) = \frac{1}{m}\left(\frac{A}{2}t^2 + \frac{B}{6}t^3\right)\,\vec{\imath} | ||
</math></center> | </math></center> | ||
| + | |||
| + | |||
| + | [[Categoría:Dinámica del punto material|1]] | ||
| + | [[Categoría:Física I (G.I.A.)]] | ||
| + | [[Categoría:Física I (G.I.T.I.)]] | ||
última version al 14:03 17 dic 2014
Contenido |
1 Enunciado
Una partícula de masa m está sometida a una fuerza constante 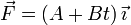 . Si parte del reposo y desde el origen del sistema de referencia, encuentra la posición y la velocidad de la partícula en cualquier instante.
. Si parte del reposo y desde el origen del sistema de referencia, encuentra la posición y la velocidad de la partícula en cualquier instante.
2 Solución
Para determinar el movimiento de la partícula usamos la Segunda ley de Newton, que dice
que una partícula de masa m sometida a una fuerza  adquiere una aceleración
adquiere una aceleración
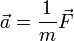
2.1 Cálculo de la velocidad
El enunciado nos dice que la fuerza es 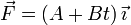 , con A y B constantes. Así
pues la aceleración de la partícula es
, con A y B constantes. Así
pues la aceleración de la partícula es

La aceleración es la derivada respecto al tiempo de la velocidad. Integrando tenemos

El vector 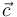 es una constante que viene determinada por las condiciones
iniciales. Introduciendo la expresión de la aceleración obtenemos
es una constante que viene determinada por las condiciones
iniciales. Introduciendo la expresión de la aceleración obtenemos
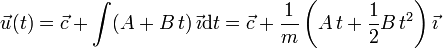
El enunciado dice que la partícula parte del reposo. Por tanto, en t = 0 la velocidad es nula. Obtenemos

Así pues la velocidad en cada instante es
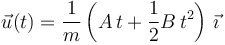
La condición inicial puede incluirse de otra manera haciendo una integral definida y teniéndola en cuenta en los límites de integración. La ecuación \reff{eq:3} se reescribiría

Aplicando de nuevo la condición inicial 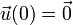 reobtenemos el resultado
anterior.
reobtenemos el resultado
anterior.
2.2 Cálculo de la posición
La velocidad es la derivada del vector de posición en el tiempo. Procedemos igual que en el cálculo anterior y tenemos
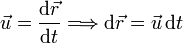
Usamos la integral definida con las condiciones iniciales incluidas en los límites de integración
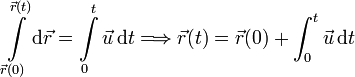
El enunciado dice que la partícula parte desde el origen des sistema de referencia, por lo
que 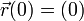 . Utilizando la expresión de la velocidad obtenemos
. Utilizando la expresión de la velocidad obtenemos