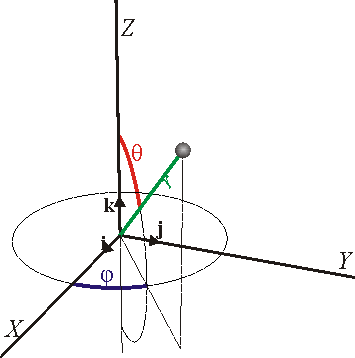
Coordenadas esféricas. Definición
De Laplace
(→Artículo anterior) |
(→Definición) |
||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 10: | Línea 10: | ||
<math>r\in [0,\infty)\qquad \theta\in [0,\pi]\qquad{\varphi} \in (-\pi,\pi]</math> | <math>r\in [0,\infty)\qquad \theta\in [0,\pi]\qquad{\varphi} \in (-\pi,\pi]</math> | ||
| - | El ángulo <math>\varphi</math> también puede variar en el intervalo | + | El ángulo <math>\varphi</math> también puede variar en el intervalo <math>[0,2\pi)</math>. |
===<math>r\,</math> es siempre positiva=== | ===<math>r\,</math> es siempre positiva=== | ||
| Línea 41: | Línea 41: | ||
La coordenada radial sería la distancia a la cual se encuentran las estrellas respecto de la Tierra. | La coordenada radial sería la distancia a la cual se encuentran las estrellas respecto de la Tierra. | ||
| - | == | + | ==Enlaces== |
| - | [[Relación entre los distintos sistemas de coordenadas]] | + | * '''Siguiente:''' [[Relación entre los distintos sistemas de coordenadas]] |
| - | + | * '''Anterior:''' [[Coordenadas cilíndricas. Definición]] | |
| - | [[Coordenadas cilíndricas. Definición]] | + | * [[Coordenadas esféricas. Líneas y superficies coordenadas]] |
| + | * [[Coordenadas esféricas. Base vectorial]] | ||
| - | + | [[Categoría:Definición de sistemas|40]] | |
| - | [[ | + | [[Categoría:Coordenadas esféricas|10]] |
| - | + | ||
| - | [[ | + | |
última version al 19:53 12 feb 2010
Contenido |
1 Definición
Las coordenadas esféricas constituyen otra generalización de las coordenadas polares del plano, a base de girarlas alrededor de un eje. Su definición es la siguiente:- La coordenada radial
 : distancia al origen
: distancia al origen
- La coordenada polar
 : ángulo que el vector de posición forma con el eje
: ángulo que el vector de posición forma con el eje 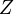 .
.
- La coordenada acimutal
 : ángulo que la proyección sobre el plano
: ángulo que la proyección sobre el plano 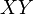 forma con el eje
forma con el eje 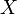 .
.
Los rangos de variación de estas coordenadas son:
![r\in [0,\infty)\qquad \theta\in [0,\pi]\qquad{\varphi} \in (-\pi,\pi]](/wiki/images/math/f/c/d/fcd60e4cd9442b416c815f755cb66913.png)
El ángulo  también puede variar en el intervalo [0,2π).
también puede variar en el intervalo [0,2π).
1.1  es siempre positiva
es siempre positiva
La coordenada radial es una distancia siempre positiva. Si, partiendo de un punto  , vamos reduciendo el valor de
, vamos reduciendo el valor de  , al atravesar el origen de coordenadas
, al atravesar el origen de coordenadas  vuelve a aumentar. Lo que cambian son los valores de
vuelve a aumentar. Lo que cambian son los valores de  , que pasa a valer
, que pasa a valer 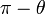 (¿Por qué?) y
(¿Por qué?) y  , que pasa a ser
, que pasa a ser 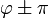 (¿Por qué?).
(¿Por qué?).
1.2  vale
vale 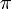 como mucho, no
como mucho, no 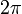
Es un error muy común el suponer que  llega hasta
llega hasta 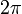 , como
, como 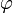 . Hay que recordar que ambas coordenadas tienen significados geométricos muy diferentes.
. Hay que recordar que ambas coordenadas tienen significados geométricos muy diferentes. 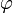 equivale a la longitud geográfica, mientras que
equivale a la longitud geográfica, mientras que  es el complementario de la latitud.
es el complementario de la latitud.
El valor 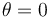 corresponde al Polo Norte. Si ahora aumentamos
corresponde al Polo Norte. Si ahora aumentamos  , lo que hacemos es viajar hacia al sur. El Polo Sur es
, lo que hacemos es viajar hacia al sur. El Polo Sur es 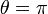 . Y es lo máximo a lo que podemos llegar. No se puede viajar al sur del Polo Sur. Si siguiéramos recorriendo la superficie terrestre lo que estaríamos haciendo es ya volver hacia el norte, lo que supone reducir
. Y es lo máximo a lo que podemos llegar. No se puede viajar al sur del Polo Sur. Si siguiéramos recorriendo la superficie terrestre lo que estaríamos haciendo es ya volver hacia el norte, lo que supone reducir  . Eso sí, al pasar por el Polo Sur, la longitud
. Eso sí, al pasar por el Polo Sur, la longitud 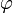 cambia a
cambia a 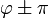 .
.
1.3 Geografía...
El uso más evidente de las coordenadas esféricas lo constituye la geografía. Para identificar un punto de la superficie terrestre indicamos su latitud y su longitud.La latitud es la altura respecto al ecuador. Este ángulo es el complementario de la coordenada polar  (por lo cual a ésta se la llama también colatitud). La latitud, en lugar de variar de
(por lo cual a ésta se la llama también colatitud). La latitud, en lugar de variar de  (en el Polo Norte) a
(en el Polo Norte) a 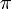 (en el Polo Sur) lo hace desde
(en el Polo Sur) lo hace desde 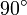 a
a 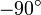 .
.
La longitud es la distancia angular respecto a un meridiano fijo (el de Greenwich). Equivale a la coordenada acimutal 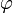 .
.
La coordenada radial corresponde a la distancia al centro de la Tierra. La altitud  de un punto de la superficie equivale al valor de
de un punto de la superficie equivale al valor de 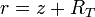 con
con 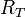 el radio de la Tierra (suponiendo ésta una esfera, lo
que es solo una aproximación).
el radio de la Tierra (suponiendo ésta una esfera, lo
que es solo una aproximación).
1.4 ...y astronomía
Para situar las estrellas en el firmamento también es preciso emplear coordenadas esféricas. Existen varias posibilidades, siendo la más usada la formada por la ascensión recta y la declinación.La declinación es el equivalente de la latitud, medida en este caso respecto al ecuador celeste y la ascensión recta corresponde a la longitud, medida desde un punto de referencia conocido como punto vernal (o punto Aries).
La coordenada radial sería la distancia a la cual se encuentran las estrellas respecto de la Tierra.