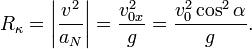Entrar Página Discusión Historial Go to the site toolbox

Tiro oblicuo (G.I.A.)

De Laplace

(Diferencias entre revisiones)
(→Caso 2)
(→Movimiento del proyectil)
 
(2 ediciones intermedias no se muestran.)
Línea 3: Línea 3:
== Solución ==
== Solución ==
-
El campo gravitatorio ejerce una fuerza <math>\vec{F}=m\,\vec{g}</math> sobre una partícula de masa <math>m</math>.
+
 
-
Según la Segunda Ley de Newton la aceleración de la partícula es
+
===Movimiento del proyectil===
 +
 
 +
El proyectil está sometido a la acción de la gravedad, es decir, a una aceleración uniforme. Elegimos
 +
el sistema de referencia como se indica en el dibujo, con el eje <math>OX</math> sobre la horizontal y el eje <math>OY</math>
 +
vertical al suelo. En este sistema de referencia, la gravedad es
<center><math>
<center><math>
-
   \vec{a} = \dfrac{1}{m}\vec{F} = \dfrac{1}{m}m\,\vec{g} = \vec{g}
+
   \vec{g} = -g\,\vec{\jmath}
</math></center>
</math></center>
-
El enunciado nos da un sistema de ejes en el que la aceleración de la gravedad está
+
La ecuación que determina la velocidad en función del tiempo es
-
dirigida en el sentido negativo del eje <math>OZ</math>, esto es
+
[[Imagen:F1_GIA_p03_03.png|right]]
<center><math>
<center><math>
-
   \vec{g} = -g\,\vec{k}
+
   \mathrm{d}\vec{v} = \vec{a}_0\mathrm{d} t\to
 +
\left\{
 +
  \begin{array}{l}
 +
    \mathrm{d} v_x = 0\\
 +
    \mathrm{d} v_y = -g\mathrm{d} t\\
 +
    \mathrm{d} v_z = 0
 +
  \end{array}
 +
\right.
</math></center>
</math></center>
-
La velocidad de la partícula se calcula como la integral del vector aceleración en el
+
Integrando una vez resulta
-
tiempo. Si la velocidad inicial es <math>\vec{v}(0)</math> tenemos
+
<center><math>
<center><math>
-
  \int\limits_{\vec{v}(0)}^{\vec{v}(t)}\mathrm{d}\vec{v} = \int\limits_0^t\vec{a}\,\mathrm{d} t
+
\vec{v}(t) =
-
  \Longrightarrow
+
\left\{
-
     \vec{v}(t) = \vec{v}(0) - \int\limits_0^t g\,\vec{k}\,\mathrm{d} t
+
  \begin{array}{l}
 +
    v_x = v_{x0}\\
 +
     v_y = v_{y0}-g t\\
 +
    v_z = v_{z0}
 +
  \end{array}
 +
\right.
</math></center>
</math></center>
-
Teniendo en cuenta que <math>g</math> y <math>\vec{k}</math> son constantes podemos hacer la integral para obtener
+
La velocidad inicial es
<center><math>
<center><math>
-
   \vec{v}(t) = \vec{v}(0) - g\,t\,\vec{k}
+
   \vec{v}_0 = \left( v_0\cos\alpha,v_0\,\mathrm{sen}\,\alpha,0\right)
</math></center>
</math></center>
-
La posición se determina de modo similar integrando la velocidad
+
Con lo que la evolución de la velocidad en el tiempo es
<center><math>
<center><math>
-
   \int\limits_{\vec{r}(0)}^{\vec{r}(t)}\mathrm{d}\vec{r} = \int\limits_0^t \vec{v} \,\mathrm{d} t
+
   \vec{v}(t) = (v_0\cos\alpha,v_0\,\mathrm{sen}\,\alpha-g t,0)
-
  \Longrightarrow
+
-
  \vec{r}(t) = \vec{r}(0) + \int\limits_0^t\left(\vec{v}(0) - g\,t\,\vec{k} \right)\,\mathrm{d} t
+
</math></center>
</math></center>
-
Como <math>\vec{v}(0)</math>, <math>g</math> y <math>\vec{k}</math> son constantes obtenemos
+
Obtenemos la posición en cada instante del proyectil integrando la
 +
ecuación
<center><math>
<center><math>
-
   \vec{r}(t) = \vec{r}(0) + \vec{v}(0)\,t - \dfrac{1}{2}g\,t^2\,\vec{k}
+
   \mathrm{d}\vec{r} = \vec{v}(t)\mathrm{d} t\to
-
</math></center>
+
\left\{
-
Las expresiones para <math>\vec{r}(t) </math> y <math>\vec{v}(t) </math>  describen el movimiento genérico de una partícula en el seno del
+
-
campo gravitatorio. El movimiento concreto depende del valor de estas condiciones
+
-
iniciales. Vamos a ver los tres casos descritos en el enunciado.
+
-
 
+
-
===Caso 1===
+
-
 
+
-
[[Imagen:F1_GIA_p04_03_a.png|right]]
+
-
[[Imagen:F1_GIA_p04_03_b.png|right]]
+
-
Sustituyendo las condiciones iniciales tenemos
+
-
<center><math>
+
-
  \left.
+
   \begin{array}{l}
   \begin{array}{l}
-
     \vec{v}(t) = (v_0 - g\,t) \, \vec{k} \\ \\
+
     \mathrm{d} x = v_x(t)\mathrm{d} t = v_{x0}\,\mathrm{d} t\\
-
     \vec{r}(t) = \left(v_0t-\dfrac{1}{2}g\,t^2\right)\,\vec{k}
+
     \mathrm{d} y = v_y(t)\mathrm{d} t= (v_{y0} - g t)\,\mathrm{d} t\\
 +
    \mathrm{d} z = v_z(t)\mathrm{d} t= 0
   \end{array}
   \end{array}
-
  \right.
+
\right.
</math></center>
</math></center>
-
Tanto la velocidad como el vector de posición son paralelos al eje <math>OZ</math> en todo instante
+
Integrando obtenemos
-
de tiempo. En <math>t=0</math> la velocidad es positiva (suponiendo <math>v_0>0</math>)  por lo que la partícula
+
<center><math>
-
sube verticalmente. AL avanzar el tiempo el término <math>gt\,</math> crece, hasta que iguala a <math>v_0</math>
+
  \vec{r}(t) =
-
y lo sobrepasa. En ese instante la velocidad es negativa y la partícula se desplaza hacia
+
  \left\{
-
abajo. La trayectoria es una línea recta. Este caso corresponde al '''tiro vertical'''.
+
    \begin{array}{l}
 +
      x = v_{x0}\,t\\
 +
      y = v_{y0}\,t-\dfrac{1}{2}gt^2\\
 +
      z = 0
 +
    \end{array}
 +
\right.
 +
</math></center>
 +
Hemos supuesto que el movimiento parte del origen del sistema de
 +
referencia.
-
El instante para el que la altura es máxima corresponde al momento en que la velocidad se
+
El punto de máxima altura se obtiene cuando la velocidad vertical se
-
hace cero
+
anula. Igualando a cero la velocidad <math>v_y(t)</math>
 +
obtenemos
<center><math>
<center><math>
-
   v(t_{max}) = 0 \Longrightarrow t_{max} = v_0/g
+
   T_m = \dfrac{v_{y0}}{g}=\dfrac{v_0\,\mathrm{sen}\,\alpha}{g}
</math></center>
</math></center>
-
La altura máxima que alcanza la partícula se obtiene sustituyendo <math>t_{max}</math> en la
+
En este instante la velocidad y la aceleración son perpendiculares, es
-
expresión que da el vector de posición
+
decir, la aceleración es
<center><math>
<center><math>
-
   \vec{r}(t_{max}) = \dfrac{v_0^2}{2g}\,\vec{k}
+
   \vec{a} = a_N(T_m)\vec{N} = -g\vec{\jmath} = \dfrac{v^2}{R_{\kappa}}\vec{\jmath}.
</math></center>
</math></center>
-
La figura muestra la orientación de la velocidad y el vector de posición antes y después
+
Por tanto el radio de curvatura es
-
de que la partícula alcance su máxima altura. A la derecha están representados la
+
<center><math>
-
evolución en el tiempo de  la velocidad y la altura para el caso <math>v_0=1\,\mathrm{m/s}</math>. El
+
  R_{\kappa} = \left|\dfrac{v^2}{a_N}\right| = \dfrac{v_{0x}^2}{g} =
-
máximo de la altura corresponde al cero de la velocidad, como debe ser pues la velocidad
+
  \dfrac{v_0^2\cos^2\alpha}{g}.
-
es la derivada de la altura. Mientras que la velocidad es positiva la altura crece, y
+
</math></center>
-
cuando se hace negativa decrece.
+
 
 +
[[Categoría:Cinemática del punto material|1]]
 +
[[Categoría:Física I (G.I.A.)]]
 +
[[Categoría:Física I (G.I.T.I.)]]

última version al 09:42 2 nov 2010

1 Enunciado

Determina el movimiento de un proyectil disparado con una velocidad inicial v0 y un ángulo α con la horizontal. El proyectil está sometido a la acción de la gravedad. Calcula el radio de curvatura en el punto más alto de su trayectoria.

2 Solución

2.1 Movimiento del proyectil

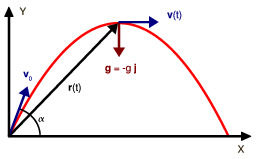
El proyectil está sometido a la acción de la gravedad, es decir, a una aceleración uniforme. Elegimos el sistema de referencia como se indica en el dibujo, con el eje OX sobre la horizontal y el eje OY vertical al suelo. En este sistema de referencia, la gravedad es

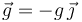
\vec{g} = -g\,\vec{\jmath}

La ecuación que determina la velocidad en función del tiempo es

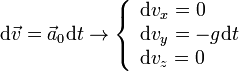
\mathrm{d}\vec{v} = \vec{a}_0\mathrm{d} t\to \left\{ \begin{array}{l} \mathrm{d} v_x = 0\\ \mathrm{d} v_y = -g\mathrm{d} t\\ \mathrm{d} v_z = 0 \end{array} \right.

Integrando una vez resulta

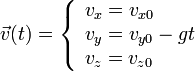
\vec{v}(t) = \left\{ \begin{array}{l} v_x = v_{x0}\\ v_y = v_{y0}-g t\\ v_z = v_{z0} \end{array} \right.

La velocidad inicial es

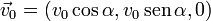
\vec{v}_0 = \left( v_0\cos\alpha,v_0\,\mathrm{sen}\,\alpha,0\right)

Con lo que la evolución de la velocidad en el tiempo es

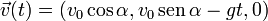
\vec{v}(t) = (v_0\cos\alpha,v_0\,\mathrm{sen}\,\alpha-g t,0)

Obtenemos la posición en cada instante del proyectil integrando la ecuación

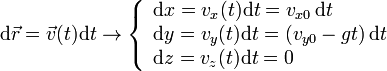
\mathrm{d}\vec{r} = \vec{v}(t)\mathrm{d} t\to \left\{ \begin{array}{l} \mathrm{d} x = v_x(t)\mathrm{d} t = v_{x0}\,\mathrm{d} t\\ \mathrm{d} y = v_y(t)\mathrm{d} t= (v_{y0} - g t)\,\mathrm{d} t\\ \mathrm{d} z = v_z(t)\mathrm{d} t= 0 \end{array} \right.

Integrando obtenemos

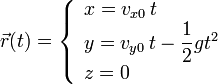
\vec{r}(t) = \left\{ \begin{array}{l} x = v_{x0}\,t\\ y = v_{y0}\,t-\dfrac{1}{2}gt^2\\ z = 0 \end{array} \right.

Hemos supuesto que el movimiento parte del origen del sistema de referencia.

El punto de máxima altura se obtiene cuando la velocidad vertical se anula. Igualando a cero la velocidad vy(t) obtenemos

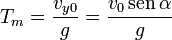
T_m = \dfrac{v_{y0}}{g}=\dfrac{v_0\,\mathrm{sen}\,\alpha}{g}

En este instante la velocidad y la aceleración son perpendiculares, es decir, la aceleración es

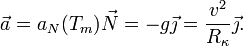
\vec{a} = a_N(T_m)\vec{N} = -g\vec{\jmath} = \dfrac{v^2}{R_{\kappa}}\vec{\jmath}.

Por tanto el radio de curvatura es

R_{\kappa} = \left|\dfrac{v^2}{a_N}\right| = \dfrac{v_{0x}^2}{g} = \dfrac{v_0^2\cos^2\alpha}{g}.
Obtenido de "http://tesla.us.es/wiki/index.php/Tiro_oblicuo_(G.I.A.)"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Esta página fue modificada por última vez el 09:42, 2 nov 2010. - Esta página ha sido visitada 5.273 veces. - Aviso legal - Acerca de Laplace