Ciclo de Stirling
De Laplace
(→Descripción del ciclo) |
(→Rendimiento) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 20: | Línea 20: | ||
===Rendimiento=== | ===Rendimiento=== | ||
| + | En este proceso se absorbe calor en al calentamiento isócoro y la expansión isoterma, y se cede en los otros dos procesos. El valor neto del calor absorbido es | ||
| + | |||
| + | <center><math>|Q_c|=nc_v(T2-T1)+nRT_2\ln\left(\frac{V_A}{V_B}\right)</math></center> | ||
| + | |||
| + | y del cedido | ||
| + | |||
| + | <center><math>|Q_f|=nc_v(T2-T1)+nRT_1\ln\left(\frac{V_A}{V_B}\right)</math></center> | ||
| + | |||
| + | de forma que el rendimiento es | ||
| + | |||
| + | <center><math>\eta = 1 -\frac{|Q_f|}{|Q_c|}= 1- \frac{c_v(T_2-T_1) + RT_1\ln(r)}{c_v(T_2-T_1)+RT_2\ln(r)}</math></center> | ||
| + | |||
| + | siendo <math>r</math> la relación de compresión. | ||
| + | |||
| + | Podemos comprobar que este rendimiento es siempre menor que el de una máquina reversible que opere entre estas dos temperaturas | ||
| + | |||
| + | <center><math>\eta_\mathrm{max}=1-\frac{T_1}{T_2}</math></center> | ||
| + | |||
| + | siendo la diferencia | ||
| + | |||
| + | <center><math>\eta_\mathrm{max}-\eta = \frac{c_v(T_2-T_1)^2}{T_2(c_v(T_2-T_1)+RT_2\ln(r))}>0</math></center> | ||
==Intercambiador de calor== | ==Intercambiador de calor== | ||
última version al 23:00 14 may 2010
Contenido |
1 Introducción
El ciclo de Stirling es un ejemplo, como el ciclo de Carnot de ciclo completamente reversible y que por tanto alcanza el máximo rendimiento que permite el Segundo Principio de la Termodinámica.
Se trata de un ciclo altamente ideal cuya realización práctica, incluso en forma aproximada entraña serias dificultades. No obstante, en los últimos años ha adquirido relevancia con el desarrollo de motores de Stirling, que funcionan de manera aproximada según este ciclo.
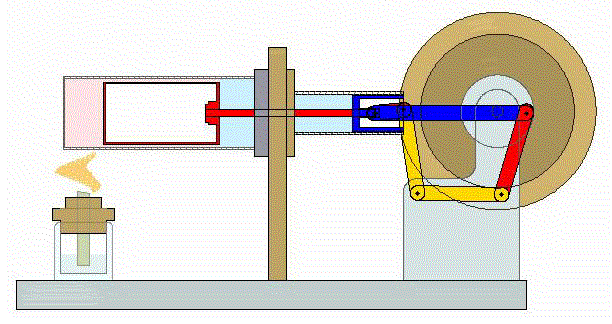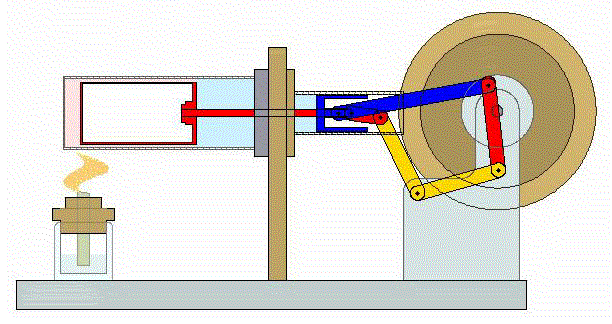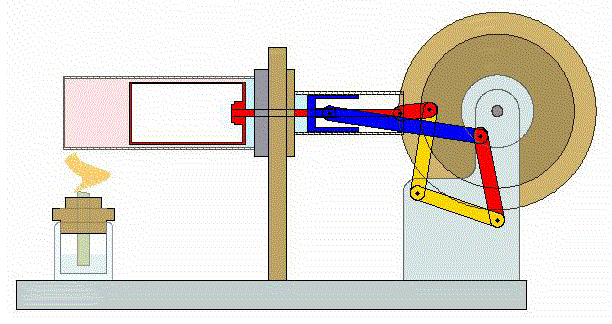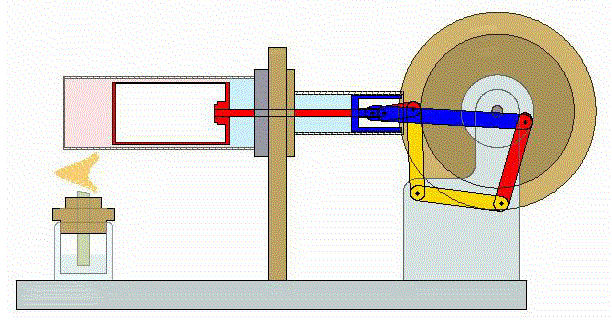
2 Descripción del ciclo
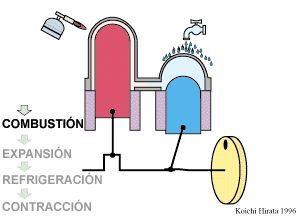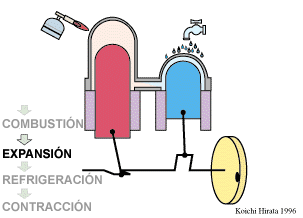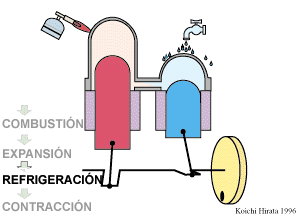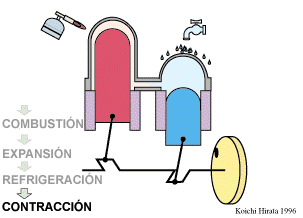
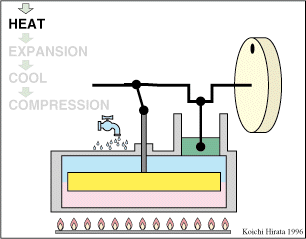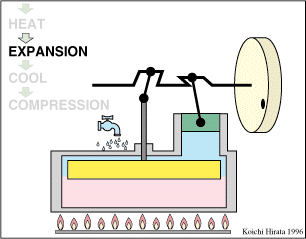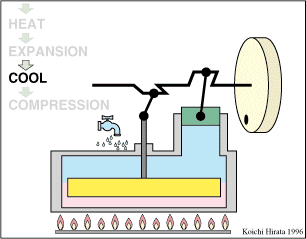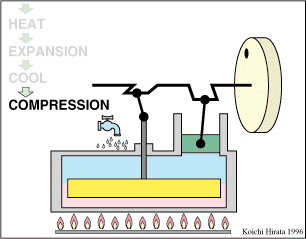
Un ciclo de Stirling ideal se compone de cuatro procesos reversibles:
- Compresión isoterma A→B
- El gas se comprime desde un volumen inicial VA hasta uno final VB, inferior, manteniendo su temperatura constante en un valor T1 (a base de enfriar el gas de forma continuada).
- Calentamiento a volumen constante B→C
- El gas se calienta desde la temperatura T1 a la temperatura T2 mantenientdo fijo su volumen.
- Expansión isoterma C→D
- El gas se expande mientras se le suministra calor de forma que su temperatura permanece en su valor T2.
- Enfriamiento isócoro D→A
- Se reduce la temperatura del gas de nuevo a su valor T1 en un proceso a volumen constante.
2.1 Rendimiento
En este proceso se absorbe calor en al calentamiento isócoro y la expansión isoterma, y se cede en los otros dos procesos. El valor neto del calor absorbido es
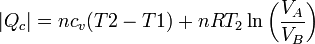
y del cedido
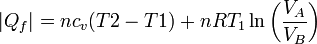
de forma que el rendimiento es

siendo r la relación de compresión.
Podemos comprobar que este rendimiento es siempre menor que el de una máquina reversible que opere entre estas dos temperaturas
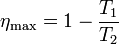
siendo la diferencia
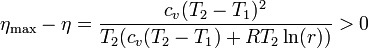
3 Intercambiador de calor
Lo que hace especial al ciclo de Stirling (y al de Ericsson, que es análogo pero con procesos isóbaros en lugar de isócoros) es la presencia de un intercambiador de calor. En el enfriamiento del gas, se pasa de la temperatura T2 a T1 liberando calor. En el calentamiento, se pasa de T1 a T2, absorbiendo calor. Puesto que se pasa por las mismas temperaturas es (teóricamente) posible aprovechar el calor liberado al enfriarse sin violar el segundo principio de la termodinámica: el calor que se va liberando gradualmente en un punto del enfriamiento se cede al punto a la misma temperatura en el calentamiento. Puesto que ambos puntos se encuentran a la misma temperatura el proceso es reversible.





