Mezcla de agua y vapor
De Laplace
(→Solución) |
(→Solución) |
||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
== Enunciado == | == Enunciado == | ||
| - | En un calorímetro que contiene 200 g de hielo a -8.00 | + | En un calorímetro que contiene 200 g de hielo a -8.00 °C se introducen 50.0 g de vapor de agua a 100 °C. El equivalente en agua del calorímetro es 20.0 g. Determina el estado final de la mezcla. |
| - | Datos: calor específico del hielo: 0.500 cal/g | + | Datos: calor específico del hielo: 0.500 cal/g °C; entalpía de fusión del hielo: 80.0cal/g; entalpía de vaporización del agua: 537 cal/g |
== Solución == | == Solución == | ||
| - | Supongamos que el estado final de la mezcla es agua líquida a una cierta | + | Supongamos que el estado final de la mezcla es agua líquida a una cierta temperatura. El vapor tiene que condensarse en agua líquida y después enfriarse hasta la temperatura final. Por su parte, el hielo tiene que calentarse para llegar a 0°C, luego derretirse y después calentarse hasta la temperatura final de la mezcla. Además hay que tener en cuenta el calor intercambiado por el calorímetro. El proceso que sigue cada uno de los sistemas es |
| - | temperatura. El vapor tiene que condensarse en agua líquida y después | + | |
| - | enfriarse hasta la temperatura final. Por su parte, el hielo | + | |
| - | tiene que calentarse para llegar a 0 | + | |
| - | después calentarse hasta la temperatura final de la mezcla. Además hay | + | |
| - | que tener en cuenta el calor intercambiado por el calorímetro. El proceso | + | |
| - | que sigue cada uno de los sistemas es | + | |
<center> | <center> | ||
<math> | <math> | ||
| Línea 78: | Línea 72: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | La capacidad calorífica del calorímetro es el productor de su equivalente en agua por | + | La capacidad calorífica del calorímetro es el productor de su equivalente en agua por el calor específico del agua líquida |
| - | el calor específico del agua líquida | + | |
<center> | <center> | ||
<math> | <math> | ||
| Línea 97: | Línea 90: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | El calor de fusión entra con signo positivo pues el hielo absorbe calor para derretirse, | + | El calor de fusión entra con signo positivo pues el hielo absorbe calor para derretirse, mientras que el calor de vaporización entra con signo negativo pues el vapor cede calor al condensarse. Obsérvese que el calorímetro no se ve afectado por cambios de fase. El dato del equivalente en agua del vaso nos sirve para calcular su capacidad calorífica, pero no significa que cambie de fase como el agua. |
| - | mientras que el calor de vaporización entra con signo negativo pues el vapor cede | + | |
| - | calor al condensarse. | + | |
| - | Obsérvese que el calorímetro no se ve afectado por cambios de fase. El dato del equivalente | + | |
| - | en agua del vaso nos sirve para calcular su capacidad calorífica, pero no significa que | + | |
| - | cambie de fase como el agua. | + | |
| - | + | ||
Como el sistema está aislado debe cumplirse | Como el sistema está aislado debe cumplirse | ||
| Línea 118: | Línea 105: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | La temperatura final es coherente con la suposición que hemos hecho de que el estado | + | La temperatura final es coherente con la suposición que hemos hecho de que el estado final de la mezcla es agua líquida a una cierta temperatura. Si hubiese salido una temperatura negativa querría decir que en el estado final habría hielo no derretido, mientras que si hubiese salido mayor que 100 °C querría decir que parte del vapor no se condensa. En esos casos habría que modificar los procesos que siguen cada uno de los sistemas. |
| - | final de la mezcla es agua líquida a una cierta temperatura. Si hubiese salido una | + | |
| - | temperatura negativa querría decir que en el estado final habría hielo no derretido, | + | [[Categoría:Problemas del primer principio de la termodinámica]] |
| - | mientras que si hubiese salido mayor que 100 | + | |
| - | vapor no se condensa. En esos casos habría que modificar los procesos que siguen | + | |
| - | cada uno de los sistemas. | + | |
última version al 22:48 11 may 2010
1 Enunciado
En un calorímetro que contiene 200 g de hielo a -8.00 °C se introducen 50.0 g de vapor de agua a 100 °C. El equivalente en agua del calorímetro es 20.0 g. Determina el estado final de la mezcla.
Datos: calor específico del hielo: 0.500 cal/g °C; entalpía de fusión del hielo: 80.0cal/g; entalpía de vaporización del agua: 537 cal/g
2 Solución
Supongamos que el estado final de la mezcla es agua líquida a una cierta temperatura. El vapor tiene que condensarse en agua líquida y después enfriarse hasta la temperatura final. Por su parte, el hielo tiene que calentarse para llegar a 0°C, luego derretirse y después calentarse hasta la temperatura final de la mezcla. Además hay que tener en cuenta el calor intercambiado por el calorímetro. El proceso que sigue cada uno de los sistemas es
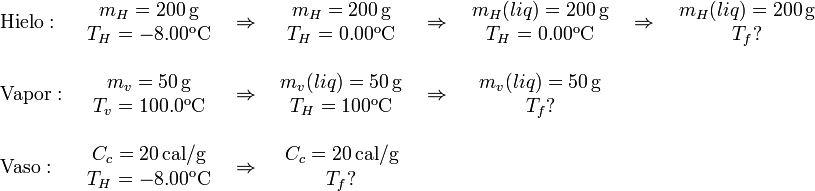
La capacidad calorífica del calorímetro es el productor de su equivalente en agua por el calor específico del agua líquida
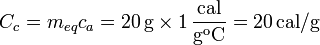
Ahora podemos calcular el calor transferido por cada uno de los sistemas
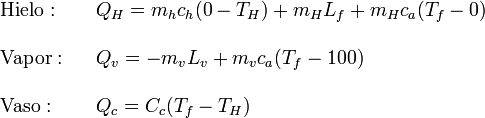
El calor de fusión entra con signo positivo pues el hielo absorbe calor para derretirse, mientras que el calor de vaporización entra con signo negativo pues el vapor cede calor al condensarse. Obsérvese que el calorímetro no se ve afectado por cambios de fase. El dato del equivalente en agua del vaso nos sirve para calcular su capacidad calorífica, pero no significa que cambie de fase como el agua.
Como el sistema está aislado debe cumplirse
QH + Qv + Qc = 0
Esto nos da una ecuación para una incógnita, la temperatura final de la mezcla. Obtenemos
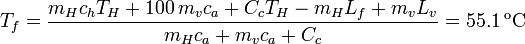
La temperatura final es coherente con la suposición que hemos hecho de que el estado final de la mezcla es agua líquida a una cierta temperatura. Si hubiese salido una temperatura negativa querría decir que en el estado final habría hielo no derretido, mientras que si hubiese salido mayor que 100 °C querría decir que parte del vapor no se condensa. En esos casos habría que modificar los procesos que siguen cada uno de los sistemas.





