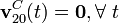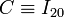Disco arrastrando una varilla

De Laplace

(Diferencias entre revisiones)

Revisión de 15:06 3 feb 2010

1 Enunciado

(Primer Parcial, Enero 2010, P1)

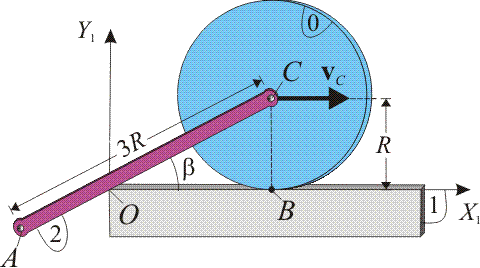
En el sistema de la figura los tres sólidos realizan un movimiento plano cuando el disco de radio

R

(sólido “0”) rueda sin deslizar sobre el sólido “1”. El centro del disco,

C

, se desplaza con una velocidad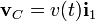 $\mathbf{v}_C=v(t)\mathbf{i}_1$ . La barra de longitud

3 R

(sólido “2”) tiene su extremo

C

articulado en el centro del disco, mientras que se apoya en el borde

O

del sólido “1”.

Determine gráficamente la posición de los C.I.R. de los movimientos {21}, {20} y {01}.
En el instante en que la distancia entre los puntos $O$ y $B$ es igual a $R$ , la velocidad del punto $C$ es 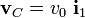$\mathbf{v}_C=v_0\ \mathbf{i}_1$ . Calcule las reducciones cinemáticas de los tres movimientos en el punto $C$ .
Exprese el vector de posición del punto $A$ en el sistema “1”, 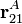$\mathbf{r}_{21}^A$ , en función de un ángulo $β$ arbitrario.
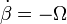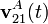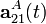Si $\dot{\beta}=-\Omega$ , con $Ω$ constante y positiva, calcule $\mathbf{v}_{21}^A(t)$ y $\mathbf{a}_{21}^A(t)$ para todo instante de tiempo, en función de $β$ , $Ω$ y $R$ .

2 Solución

Como paso previo a la solución de los distintos apartados procederemos a adoptar los sistemas de referencia equivalentes a los distintos sólidos rígidos del sistema bajo estudio. En la figura del enunciado se indican los ejes 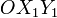$\displaystyle OX_1Y_1$ asocidados al sólido “1”, respecto del cuál, el disco “0” y la varilla “2” realizan sendos movimientos planos {01} y {21}, que tienen como plano director al definido por aquellos ejes; es decir, la dirección normal a dicho plano esta definida por el eje $O Z 1$ . Tal como se muestra en la figura, resulta conveniente adoptar sistemas de referencia ligados a los sólidos móviles “0” y “2” cuyas direcciones $C Z 0$ y $A Z 2$ sean también perpendiculares a dicho plano director. Tomando como eje $A X 2$ la dirección 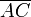$\overline{AC}$ definida por la varilla “2”, que forma un ángulo $β$ con el eje $O X 1$ , y como eje $C X 0$ una dirección arbitraria contenida en el disco “0”, se tendrá la siguiente relación entre los vectores de los triedros cartesianos asociados a cada uno de los sólidos:

$\begin{array}{l}\displaystyle \mathbf{i}_2=\cos\beta\ \mathbf{i}_1+\mathrm{sen} \beta\ \mathbf{j}_1 \\ \displaystyle \mathbf{j}_2=-\mathrm{sen} \beta\ \mathbf{i}_1+\cos\beta\ \mathbf{j}_1\\ \displaystyle \mathbf{k}_2=\mathbf{k}_1 \end{array}\qquad \qquad \qquad \qquad\begin{array}{l}\displaystyle \mathbf{i}_0=\cos\varphi\ \mathbf{i}_1-\mathrm{sen} \varphi\ \mathbf{j}_1 \\ \displaystyle \mathbf{j}_0=\mathrm{sen} \varphi\ \mathbf{i}_1+\cos\varphi\ \mathbf{j}_1\\ \displaystyle \mathbf{k}_0=\mathbf{k}_1 \end{array}$

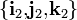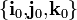Los movimientos relativos de los sólidos “2” y “0” respecto del sólido fijo “1” se corresponderán con sendas leyes horarias $β(t)$ y $\varphi(t)$ que describen cómo cambian en el tiempo dichos ángulos y, por tanto, cómo se mueven los triedros $\{\mathbf{i}_2\mathrm{,}\mathbf{j}_2\mathrm{,}\mathbf{k}_2\}$ y $\{\mathbf{i}_0\mathrm{,}\mathbf{j}_0\mathrm{,}\mathbf{k}_0\}$ , respecto del 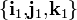$\{\mathbf{i}_1\mathrm{,}\mathbf{j}_1\mathrm{,}\mathbf{k}_1\}$ . Además, aplicando las fórmulas de Poisson podemos establecer la relación entre las derivadas de dichas leyes horarias y los vectores rotación instaneas de los movimientos {01} y {21}:

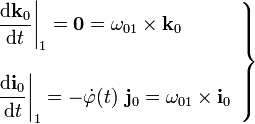
$\left.\begin{array}{l}\displaystyle \frac{\mathrm{d}\mathbf{k}_0}{\mathrm{d}t}\bigg|_1=\mathbf{0}=\mathbf{\omega}_{01}\times\mathbf{k}_0 \\ {} \\ \displaystyle \frac{\mathrm{d}\mathbf{i}_0}{\mathrm{d}t}\bigg|_1=-\dot{\varphi}(t)\ \mathbf{j}_0=\mathbf{\omega}_{01}\times\mathbf{i}_0\end{array}\right\}$ $\Rightarrow$ $\mathbf{\omega}_{01}=-\dot{\varphi}(t)\ \mathbf{k}_1$

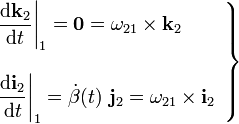
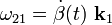
$\left.\begin{array}{l}\displaystyle \frac{\mathrm{d}\mathbf{k}_2}{\mathrm{d}t}\bigg|_1=\mathbf{0}=\mathbf{\omega}_{21}\times\mathbf{k}_2 \\{}\\ \displaystyle \frac{\mathrm{d}\mathbf{i}_2}{\mathrm{d}t}\bigg|_1=\dot{\beta}(t)\ \mathbf{j}_2=\mathbf{\omega}_{21}\times\mathbf{i}_2\end{array}\right\}$ $\Rightarrow$ $\mathbf{\omega}_{21}=\dot{\beta}(t)\ \mathbf{k}_1$

2.1 Determinación gráfica de los C.I.R.

Por tratarse de movimientos planos, los C.I.R. se corresponden con los puntos que en un determinado instante se encuentran en reposo (instantáneo o permanente). Consideremos el instante arbitrario $t$ , en que los ejes $A X 2$ y $C X 0$ forman sendos ángulos $β(t)$ y $\varphi (t)$ .

El sólido “0” (disco) rueda sin deslizar sobre el eje $O X 1$ ; por tanto, si $B$ es el punto de contacto entre ambos sólidos en el instante considerado, tendrá velocidad instantánea nula y sera el C.I.R. del movimiento {01}:

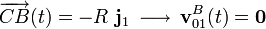
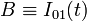
$\overrightarrow{CB}(t)=-R\ \mathbf{j}_1\, \longrightarrow\, \mathbf{v}_{01}^B(t)=\mathbf{0}$ $\Rightarrow$ $B\equiv I_{01}(t)$

El punto $C$ es, en todo instante, el centro del disco “0” y uno de los extremos de la varilla “2”. Por tanto, se trata de un punto que, en todo instante, permanece fijo en el movimiento relativo {20} (y en el {20}, claro). En consecuencia, el centro permanente de rotación de dicho movimiento:

$\mathbf{v}_{20}^C(t)=\mathbf{0}\mathrm{,}\, \forall\ t$ $\Rightarrow$ $C\equiv I_{20}$

@@ Línea 27: / Línea 27: @@
 El sólido &ldquo;0&rdquo; (disco) rueda sin deslizar sobre el eje <math>OX_1</math>; por tanto, si <math>B</math> es el punto de contacto entre ambos sólidos en el instante considerado, tendrá velocidad instantánea nula y sera el C.I.R. del movimiento {01}:
-<center><math>\overrightarrow{CB}(t)=-R\ \mathbf{j}_1\, \longrightarrow\, \mathbf{v}_{01}^B(t)=\mathbf{0}</math>&nbsp; {{tose}} &nbsp;<math style="border:solid blue 2px;padding:10px">B\equiv I_{01}(t)</math></center>
+<center><math>\overrightarrow{CB}(t)=-R\ \mathbf{j}_1\, \longrightarrow\, \mathbf{v}_{01}^B(t)=\mathbf{0}</math>&nbsp; {{tose}} &nbsp;<math style="border:solid blue 2px;padding:10px">B\equiv I_{01}(t)</math></center>[[Imagen:figura2.gif|right]]
 El punto <math>C</math> es, en todo instante, el centro del disco &ldquo;0&rdquo; y uno de los extremos de la varilla &ldquo;2&rdquo;. Por tanto, se trata de un punto que, en todo instante, permanece fijo en el movimiento relativo {20} (y en el {20}, claro). En consecuencia, el ''centro permanente de rotación'' de dicho movimiento:
 <center><math>\mathbf{v}_{20}^C(t)=\mathbf{0}\mathrm{,}\, \forall\ t</math>&nbsp; {{tose}} &nbsp;<math style="border:solid purple 2px;padding:10px">C\equiv I_{20}</math></center>

Disco arrastrando una varilla

De Laplace

Revisión de 15:06 3 feb 2010

1 Enunciado

2 Solución

2.1 Determinación gráfica de los C.I.R.

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES