Disco arrastrando una varilla
De Laplace
(Diferencias entre revisiones)
(→Solución) |
(→Enunciado) |
||
| Línea 4: | Línea 4: | ||
| | ||
| - | En el sistema de la figura los tres sólidos realizan un movimiento plano cuando el disco de radio <math>R</math> (sólido “0”) rueda sin deslizar sobre el sólido “1”. El centro del disco, <math>C</math>, se desplaza con una velocidad <math>\mathbf{v}_C=v(t)\mathbf{i}_1</math>. La barra de longitud <math>3R</math> (sólido “2”) tiene su extremo <math>C</math> articulado en el centro del disco, mientras que se apoya en el borde <math>O</math> del sólido “1”. | + | En el sistema de la figura los tres sólidos realizan un movimiento plano cuando el disco de radio <math>R</math> (sólido “0”) rueda sin deslizar sobre el sólido “1”. El centro del disco, <math>C</math>, se desplaza con una velocidad <math>\mathbf{v}_C=v(t)\mathbf{i}_1</math>. La barra de longitud <math>3R</math> (sólido “2”) tiene su extremo <math>C</math> articulado en el centro del disco, mientras que se apoya en el borde <math>O</math> del sólido “1”. [[Imagen:figura1.gif|left]] |
# Determine gráficamente la posición de los C.I.R. de los movimientos {21}, {20} y {01}. | # Determine gráficamente la posición de los C.I.R. de los movimientos {21}, {20} y {01}. | ||
# En el instante en que la distancia entre los puntos <math>O</math> y <math>B</math> es igual a <math>R</math>, la velocidad del punto <math>C</math> es <math>\mathbf{v}_C=v_0\ \mathbf{i}_1</math>. Calcule las reducciones cinemáticas de los tres movimientos en el punto <math>C</math>. | # En el instante en que la distancia entre los puntos <math>O</math> y <math>B</math> es igual a <math>R</math>, la velocidad del punto <math>C</math> es <math>\mathbf{v}_C=v_0\ \mathbf{i}_1</math>. Calcule las reducciones cinemáticas de los tres movimientos en el punto <math>C</math>. | ||
# Exprese el vector de posición del punto <math>A</math> en el sistema “1”, <math>\mathbf{r}_{21}^A</math>, en función de un ángulo <math>\beta</math> arbitrario. | # Exprese el vector de posición del punto <math>A</math> en el sistema “1”, <math>\mathbf{r}_{21}^A</math>, en función de un ángulo <math>\beta</math> arbitrario. | ||
| - | # Si <math>\dot{\beta}=-\Omega</math>, con <math>\Omega</math> constante y positiva, calcule <math>\mathbf{v}_{21}^A(t)</math> y <math>\mathbf{a}_{21}^A(t)</math> para todo instante de tiempo, en función de <math>\beta</math>, <math>\Omega</math> y <math>R</math>. | + | # Si <math>\dot{\beta}=-\Omega</math>, con <math>\Omega</math> constante y positiva, calcule <math>\mathbf{v}_{21}^A(t)</math> y <math>\mathbf{a}_{21}^A(t)</math> para todo instante de tiempo, en función de <math>\beta</math>, <math>\Omega</math> y <math>R</math>. |
==Solución== | ==Solución== | ||
Revisión de 20:45 2 feb 2010
1 Enunciado
(Primer Parcial, Enero 2010, P1)
En el sistema de la figura los tres sólidos realizan un movimiento plano cuando el disco de radio R (sólido “0”) rueda sin deslizar sobre el sólido “1”. El centro del disco, C, se desplaza con una velocidad
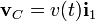. La barra de longitud 3R (sólido “2”) tiene su extremo C articulado en el centro del disco, mientras que se apoya en el borde O del sólido “1”. 
- Determine gráficamente la posición de los C.I.R. de los movimientos {21}, {20} y {01}.
- En el instante en que la distancia entre los puntos O y B es igual a R, la velocidad del punto C es
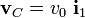. Calcule las reducciones cinemáticas de los tres movimientos en el punto C.
- Exprese el vector de posición del punto A en el sistema “1”,
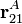, en función de un ángulo β arbitrario.
- Si
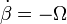, con Ω constante y positiva, calcule 
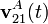y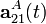 
para todo instante de tiempo, en función de β, Ω y R.
2 Solución
Como paso previo a la solución de los distintos apartados procederemos a adoptar los sistemas de referencia equivalentes a los distintos sólidos rígidos del sistema bajo estudio. En la figura del enunciado se indican los ejes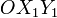 
asocidados al sólido “1”, respecto del cuál, el disco “0” y la varilla “2” realizan sendos movimientos planos {01} y {21}. Además, dichos ejes definen el plano director para estos movimientos.
