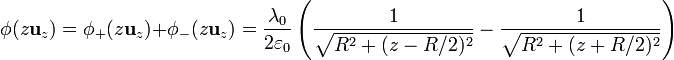Entrar Página Discusión Historial Go to the site toolbox

Campo de dos anillos coaxiales

De Laplace

(Diferencias entre revisiones)
(→Campo de un solo anillo)
(→Potencial de los dos anillos)
Línea 30: Línea 30:
Sumando las dos contribuciones
Sumando las dos contribuciones
-
<math>\phi(z\mathbf{u}_z)=\phi_+(z\mathbf{u}_z)+\phi_-(z\mathbf{u}_z)=\frac{\lambda_0}{2\varepsilon_0}\left(\frac{1}{\sqrt{R^2+(z-R/2)^2}}-\frac{1}{\sqrt{R^2+(z+R/2)^2}}\right)</math>
+
<center><math>\phi(z\mathbf{u}_z)=\phi_+(z\mathbf{u}_z)+\phi_-(z\mathbf{u}_z)=\frac{\lambda_0}{2\varepsilon_0}\left(\frac{1}{\sqrt{R^2+(z-R/2)^2}}-\frac{1}{\sqrt{R^2+(z+R/2)^2}}\right)</math></center>
==Campo eléctrico==
==Campo eléctrico==

Revisión de 20:03 28 ene 2010

Contenido

1 Enunciado

Dos anillos iguales de radio R y grosor despreciable están cargados eléctricamente con sendas distribuciones lineales y uniformes + λ0 y − λ0. Los anillos se encuentran en planos paralelos separados una distancia R, pero con sus centros situados sobre el mismo eje. Tómese este eje como Z, y como origen de coordenadas O el punto medio entre los anillos.
  1. Obtenga la expresión del potencial electrostático creado por estas distribuciones en los puntos del eje Z. Calcule el valor del potencial en un punto arbitrario del plano XY.
  2. Obtenga la expresión del campo eléctrico para los puntos del eje Z. ¿Cuánto vale la fuerza que actúa sobre una carga puntual q situada en O? ¿Qué trabajo se ha realizado para traer esta carga desde el infinito hasta este punto?
  3. Suponga que, en lugar de la carga puntual, se sitúa un dipolo eléctrico de momento dipolar 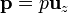\mathbf{p}=p\mathbf{u}_z, en el centro del anillo de carga positiva. Obtenga la expresión de la energía potencial del dipolo y la fuerza que actúa sobre él.
  4. Obtenga los momentos monopolar y dipolar del sistema de dos anillos y proporcione expresiones aproximadas para el potencial eléctrico y el campo eléctrico en puntos alejados del sistema

2 Potencial

Tanto el potencial eléctrico como el campo de dos anillos pueden calcularse mediante el principio de superposición, hallando en primer lugar el potencial de un solo anillo y posteriormente sumando las dos contribuciones.

2.1 Campo de un solo anillo

Consideremos el anillo en z = + R / 2. El potencial que produce en su eje puede hallarse por integración directa, según la expresión

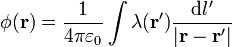
\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \lambda(\mathbf{r}')\frac{\mathrm{d}l'}{|\mathbf{r}-\mathbf{r}'|}

Tenemos que

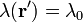
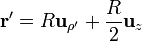
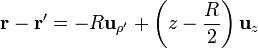
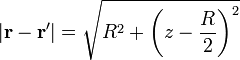
\lambda(\mathbf{r}')=\lambda_0        \mathbf{r}=z\mathbf{u}_z\,        \mathbf{r}'=R\mathbf{u}_{\rho'}+\frac{R}{2}\mathbf{u}_z\,        \mathbf{r}-\mathbf{r}'=-R\mathbf{u}_{\rho'}+\left(z-\frac{R}{2}\right)\mathbf{u}_z\,        |\mathbf{r}-\mathbf{r}'|=\sqrt{R^2+\left(z-\frac{R}{2}\right)^2}        \mathrm{d}l'=|\mathrm{d}\mathbf{r}'|=R\,\mathrm{d}\varphi'

Sustituyendo todo esto queda la integral

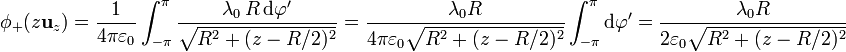
\phi_+(z\mathbf{u}_z)=\frac{1}{4\pi\varepsilon_0}\int_{-\pi}^\pi \frac{\lambda_0\,R\,\mathrm{d}\varphi'}{\sqrt{R^2+(z-R/2)^2}} = \frac{\lambda_0 R}{4\pi\varepsilon_0\sqrt{R^2+(z-R/2)^2}}\int_{-\pi}^\pi \mathrm{d}\varphi'=\frac{\lambda_0 R}{2\varepsilon_0\sqrt{R^2+(z-R/2)^2}}

3 Potencial de los dos anillos

El potencial del segundo anillo es análogo al anterior, sin más que cambiar + λ0 por − λ0 y + R / 2 por − R / 2

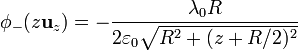
\phi_-(z\mathbf{u}_z)=-\frac{\lambda_0 R}{2\varepsilon_0\sqrt{R^2+(z+R/2)^2}}

Sumando las dos contribuciones

\phi(z\mathbf{u}_z)=\phi_+(z\mathbf{u}_z)+\phi_-(z\mathbf{u}_z)=\frac{\lambda_0}{2\varepsilon_0}\left(\frac{1}{\sqrt{R^2+(z-R/2)^2}}-\frac{1}{\sqrt{R^2+(z+R/2)^2}}\right)

4 Campo eléctrico

5 Fuerza y energía de un dipolo

6 Desarrollo multipolar

Obtenido de "http://tesla.us.es/wiki/index.php/Campo_de_dos_anillos_coaxiales"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace