Potencial de dos cargas puntuales
De Laplace
(Nueva página: ==Enunciado== Halle el potencial creado por dos cargas <math>q_1</math>, <math>-q_2</math> situadas a una distancia <math>a</math> una de la otra. Demuestre que la superficie equipote...) |
(→Solución) |
||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 3: | Línea 3: | ||
==Solución== | ==Solución== | ||
| + | El potencial creado por estas dos cargas en cualquier punto del espacio es | ||
| + | |||
| + | <center><math>\phi(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1}{|\mathbf{r}-\mathbf{r}_1|}-\frac{q_2}{|\mathbf{r}-\mathbf{r}_2|}\right)</math></center> | ||
| + | |||
| + | La equipotencial V=0 vendrá dada por la ecuación | ||
| + | |||
| + | <center><math>\frac{1}{4\pi\varepsilon_0}\left(\frac{q_1}{|\mathbf{r}-\mathbf{r}_1|}-\frac{q_2}{|\mathbf{r}-\mathbf{r}_2|}\right)=0</math></center> | ||
| + | |||
| + | No es evidente que ésta sea la ecuación de una esfera. Para ponerlo de manifiesto reescribimos la ecuación como | ||
| + | |||
| + | <center><math>\left|\mathbf{r}-\mathbf{r}_2\right|=\gamma \left|\mathbf{r}-\mathbf{r}_1\right|</math>{{qquad}}<math>\gamma=\frac{q_2}{q_1}</math></center> | ||
| + | |||
| + | Supondremos, sin pérdida de generalidad, que <math>\gamma < 1</math>, esto es, que <math>q_2</math> es la menor en magnitud de las dos cargas. | ||
| + | |||
| + | Podemos tomar el origen de coordenadas en la carga <math>q_1</math> y el eje Z el que pasa por las dos cargas, de forma que <math>\mathbf{r}_2=a\mathbf{u}_z</math>. Expresando el vector de posición en cartesianas esta ecuación queda | ||
| + | |||
| + | <center><math>\sqrt{x^2+y^2+(z-a)^2}=\gamma \sqrt{x^2+y^2+z^2}</math></center> | ||
| + | |||
| + | Elevando al cuadrado y agrupando términos | ||
| + | |||
| + | <center><math>\left(x^2+y^2+z^2\right)\left(1-\gamma^2\right)-2za + a^2 = 0</math></center> | ||
| + | |||
| + | Esta es ya claramente la ecuación de una esfera. Para identificar su radio y la posición del centro, despejamos y competamos cuadrados | ||
| + | |||
| + | <center><math>x^2+y^2+z^2-2z\frac{a}{1-\gamma^2} + \frac{a^2}{1-\gamma^2} = 0</math></center> | ||
| + | |||
| + | <center><math>x^2+y^2+\left(z-\frac{a}{1-\gamma^2}\right)^2 = \frac{a^2}{(1-\gamma^2)^2}-\frac{a^2}{1-\gamma^2}=\frac{a^2\gamma^2}{(1-\gamma^2)^2}</math></center> | ||
| + | |||
| + | [[Imagen:potencial2cargasb.png|267px|right]]De aquí obtenemos el radio y el centro de la esfera | ||
| + | |||
| + | <center><math>R = \frac{a\gamma}{1-\gamma^2}</math>{{qquad}}{{qquad}}<math>\mathbf{C}=\frac{a\mathbf{u}_z}{1-\gamma^2}</math></center> | ||
| + | |||
| + | * Dado que <math>\mathbf{C}\neq \mathbf{0}</math> y <math>\mathbf{C}\neq \mathbf{r}_2</math>, la esfera no está centrada en ninguna de las dos cargas | ||
| + | |||
| + | * Puesto que <math>|\mathbf{C}|-R < a < |\mathbf{C}|+R</math>, esta esfera envuelve a la menor de las dos cargas, aunque no está centrada en ella. | ||
| + | |||
| + | * Sólo la equipotencial <math>V=0</math> es una esfera. El resto de las equipotenciales tienen formas más complicadas, no esféricas. | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
última version al 20:22 13 ene 2010
1 Enunciado
Halle el potencial creado por dos cargas q1, − q2 situadas a una distancia a una de la otra. Demuestre que la superficie equipotencial V = 0 es una esfera.
2 Solución
El potencial creado por estas dos cargas en cualquier punto del espacio es
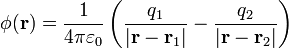
La equipotencial V=0 vendrá dada por la ecuación
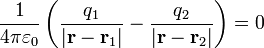
No es evidente que ésta sea la ecuación de una esfera. Para ponerlo de manifiesto reescribimos la ecuación como

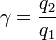
Supondremos, sin pérdida de generalidad, que γ < 1, esto es, que q2 es la menor en magnitud de las dos cargas.
Podemos tomar el origen de coordenadas en la carga q1 y el eje Z el que pasa por las dos cargas, de forma que 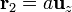 . Expresando el vector de posición en cartesianas esta ecuación queda
. Expresando el vector de posición en cartesianas esta ecuación queda
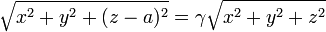
Elevando al cuadrado y agrupando términos

Esta es ya claramente la ecuación de una esfera. Para identificar su radio y la posición del centro, despejamos y competamos cuadrados
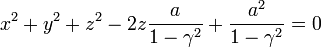
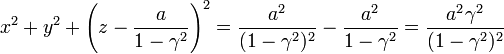
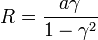
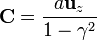
- Dado que
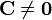 y
y 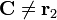 , la esfera no está centrada en ninguna de las dos cargas
, la esfera no está centrada en ninguna de las dos cargas
- Puesto que
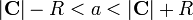 , esta esfera envuelve a la menor de las dos cargas, aunque no está centrada en ella.
, esta esfera envuelve a la menor de las dos cargas, aunque no está centrada en ella.
- Sólo la equipotencial V = 0 es una esfera. El resto de las equipotenciales tienen formas más complicadas, no esféricas.






