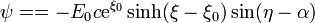Entrar Página Discusión Historial Go to the site toolbox

Partícula elíptica en campo eléctrico oblicuo

De Laplace

(Diferencias entre revisiones)
(→Solución para el potencial)
(→Solución para el potencial)
Línea 56: Línea 56:
<center><math>\phi= -E_0c\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)\cos(\eta-\alpha)</math></center>
<center><math>\phi= -E_0c\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)\cos(\eta-\alpha)</math></center>
 +
 +
mientras que la función corriente, que nos da las líneas de campo, es
 +
 +
<center><math>\psi = = -E_0c\mathrm{e}^{\xi_0}\sinh(\xi-\xi_0)\sin(\eta-\alpha)</math></center>
==Momento dipolar==
==Momento dipolar==
==Torque==
==Torque==

Revisión de 19:56 12 ene 2010

Contenido

1 Planteamiento

Tenemos una elipse de semiejes a y b (a > b) recubierta de una capa doble. La partícula está sometida a un campo eléctrico que en el infinito es uniforme y forma un ángulo α con el semieje mayor.

El problema del potencial se convierte en la solución de la ecuación de Laplace

\nabla^2\phi = 0

con la condición de Neumann en la superficie de la partícula

\mathbf{n}\cdot\nabla\phi = 0\qquad(\mathbf{r}\in S)

y con el comportamiento asintótico

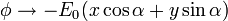
\phi\to -E_0(x\cos\alpha+y\sin\alpha)\,

2 Coordenadas elípticas

Para resolver el problema eléctrico empleamos las coordenadas elípticas definidas por

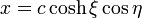
x = c \cosh\xi\cos\eta\,        y = c \sinh\xi\sin\eta\,

con

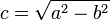
c = \sqrt{a^2-b^2}

En estas coordenadas la superficie de la elipse viene definida por

\xi=\xi_0=\,\mathrm{arctanh}\left(\frac{b}{a}\right)

Para estas coordenadas tenemos los factores de escala

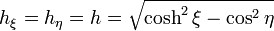
h_\xi = h_\eta = h = \sqrt{\cosh^2\xi-\cos^2\eta}

Al ser iguales, la ecuación de Laplace preseva su forma, de manera que hay que resolver

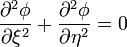
\frac{\partial^2\phi}{\partial\xi^2}+\frac{\partial^2\phi}{\partial\eta^2}=0

con la condición de Neumann

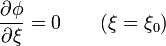
\frac{\partial\phi}{\partial\xi}=0\qquad(\xi=\xi_0)\,

y con la condición de que en el infinito

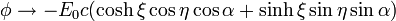
\phi\to-E_0c(\cosh\xi\cos\eta\cos\alpha+\sinh\xi\sin\eta\sin\alpha)\,

3 Solución para el potencial

La solución se halla simplemente observando que la condición de que a grandes distancias

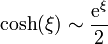
\cosh(\xi)\sim \frac{\mathrm{e}^\xi}{2}         \sinh(\xi)\sim \frac{\mathrm{e}^\xi}{2}

lo que nos permite sustituir el potencial en el infinito por

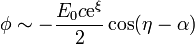
\phi\sim -\frac{E_0c\mathrm{e}^{\xi}}{2}\cos(\eta-\alpha)

y esta, que ya es de por sí una solución de la ecuación de Laplace, nos dice cual es la solución del problema completo (que en 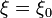\xi = \xi_0\, tiene derivada nula). El potencial es

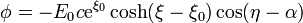
\phi= -E_0c\mathrm{e}^{\xi_0}\cosh(\xi-\xi_0)\cos(\eta-\alpha)

mientras que la función corriente, que nos da las líneas de campo, es

\psi = = -E_0c\mathrm{e}^{\xi_0}\sinh(\xi-\xi_0)\sin(\eta-\alpha)

4 Momento dipolar

5 Torque

Obtenido de "http://tesla.us.es/wiki/index.php/Part%C3%ADcula_el%C3%ADptica_en_campo_el%C3%A9ctrico_oblicuo"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace