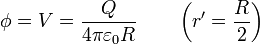Esfera con hueco relleno de carga
De Laplace
(→Exterior del conductor) |
(→Exterior del conductor) |
||
| Línea 22: | Línea 22: | ||
La [[Capacidad_de_una_esfera|solución de este problema]] es conocida: | La [[Capacidad_de_una_esfera|solución de este problema]] es conocida: | ||
| - | <center><math>\phi = \frac{VR}{r}</math>{{qquad}}{{qquad}}<math>\mathbf{E}=\frac{VR}{r^2}\mathbf{u}_r\qquad(r>R)</math></center> | + | <center><math>\phi = \frac{VR}{r}</math>{{qquad}}{{qquad}}<math>\mathbf{E}=-\nabla\phi=\frac{VR}{r^2}\mathbf{u}_r\qquad(r>R)</math></center> |
El valor de <math>V</math> lo obtenemos a partir de la carga. Si consideramos el flujo de <math>\mathbf{E}</math> a través una superficie esférica que envuelva a la esfera conductora, la ley de Gauss nos da la carga encerrada | El valor de <math>V</math> lo obtenemos a partir de la carga. Si consideramos el flujo de <math>\mathbf{E}</math> a través una superficie esférica que envuelva a la esfera conductora, la ley de Gauss nos da la carga encerrada | ||
| Línea 35: | Línea 35: | ||
<center><math>\phi = \frac{Q}{4\pi\varepsilon_0 r}</math>{{qquad}}{{qquad}}<math>\mathbf{E}=\frac{Q}{4\pi\varepsilon_0 r^2}\mathbf{u}_r\qquad (r>R)</math></center> | <center><math>\phi = \frac{Q}{4\pi\varepsilon_0 r}</math>{{qquad}}{{qquad}}<math>\mathbf{E}=\frac{Q}{4\pi\varepsilon_0 r^2}\mathbf{u}_r\qquad (r>R)</math></center> | ||
| + | |||
| + | Esto se corresponde con el que en un conductor a carga fijada, con un hueco, un observador exterior es capaz de apreciar la magnitud de la carga, pero no su distribución en el interior o siquiera la existencia del hueco. Solo ve una distribución de carga uniforme en la superficie exterior del conductor. | ||
| + | |||
| + | ===Material conductor=== | ||
| + | Por estar en equilibrio electrostático, el material conductor es equipotencial y el valor del potencial es el que acabamos de calcular | ||
| + | |||
| + | <center><math>\phi = V = \frac{Q}{4\pi\varepsilon_0r}</math>{{qquad}}{{qquad}}<math>\mathbf{E}==-\nabla\phi=\mathbf{0}\qquad(\mathbf{r}\in\tau)</math></center> | ||
| + | |||
| + | siendo <math>\tau</math> el volumen del material conductor | ||
| + | |||
| + | ===Hueco del conductor=== | ||
| + | Puesto que el hueco no está centrado en la esfera metálica, llamemos <math>r'</math> a la coordenada radial medida desde el centro del hueco. | ||
| + | |||
| + | En este caso el problema del potencial no verifica la ecuación de Laplace, sino la de Poisson | ||
| + | |||
| + | <center><math>\nabla^2\phi = -\frac{\rho}{\varepsilon_0}\qquad \left(r'<\frac{R}{2}\right)</math></center> | ||
| + | |||
| + | con la condición de contorno de que la pared del hueco es parte del conductor | ||
| + | |||
| + | <center><math>\phi = V = \frac{Q}{4\pi\varepsilon_0R}\qquad\left(r'=\frac{R}{2}\right)</math></center> | ||
==Conductor a tensión ''V''<sub>0</sub>== | ==Conductor a tensión ''V''<sub>0</sub>== | ||
==Carga suministrada== | ==Carga suministrada== | ||
[[Categoría:Problemas de electrostática en presencia de conductores]] | [[Categoría:Problemas de electrostática en presencia de conductores]] | ||
Revisión de 23:11 10 ene 2010
Contenido |
1 Enunciado
Una esfera conductora de radio R tiene un hueco, también esférico, de radio R / 2, no siendo el hueco concéntrico con la esfera (sea a la distancia entre centros). Inicialmente la esfera se encuentra aislada y descargada.
- Obtenga las expresiones del campo eléctrico y del potencial en todos los puntos del espacio cuando en el hueco se introduce una carga Q0 distribuida uniformemente en el volumen del hueco.
- Manteniendo esta carga en el hueco, la superficie de la esfera conductora se conecta a una fuente de potencial de valor V0. ¿Cuánto valen el campo y el potencial en todo el espacio una vez que se alcanza el equilibrio electrostático?
- ¿Cuánta carga aporta el generador en el paso anterior?
2 Conductor descargado
Tenemos tres regiones: el hueco, el material conductor, y el exterior de la esfera conductora. El campo y el potencial en cada una son:
2.1 Exterior del conductor
Desde fuera del conductor solo vemos una esfera, de radio R en equilibrio electrostático. El problema del potencial, en esta región exterior es
con las condiciones de contorno
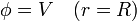
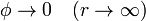
siendo V el potencial de la esfera, cuyo valor desconocemos por ahora y que calcularemos más tarde.
La solución de este problema es conocida:
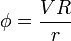
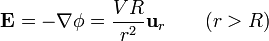
El valor de V lo obtenemos a partir de la carga. Si consideramos el flujo de 
a través una superficie esférica que envuelva a la esfera conductora, la ley de Gauss nos da la carga encerrada
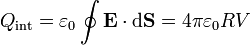
Por otro lado, la carga encerrada es solo la del hueco, pues el conductor está descargado. Por ello
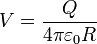
y el potencial y el campo en el exterior son
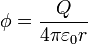
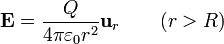
Esto se corresponde con el que en un conductor a carga fijada, con un hueco, un observador exterior es capaz de apreciar la magnitud de la carga, pero no su distribución en el interior o siquiera la existencia del hueco. Solo ve una distribución de carga uniforme en la superficie exterior del conductor.
2.2 Material conductor
Por estar en equilibrio electrostático, el material conductor es equipotencial y el valor del potencial es el que acabamos de calcular
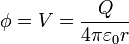
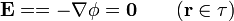
siendo τ el volumen del material conductor
2.3 Hueco del conductor
Puesto que el hueco no está centrado en la esfera metálica, llamemos r' a la coordenada radial medida desde el centro del hueco.
En este caso el problema del potencial no verifica la ecuación de Laplace, sino la de Poisson
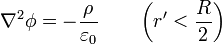
con la condición de contorno de que la pared del hueco es parte del conductor
