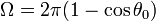Flujo del campo eléctrico de una carga
De Laplace
(→En cilíndricas) |
(→En esféricas) |
||
| (8 ediciones intermedias no se muestran.) | |||
| Línea 2: | Línea 2: | ||
Halle el flujo del campo eléctrico debido a una carga puntual <math>q</math> a través de un disco cuyo eje pasa por el punto donde se encuentra la carga. | Halle el flujo del campo eléctrico debido a una carga puntual <math>q</math> a través de un disco cuyo eje pasa por el punto donde se encuentra la carga. | ||
| - | El disco tiene radio <math> | + | El disco tiene radio <math>a</math> y la distancia de la carga al plano del disco es <math>h</math>. |
# Utilizando coordenadas cilíndricas | # Utilizando coordenadas cilíndricas | ||
| Línea 19: | Línea 19: | ||
==En cilíndricas== | ==En cilíndricas== | ||
| - | + | Situamos, según hemos dicho, el origen de coordenadas sobre la carga puntual, y el eje Z como el eje del disco. De esta forma, el disco queda parametrizado como | |
| - | <center><math>z=h\,</math>{{qquad}}<math>\rho\in[0, | + | <center><math>z=h\,</math>{{qquad}}<math>\rho\in[0,a]</math>{{qquad}}{{qquad}}<math>\varphi\in[0,2\pi)</math></center> |
El vector de posición de los puntos del disco y el vector diferencial de superficie valen | El vector de posición de los puntos del disco y el vector diferencial de superficie valen | ||
<center><math> | <center><math> | ||
| - | \mathbf{r}=\rho\mathbf{u}_\rho+h\mathbf{u}_z\,</math>{{qquad}}{{qquad}}<math>r=\sqrt{h^2+\rho^2}</math>{{qquad}}{{qquad}}<math>\mathrm{d}\mathbf{S}=\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi\,\mathbf{u}_z</math>{{qquad}} | + | \mathbf{r}=\rho\mathbf{u}_\rho+h\mathbf{u}_z\,</math>{{qquad}}{{qquad}}<math>r=\sqrt{h^2+\rho^2}</math>{{qquad}}{{qquad}}<math>\mathrm{d}\mathbf{S}=\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi\,\mathbf{u}_z</math>{{qquad}}{{qquad}}<math>\mathbf{r}\cdot\mathrm{d}\mathbf{S}=h\,\rho\,\mathrm{d}\rho\,\mathrm{d}\varphi</math></center> |
Sustituimos en la expresión del flujo | Sustituimos en la expresión del flujo | ||
| - | <center><math>\Phi_\mathrm{e}=\frac{q}{4\pi\varepsilon_0}\int_{0}^{2\pi}\!\!\mathrm{d}\varphi\int_0^ | + | <center><math>\Phi_\mathrm{e}=\frac{q}{4\pi\varepsilon_0}\int_{0}^{2\pi}\!\!\mathrm{d}\varphi\int_0^a\!\!\mathrm{d}\rho\frac{h\rho}{(\rho^2+h^2)^{3/2}}</math></center> |
La primera integral produce un factor <math>2\pi</math>, mientras que la segunda es casi inmediata | La primera integral produce un factor <math>2\pi</math>, mientras que la segunda es casi inmediata | ||
| - | <center><math>\Phi_\mathrm{e} = \frac{qh}{2\varepsilon_0}\left(-\frac{1}{\sqrt{\rho^2+h^2}\right|_0^ | + | <center><math>\Phi_\mathrm{e} = \frac{qh}{2\varepsilon_0}\left.\left(-\frac{1}{\sqrt{\rho^2+h^2}}\right)\right|_0^a = \frac{qh}{2\varepsilon_0}\left(\frac{1}{h}-\frac{1}{\sqrt{a^2+h^2}}\right) = \frac{q}{\varepsilon_0}\,\frac{1-\cos\theta_0}{2}</math></center> |
donde | donde | ||
| - | <center><math>\cos\theta_0=\frac{h}{\sqrt{h^2+ | + | <center><math>\cos\theta_0=\frac{h}{\sqrt{h^2+a^2}}</math></center> |
siendo <math>\theta_0</math> el ángulo con el que se ve el borde del disco desde el origen de coordenadas. | siendo <math>\theta_0</math> el ángulo con el que se ve el borde del disco desde el origen de coordenadas. | ||
==En esféricas== | ==En esféricas== | ||
| + | El cálculo del flujo a través del disco lo podemos hallar igualmente empleando coordenadas esféricas. Sin embargo, se plantea el problema de cómo se expresa el diferencial de superficie <math>z=h=\mathrm{cte}</math> en coordenadas esféricas, pues en este sistema no se trata de una superficie coordenada. | ||
| + | |||
| + | Afortunadamente, no necesitamos resolver esa cuestión. Según indicamos, el flujo del campo eléctrico de una carga puntual a través de una superficie cualquiera es | ||
| + | |||
| + | <center><math>\Phi_\mathrm{e}=\frac{q}{\varepsilon_0}\,\frac{\Omega}{4\pi}</math></center> | ||
| + | |||
| + | y el ángulo sólido abarcado por una superficie <math>S</math> sólo depende del borde de dicha superficie. Cualquier otra superficie <math>S'</math> apoyada en la misma curva <math>\Gamma</math> y orientada en el mismo sentido producirá la misma proyección sobre una esfera de radio <math>a</math> centrada en la carga y por tanto abarcará el mismo ángulo sólido. | ||
| + | |||
| + | Así pues lo que necesitamos es una superficie sencilla en coordenadas esféricas cuyo borde sea un anillo de radio <math>R</math> situado a una altura <math>h</math>. Esta superficie es un casquete esférico apoyado en dicho anillo. | ||
| + | |||
| + | Este casquete se puede parametrizar como | ||
| + | |||
| + | <center> | ||
| + | <math>\mathbf{r}=R\mathbf{u}_r</math>{{qquad}}{{qquad}}<math>R = \sqrt{a^2+h^2}</math>{{qquad}}{{qquad}}<math>\theta\in[0,\theta_0]</math>{{qquad}}{{qquad}}<math>\varphi\in[0,2\pi)</math>{{qquad}}{{qquad}}<math>\mathrm{d}\mathbf{S}=R^2\,\mathrm{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi\,\mathbf{u}_r</math>{{qquad}}{{qquad}}<math>\mathbf{r}\cdot\mathrm{d}\mathbf{S}=R^3\,\mathrm{sen}\,\theta\,\mathrm{d}\theta\,\mathrm{d}\varphi</math></center> | ||
| + | |||
| + | Obsérvese que los límite de variación de la coordenadas esférica <math>\theta</math> son 0 (el cenit de la carga) y <math>\theta_0</math>, definido anteriormente como el ángulo con el que se ve el borde. | ||
| + | |||
| + | Sustituyendo en la expresión del flujo del campo eléctrico | ||
| + | |||
| + | <center><math>\Phi_\mathrm{e}=\frac{q}{4\pi\varepsilon_0}\int_0^{2\pi}\!\!\mathrm{d}\varphi\int_0^{\theta_0}\!\!\mathrm{d}\theta\frac{R^3\,\mathrm{sen}\,\theta}{R^3}=\frac{q}{\varepsilon_0}\,\frac{1-\cos\theta_0}{2}</math></center> | ||
| + | |||
| + | El resultado, naturalmente, coincide con el anterior. Vemos también que el ángulo sólido abarcado por un casquete esférico es | ||
| + | |||
| + | <center><math>\Omega = 2\pi(1-\cos\theta_0)\,</math></center> | ||
| + | |||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
última version al 11:16 9 ene 2010
Contenido |
1 Enunciado
Halle el flujo del campo eléctrico debido a una carga puntual q a través de un disco cuyo eje pasa por el punto donde se encuentra la carga.
El disco tiene radio a y la distancia de la carga al plano del disco es h.
- Utilizando coordenadas cilíndricas
- Usando coordenadas esféricas (Sugerencia: En lugar del disco emplee otra superficie que abarque el mismo ángulo sólido).
2 Introducción
El flujo del campo eléctrico de una carga puntual (sobre la cual, por comodidad, situamos el origen de coordenadas) es
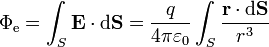
La integral que aparece en el último miembro no es más que el ángulo sólido, Ω, abarcado por la superficie, vista desde el origen de coordenadas. Por tanto
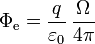
El problema se reduce, por tanto, a determinar el ángulo sólido con el que el disco se ve desde la carga.
3 En cilíndricas
Situamos, según hemos dicho, el origen de coordenadas sobre la carga puntual, y el eje Z como el eje del disco. De esta forma, el disco queda parametrizado como
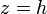
![\rho\in[0,a]](/wiki/images/math/1/4/c/14cffb3eabfaf2ff246e2cc2b8036fe7.png)
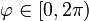
El vector de posición de los puntos del disco y el vector diferencial de superficie valen
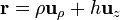
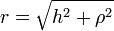
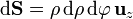
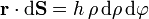
Sustituimos en la expresión del flujo
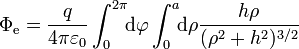
La primera integral produce un factor 2π, mientras que la segunda es casi inmediata
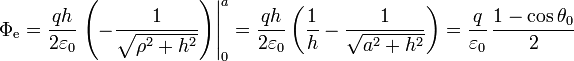
donde
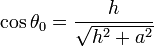
siendo θ0 el ángulo con el que se ve el borde del disco desde el origen de coordenadas.
4 En esféricas
El cálculo del flujo a través del disco lo podemos hallar igualmente empleando coordenadas esféricas. Sin embargo, se plantea el problema de cómo se expresa el diferencial de superficie z = h = cte en coordenadas esféricas, pues en este sistema no se trata de una superficie coordenada.
Afortunadamente, no necesitamos resolver esa cuestión. Según indicamos, el flujo del campo eléctrico de una carga puntual a través de una superficie cualquiera es
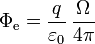
y el ángulo sólido abarcado por una superficie S sólo depende del borde de dicha superficie. Cualquier otra superficie S' apoyada en la misma curva Γ y orientada en el mismo sentido producirá la misma proyección sobre una esfera de radio a centrada en la carga y por tanto abarcará el mismo ángulo sólido.
Así pues lo que necesitamos es una superficie sencilla en coordenadas esféricas cuyo borde sea un anillo de radio R situado a una altura h. Esta superficie es un casquete esférico apoyado en dicho anillo.
Este casquete se puede parametrizar como
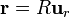
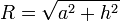
![\theta\in[0,\theta_0]](/wiki/images/math/a/0/3/a0351909e3d4ebed3b089dbc3dd361de.png)
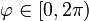
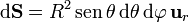
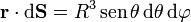
Obsérvese que los límite de variación de la coordenadas esférica θ son 0 (el cenit de la carga) y θ0, definido anteriormente como el ángulo con el que se ve el borde.
Sustituyendo en la expresión del flujo del campo eléctrico
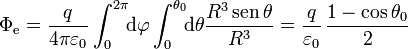
El resultado, naturalmente, coincide con el anterior. Vemos también que el ángulo sólido abarcado por un casquete esférico es