Flujo del campo eléctrico de una carga
De Laplace
(Diferencias entre revisiones)
(→Introducción) |
(→Introducción) |
||
| Línea 10: | Línea 10: | ||
El flujo del campo eléctrico de una carga puntual (sobre la cual, por comodidad, situamos el origen de coordenadas) es | El flujo del campo eléctrico de una carga puntual (sobre la cual, por comodidad, situamos el origen de coordenadas) es | ||
| - | <center><math>\ | + | <center><math>\Phi_\mathrm{e} = \int_S \mathbf{E}\cdot\mathrm{d}\mathbf{S}=\frac{q}{4\pi\varepsilon_0}\int_S\frac{\mathbf{r}\cdot\mathrm{d}\mathbf{S}}{r^3}</math></center> |
La integral que aparece en el último miembro no es más que el [[ángulo sólido]], <math>\Omega</math>, abarcado por la superficie, vista desde el origen de coordenadas. Por tanto | La integral que aparece en el último miembro no es más que el [[ángulo sólido]], <math>\Omega</math>, abarcado por la superficie, vista desde el origen de coordenadas. Por tanto | ||
| - | <center><math>\ | + | <center><math>\Phi_\mathrm{e} = \frac{q}{\varepsilon_0}\,\frac{\Omega}{4\pi}</math></center> |
| + | |||
| + | El problema se reduce, por tanto, a determinar el ángulo sólido con el que el disco se ve desde la carga. | ||
==En cilíndricas== | ==En cilíndricas== | ||
==En esféricas== | ==En esféricas== | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
Revisión de 10:08 9 ene 2010
Contenido |
1 Enunciado
Halle el flujo del campo eléctrico debido a una carga puntual q a través de un disco cuyo eje pasa por el punto donde se encuentra la carga.
El disco tiene radio R y la distancia de la carga al plano del disco es h.
- Utilizando coordenadas cilíndricas
- Usando coordenadas esféricas (Sugerencia: En lugar del disco emplee otra superficie que abarque el mismo ángulo sólido).
2 Introducción
El flujo del campo eléctrico de una carga puntual (sobre la cual, por comodidad, situamos el origen de coordenadas) es
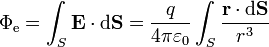
La integral que aparece en el último miembro no es más que el ángulo sólido, Ω, abarcado por la superficie, vista desde el origen de coordenadas. Por tanto
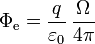
El problema se reduce, por tanto, a determinar el ángulo sólido con el que el disco se ve desde la carga.





