Entrar Página Discusión Historial Go to the site toolbox

Caso extremo de ciclo Diesel

De Laplace

(Diferencias entre revisiones)
(→Valores numéricos)
(→Valores numéricos)
Línea 129: Línea 129:
Reuniendo todos estos resultados en una tabla nos queda
Reuniendo todos estos resultados en una tabla nos queda
-
{|class="bordeado"
+
<center>{|class="bordeado"
|-
|-
!
!
Línea 151: Línea 151:
| 1350
| 1350
|-
|-
-
|}
+
|}</center>
==Entropía==
==Entropía==
==Trabajo perdido==
==Trabajo perdido==
[[Categoría:Problemas del segundo principio de la termodinámica]]
[[Categoría:Problemas del segundo principio de la termodinámica]]

Revisión de 18:49 15 jun 2009

Contenido

1 Enunciado

Una máquina térmica funciona funciona con aire (gas ideal) según el siguiente proceso:

  • El gas contenido en una cámara se comprime adiabáticamente de forma reversible desde un volumen máximo VA hasta un volumen VB, siendo la razón de compresión r = VA / VB.
  • A partir de ahí, el gas se pone en contacto con un foco térmico y se calienta a presión constante hasta un estado C, cuyo volumen es igual al inicial.
  • Acto seguido, el gas se enfría a volumen constante hasta que la temperatura retorna a su valor inicial.
  1. Halle el calor absorbido y cedido por el gas durante el ciclo, así como el trabajo realizado sobre el sistema. Demuestre que el rendimiento de este ciclo es igual a
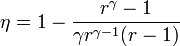
\eta = 1 - \frac{r^\gamma-1}{\gamma r^{\gamma-1}(r-1)}
  1. Para el caso concreto de aire con 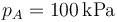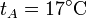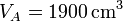p_A=100\,\mathrm{kPa}, t_A=17^\circ\mathrm{C}, V_A=1900\,\mathrm{cm}^3 y r = 3, ¿cuánto valen las temperaturas y presiones en B y C? ¿Y el calor absorbido, el cedido y el trabajo realizado? ¿Y el rendimiento?
  2. Supongamos que el calentamiento se produce a base de poner en contacto el gas con un foco a temperatura constante TC, y el enfriamiento mediante el contacto con el ambiente a TA. ¿Cuánto vale la variación de entropía en el sistema y en el universo en cada paso? ¿Cuál es la variación neta de entropía del universo?
  3. ¿Cuánto vale el trabajo perdido en este ciclo si lo comparamos con el máximo posible para el mismo calor absorbido con las temperaturas de trabajo TA y TC?

2 Calor, trabajo y rendimiento

2.1 Calor absorbido

De los tres procesos que tienen lugar en el ciclo en uno de ellos, la compresión adiabática, no se intercambia calor; en otro, el calentamiento isóbara, el sistema absorbe calor, y en el tercero, el enfriamiento isócoro, el sistema cede calor.

Al ser el proceso de calentamiento uno a presión constante entre las temperaturas TB y TC, el calor absorbido es

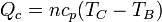
Q_c = nc_p(T_C-T_B)\,

2.2 Calor cedido

El calor se cede en un proceso a volumen constante, entre las temperaturas TC y TA, por lo que vale

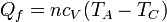
Q_f = nc_V(T_A-T_C)\,

puesto que TA < TC, este calor es negativo, como corresponde a que este calor sale del sistema hacia el ambiente.

2.3 Trabajo

Podemos calcular el valor neto del trabajo realizado sobre el sistema empleando el Primer Principio de la termodinámica, ya que en un proceso cíclico la energía interna al final es la misma que al principio

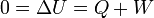
0 = \Delta U = Q+W\,    \Rightarrow    W = -Q = -Q_c-Q_f = -nc_p(T_C-T_B)-nc_V(T_A-T_C)\,

Podemos calcular este valor a partir del trabajo realizado sobre el sistema en cada proceso:

Compresión adiabática
En este proceso no se intercambia calor, por lo que el trabajo es igual al incremento de energía interna
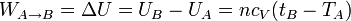
W_{A\to B}=\Delta U = U_B-U_A = nc_V(t_B-T_A)\,
Calentamiento a presión constante
El trabajo cuando la presión es constante es igual a esta presión por el incremento de volumen, cambiado de signo
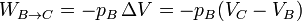
W_{B\to C}=-p_B\,\Delta V = -p_B(V_C - V_B)\,
Podemos poner esto en función de la temperatura, usando la ecuación de los gases ideales
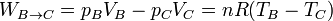
W_{B\to C}= p_BV_B-p_CV_C=nR(T_B-T_C)\,
Este trabajo es negativo ya que en esta expansión es realmente el sistema el que trabaja sobre el ambiente.
Enfriamiento a volumen constante
Al no desplazarse las paredes del sistema, aquí no se realiza trabajo mecánico
W_{C\to A} = 0\,

Sumando las tres contribuciones obtenemos el trabajo total

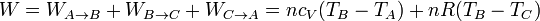
W = W_{A\to B}+W_{B\to C}+W_{C\to A} = nc_V(T_B-T_A)+nR(T_B-T_C)\,

Para ver que este resultado coincide con el que obtuvimos antes, hacemos uso de la ley de Mayer

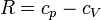
R = c_p-c_V\,   \Rightarrow   W = ncV(TB − TA) + n(cp − cV)(TB − TC) = ncp(TB − TC) + ncV(TC − TA) = − Qc − Qf

2.4 Rendimiento

El rendimiento del ciclo es igual al cociente entre el trabajo neto realizado por el sistema y el calor absorbido durante el ciclo

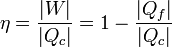
\eta = \frac{|W|}{|Q_c|}=1-\frac{|Q_f|}{|Q_c|}

Sustituyendo las expresiones obtenidas anteriormente

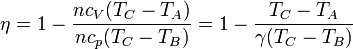
\eta = 1 - \frac{nc_V(T_C-T_A)}{nc_p(T_C-T_B)}=1-\frac{T_C-T_A}{\gamma(T_C-T_B)}

Para expresar el rendimiento en función de la razón de compresión r = VA / VB observamos que, por ser B→C un proceso a presión constante se cumple la ley de Charles

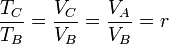
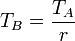
\frac{T_C}{T_B}=\frac{V_C}{V_B}=\frac{V_A}{V_B}=r   \Rightarrow   T_B=\frac{T_A}{r}

En el proceso a volumen constante, la proporcionalidad se da entre la presión y la temperatura

\frac{T_C}{T_A} = \frac{p_C}{p_A}=\frac{p_B}{p_A}

La relación de presiones pB / pA no es independiente de la relación de compresión, sino que están relacionados por la condición de que el proceso A→B es adiabático y reversible

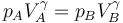
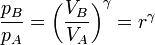
p_AV_A^\gamma = p_BV_B^\gamma\,   \Rightarrow   \frac{p_B}{p_A}=\left(\frac{V_B}{V_A}\right)^\gamma = r^\gamma

Por tanto tenemos la relación

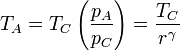
T_A = T_C\left(\frac{p_A}{p_C}\right)=\frac{T_C}{r^\gamma}

Llevando esto a la expresión del rendimiento

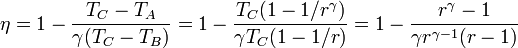
\eta = 1-\frac{T_C-T_A}{\gamma(T_C-T_B)} = 1 - \frac{T_C(1-1/r^\gamma)}{\gamma T_C(1-1/r)}=1-\frac{r^\gamma-1}{\gamma r^{\gamma-1}(r-1)}

Comparando este resultado con el de un ciclo Diesel vemos que esta expresión es idéntica a la que se obtiene para ese ciclo si hacemos la relación de combustión rc igual a la relación de compresión. En realidad, el ciclo descrito en este problema es en realidad un ciclo Diesel ideal, en el cual una de las adiabáticas se ha reducido a un punto.

3 Valores numéricos

Se trata ahora de hallar todos los valores anteriores, y algunos más, para un caso particular, con condiciones

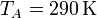
pA = 100,kPa        VA = 1900cm3        T_A=290\,\mathrm{K}

El número de moles de gas, que será una constante en el ciclo, lo obtenemos aplicando la ley de los gases ideales

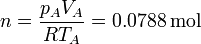
n = \frac{p_AV_A}{RT_A} = 0.0788\,\mathrm{mol}

Por la relación de compresión tenemos el volumen de B; el de C es igual al de A,

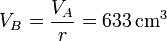
V_B=\frac{V_A}{r}=633\,\mathrm{cm}^3        V_C=V_A=1900\,\mathrm{cm}^3

La presión en B (y C) la obtenemos de la ecuación para una adiabática reversible que obtuvimos antes

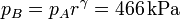
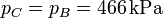
p_B = p_A r^\gamma = 466\,\mathrm{kPa}        p_C=p_B=466\,\mathrm{kPa}

Aquí hemos usado el valor γ = 1.4, propio del aire.

La temperatura en B la hallamos por aplicación de la ley de los gases ideales

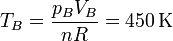
T_B=\frac{p_BV_B}{nR} = 450\,\mathrm{K}

También se puede obtener esta temperatura empleando la relación para un proceso adiabático

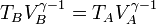
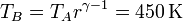
T_BV_B^{\gamma-1}=T_AV_A^{\gamma-1}\,   \Rightarrow   T_B = T_A r^{\gamma-1} = 450\,\mathrm{K}

la temperatura en C la obtenemos de la ley de Charles

T_C = T_B\frac{V_C}{V_B}=T_Br = 1350\,\mathrm{K}

Reuniendo todos estos resultados en una tabla nos queda

{|class="bordeado"

|- ! ! A ! B ! C |- ! p(kPa) | 100 | 466 | 466 |- ! V(cm3) | 1900 | 633 | 1900 |- ! T(K) | 290 | 450 | 1350 |-

|}

4 Entropía

5 Trabajo perdido

Obtenido de "http://tesla.us.es/wiki/index.php/Caso_extremo_de_ciclo_Diesel"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace