Caso extremo de ciclo Diesel
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Enunciado) |
||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | Una máquina térmica funciona según el siguiente proceso: | + | Una máquina térmica funciona funciona con aire (gas ideal) según el siguiente proceso: |
* El gas contenido en una cámara se comprime adiabáticamente de forma reversible desde un volumen máximo <math>V_A</math> hasta un volumen <math>V_B</math>, siendo la razón de compresión <math>r = V_A/V_B</math>. | * El gas contenido en una cámara se comprime adiabáticamente de forma reversible desde un volumen máximo <math>V_A</math> hasta un volumen <math>V_B</math>, siendo la razón de compresión <math>r = V_A/V_B</math>. | ||
| Línea 12: | Línea 12: | ||
<li> Para el caso concreto de aire con <math>p_A=100\,\mathrm{kPa}</math>, <math>t_A=17^\circ\mathrm{C}</math>, <math>V_A=1900\,\mathrm{cm}^3</math> y <math>r=3</math>, ¿cuánto valen las temperaturas y presiones en B y C? ¿Y el calor absorbido, el cedido y el trabajo realizado? ¿Y el rendimiento? </li> | <li> Para el caso concreto de aire con <math>p_A=100\,\mathrm{kPa}</math>, <math>t_A=17^\circ\mathrm{C}</math>, <math>V_A=1900\,\mathrm{cm}^3</math> y <math>r=3</math>, ¿cuánto valen las temperaturas y presiones en B y C? ¿Y el calor absorbido, el cedido y el trabajo realizado? ¿Y el rendimiento? </li> | ||
<li> Supongamos que el calentamiento se produce a base de poner en contacto el gas con un foco a temperatura constante <math>T_C</math>, y el enfriamiento mediante el contacto con el ambiente a <math>T_A</math>. ¿Cuánto vale la variación de entropía en el sistema y en el universo en cada paso? ¿Cuál es la variación neta de entropía del universo?</li> | <li> Supongamos que el calentamiento se produce a base de poner en contacto el gas con un foco a temperatura constante <math>T_C</math>, y el enfriamiento mediante el contacto con el ambiente a <math>T_A</math>. ¿Cuánto vale la variación de entropía en el sistema y en el universo en cada paso? ¿Cuál es la variación neta de entropía del universo?</li> | ||
| - | <li> ¿Cuánto vale el trabajo perdido en este ciclo si lo comparamos con el máximo posible para el mismo calor absorbido?</li> | + | <li> ¿Cuánto vale el trabajo perdido en este ciclo si lo comparamos con el máximo posible para el mismo calor absorbido con las |
| + | temperaturas de trabajo <math>T_A</math> y <math>T_C</math>?</li> | ||
</ol> | </ol> | ||
Revisión de 14:06 15 jun 2009
Contenido |
1 Enunciado
Una máquina térmica funciona funciona con aire (gas ideal) según el siguiente proceso:
- El gas contenido en una cámara se comprime adiabáticamente de forma reversible desde un volumen máximo VA hasta un volumen VB, siendo la razón de compresión r = VA / VB.
- A partir de ahí, el gas se pone en contacto con un foco térmico y se calienta a presión constante hasta un estado C, cuyo volumen es igual al inicial.
- Acto seguido, el gas se enfría a volumen constante hasta que la temperatura retorna a su valor inicial.
- Halle el calor absorbido y cedido por el gas durante el ciclo, así como el trabajo realizado sobre el sistema. Demuestre que el rendimiento de este ciclo es igual a
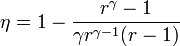
- Para el caso concreto de aire con
, 
, 
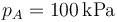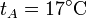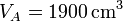y r = 3, ¿cuánto valen las temperaturas y presiones en B y C? ¿Y el calor absorbido, el cedido y el trabajo realizado? ¿Y el rendimiento? - Supongamos que el calentamiento se produce a base de poner en contacto el gas con un foco a temperatura constante TC, y el enfriamiento mediante el contacto con el ambiente a TA. ¿Cuánto vale la variación de entropía en el sistema y en el universo en cada paso? ¿Cuál es la variación neta de entropía del universo?
- ¿Cuánto vale el trabajo perdido en este ciclo si lo comparamos con el máximo posible para el mismo calor absorbido con las temperaturas de trabajo TA y TC?
