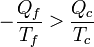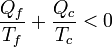Desigualdad de Clausius
De Laplace
(→Ciclo irreversible) |
(→Máquina térmica) |
||
| Línea 63: | Línea 63: | ||
El significado físico de este resultado es simple: a igualdad de temperaturas y para el mismo calor tomado del foco caliente, la máquina irreversible produce una cantidad mayor de calor de desecho <math>|Q_f|</math> que una reversible | El significado físico de este resultado es simple: a igualdad de temperaturas y para el mismo calor tomado del foco caliente, la máquina irreversible produce una cantidad mayor de calor de desecho <math>|Q_f|</math> que una reversible | ||
| + | |||
| + | Teniendo en cuenta de nuevo que <math>Q_f</math> es negativo queda, finalmente | ||
| + | |||
| + | <math>|Q_f| = -Q_f</math>{{tose}}<math>-\frac{Q_f}{T_f}>\frac{Q_c}{T_c}</math>{{tose}}<math>\frac{Q_f}{T_f}+\frac{Q_c}{T_c} < 0</math> | ||
==Enunciado general== | ==Enunciado general== | ||
Revisión de 17:15 6 may 2009
Contenido |
1 Introducción
Al introducir el Segundo Principio de la termodinámica, se formulan varios enunciados que, aunque poseen validez general, están expresados en términos de máquinas térmicas. Los más importantes de estos enunciados son:
- Enunciado de Kelvin-Planck
- No puede construirse un dispositivo que, operando en un ciclo, tenga como único resultado la absorción de calor de un solo foco y la producción de una cantidad equivalente de trabajo.
- Enunciado de Clausius
- Es imposible construir un dispositivo que, operando cíclicamente, tenga como único resultado el paso de calor de un foco frío a uno caliente.
- Teorema de Carnot
- El rendimiento de una máquina térmica irreversible que funcione entre dos temperaturas es siempre menor que el de una máquina térmica reversible que funcione entre las mismas temperaturas.
Estos tres enunciados son bastante “concretos” en cuanto a que hablan de procesos y dispositivos fácilmente interpretables. No obstante, el segundo principio de la termodinámica puede enunciarse de formas más abstracta que, si bien requieren un mayor esfuerzo para su interpretación, ponen de manifiesto de forma más clara la validez universal de esta ley.
Uno de estos enunciados, que es el que se trata en este artículo es la
- Desigualdad de Clausius
- Para todo proceso cíclico
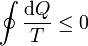
- cumpliéndose la desigualdad si el proceso es irreversible, y la igualdad si es reversible.
2 El caso de dos focos térmicos
Antes de enunciar de forma completa y rigurosa la desigualdad de Clausius, conviene presentar y analizar el caso más simple y importante de un sistema en contacto con solo dos focos de temperatura, uno caliente a temperatura Tc y uno frío a Tf.
Desde el foco caliente entrará en el sistema una cierta cantidad de calor Qc y desde el foco frío una cantidad Qf. Evidentemente, una de estas dos, o las dos, cantidades será negativa, queriendo decir con ello que el sistema cede calor bien al foco frío (caso de una máquina térmica normal), bien al foco caliente (caso de un refrigerador o de una bomba de calor).
Sobre el sistema se realiza una cierta cantidad de trabajo W que puede ser positivo (caso de un refrigerador o una bomba de calor) o negativo (caso de una máquina térmica).
2.1 Ciclo reversible
Por el corolario al teorema de Carnot se tiene que todas las máquinas reversibles que operen entre las mismas temperaturas tienen el mismo rendimiento. Como todas tienen el mismo puede calcularse analizando algún caso particular, siendo el más sencillo el ciclo de Carnot. El resultado es que
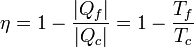
Restando cada miembro de la unidad queda la igualdad equivalente
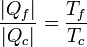
o, equivalentemente,
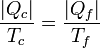
Es decir que la cantidad de calor que toma o cede de una fuente es proporcional a la temperatura de dicha fuente.
En el caso de una máquina térmica, Qc es positivo, pero el calor Qf es negativo, por lo que
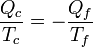
o, lo que es lo mismo,
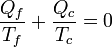(ciclo reversible)En el caso de un refrigerador o de una bomba de calor la cantidad negativa es Qc, pero el resultado final es el mismo.
2.2 Ciclo irreversible
2.2.1 Máquina térmica
Consideremos un proceso cíclico irreversible que toma calor Qc de un foco caliente a temperatura Tc y cede una cantidad | Qf | a un foco frío a temperatura Tf.
De acuerdo con el teorema de Carnot, el rendimiento de esta máquina térmica será menor que el de una reversible que trabaje entre las mismas dos temperaturas. Esto implica
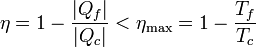
Despejando llegamos a la relación
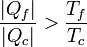
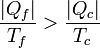
El significado físico de este resultado es simple: a igualdad de temperaturas y para el mismo calor tomado del foco caliente, la máquina irreversible produce una cantidad mayor de calor de desecho | Qf | que una reversible
Teniendo en cuenta de nuevo que Qf es negativo queda, finalmente
| Qf | = − Qf 
