Campo producido por una espira poligonal
De Laplace
(Diferencias entre revisiones)
(Nueva página: ==Enunciado== Por las espira de formas irregulares de las figuras circula una corriente <math>I</math>. Halle el valor del campo en el punto <math>P</math> en cada caso. <center>[[Im...) |
(→Campo en P) |
||
| Línea 8: | Línea 8: | ||
==Cuadrilátero== | ==Cuadrilátero== | ||
===Campo en P=== | ===Campo en P=== | ||
| - | El campo es la suma de las contribuciones de cada uno de los lados del cuadrilátero. | + | El campo es la suma de las contribuciones de cada uno de los lados del cuadrilátero. El [[Campo_magnético_de_una_corriente_rectilínea|campo de un segmento]] puede calcularse por integración directa, resultando la expresión |
| + | |||
| + | <center><math>\mathbf{B}=\frac{\mu_0 I}{4\pi\rho}(\,\mathrm{sen}\,\alpha_2-\,\mathrm{sen}\,\alpha_1)\mathbf{n}</math></center> | ||
| + | |||
| + | El punto P se encuentra en la intersección de la prolongación de | ||
| - | |||
===Momento magnético=== | ===Momento magnético=== | ||
==Espira alabeada== | ==Espira alabeada== | ||
Revisión de 10:38 20 abr 2009
Contenido |
1 Enunciado
Por las espira de formas irregulares de las figuras circula una corriente I. Halle el valor del campo en el punto P en cada caso.
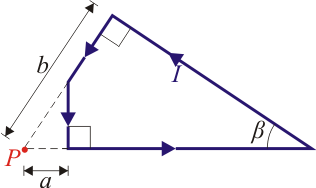
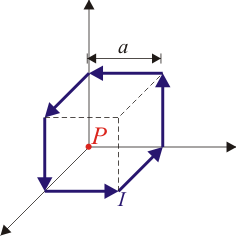
Para cada una de las espiras, hállese su momento magnético y la expresión del campo magnético y del potencial vector en puntos alejados de la espira.
2 Cuadrilátero
2.1 Campo en P
El campo es la suma de las contribuciones de cada uno de los lados del cuadrilátero. El campo de un segmento puede calcularse por integración directa, resultando la expresión
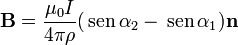
El punto P se encuentra en la intersección de la prolongación de





